In triangles ABC and DEF , ∠A=∠E=40o , AB:ED=AC:EF and ∠F=65o , then ∠B= 35o (b) 65o (c) 75o (d) 85o
To solve the problem, we need to find the value of angle B in triangle ABC given the information about triangles ABC and DEF.
1. Identify the Given Information:
- Angle A = Angle E = 40°
- Sides AB = ED and AC = EF
- Angle F = 65°
2. Establish Triangle Similarity:
- Since we have two pairs of sides that are equal (AB = ED and AC = EF) and the included angle (Angle A = Angle E) is the same, we can use the Side-Angle-Side (SAS) similarity criterion.
- Therefore, triangle ABC is similar to triangle DEF.
3. Corresponding Angles in Similar Triangles:
- From the similarity of the triangles, we know that corresponding angles are equal:
- Angle A = Angle E = 40°
- Angle B = Angle D
- Angle C = Angle F
4. Use the Given Angle F:
- We know that Angle F = 65°. Therefore, Angle C = 65°.
5. Apply the Triangle Sum Property:
- In triangle ABC, the sum of the angles must equal 180°:
Angle A+Angle B+Angle C=180°
Substituting the known values:
40°+Angle B+65°=180°
6. Solve for Angle B:
- Combine the known angles:
105°+Angle B=180°
- Isolate Angle B:
Angle B=180°−105°=75°
Final Answer:
Angle B = 75°.
- Angle A = Angle E = 40°
- Sides AB = ED and AC = EF
- Angle F = 65°
- Since we have two pairs of sides that are equal (AB = ED and AC = EF) and the included angle (Angle A = Angle E) is the same, we can use the Side-Angle-Side (SAS) similarity criterion.
- Therefore, triangle ABC is similar to triangle DEF.
- From the similarity of the triangles, we know that corresponding angles are equal:
- Angle A = Angle E = 40°
- Angle B = Angle D
- Angle C = Angle F
- We know that Angle F = 65°. Therefore, Angle C = 65°.
- In triangle ABC, the sum of the angles must equal 180°:
Angle A+Angle B+Angle C=180°
Substituting the known values:
40°+Angle B+65°=180°
- Combine the known angles:
105°+Angle B=180°
- Isolate Angle B:
Angle B=180°−105°=75°
Angle B = 75°.
Topper's Solved these Questions
Similar Questions
In triangles ABC and DEF , ∠A=∠E=40o , AB:ED=AC:EF and ∠F=65o , then ∠B= 35o (b) 65o (c) 75o (d) 85o
View SolutionTwo triangles ABC and DEF such that ∠A=∠D,∠B=∠Eand∠C=∠F. Then
View SolutionIf ABC and DEF are similar triangles such that ∠A=47o and ∠E=83o , then ∠C= 50o (b) 60o (c) 70o (d) 80o
View SolutionIf in two triangles ABC and DEF , ABDE=BCFE=CAFD , then FDECAB (b) FDEABC (c) CBAFDE (d) BCAFDE
View SolutionIf in two triangles ABC and DEF , ∠A=∠E, ∠B=∠F , then which of the following is not true? BCDF=ACDE (b) ABDE=BCDF (c) ABEF=ACDE (d) BCDF=ABEF
View SolutionIn Fig. 71, if ABCD and CDEF, find ∠ACE
View SolutionIn Figure, if EC∣∣AB, ∠ECD=700AND ∠BDO=200 , then ∠OBD is: 200 (b) 500 (c) 600 (d) 700
View SolutionIn Figure, AB⊥BEandFE⊥BE.If BC=DEandAB=EF, then ABD is congruent to:
(a)EFC
(b) ECF
(c) CEF
(d) FEC
View SolutionIf ABC and DEF are two triangles such that ABDE=BCEF=CAFD=25 , then Area(ABC):Area(DEF)= 2:5 (b) 4:25 (c) 4:15 (d) 8:125
View SolutionIn figure, ΔODCΔOBA,∠BOC=125oand ∠CDO=70o. Find∠DOC,∠DCOand∠OAB.
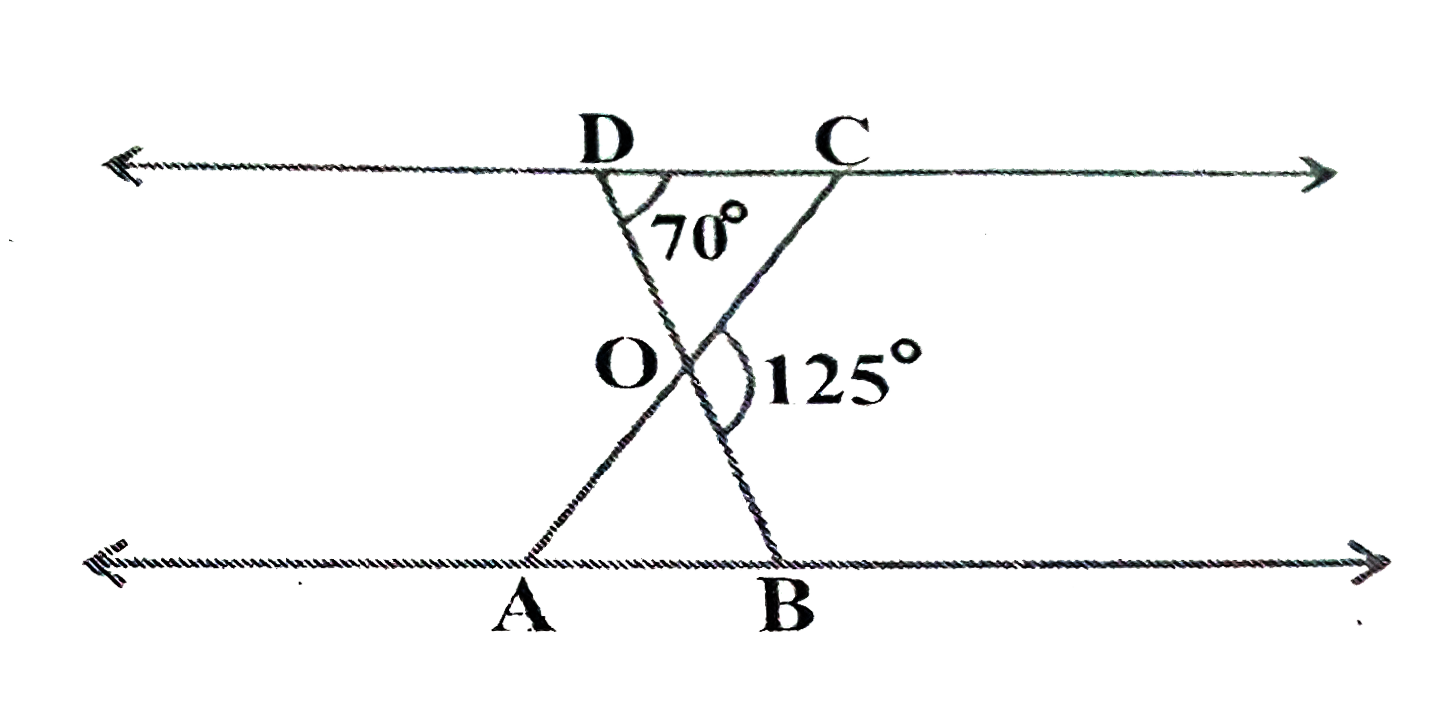
View Solution
