In Figure, O is the centre of the circle of radius 5 cm.OP⊥AB, OQ⊥CD, ABCD, AB=6 cm and CD=8 cm. Determine PQ
To solve the problem, we need to determine the length of PQ given the following information:
- O is the center of the circle with a radius of 5cm.
- OP⊥AB and OQ⊥CD.
- AB and CD are parallel lines.
- The lengths of AB and CD are 6cm and 8cm respectively.
1. Identify the lengths of segments:
- Since OP is perpendicular to AB, it bisects AB. Therefore, the length of AP is:
AP=AB2=6cm2=3cm
- Similarly, since OQ is perpendicular to CD, it bisects CD. Therefore, the length of CQ is:
CQ=CD2=8cm2=4cm
2. Apply the Pythagorean theorem in triangle OAP:
- In triangle OAP, we have:
OA2=OP2+AP2
- Here, OA=5cm (the radius) and AP=3cm. Substituting these values gives:
52=OP2+32
25=OP2+9
OP2=25−9=16
OP=√16=4cm
3. Apply the Pythagorean theorem in triangle OQC:
- In triangle OQC, we have:
OC2=OQ2+CQ2
- Again, OC=5cm and CQ=4cm. Substituting these values gives:
52=OQ2+42
25=OQ2+16
OQ2=25−16=9
OQ=√9=3cm
4. Calculate PQ:
- Now that we have OP and OQ, we can find PQ:
PQ=OP+OQ=4cm+3cm=7cm
Final Answer:
Thus, the length of PQ is 7cm.
---
- OP⊥AB and OQ⊥CD.
- AB and CD are parallel lines.
- The lengths of AB and CD are 6cm and 8cm respectively.
- Since OP is perpendicular to AB, it bisects AB. Therefore, the length of AP is:
AP=AB2=6cm2=3cm
- Similarly, since OQ is perpendicular to CD, it bisects CD. Therefore, the length of CQ is:
CQ=CD2=8cm2=4cm
- In triangle OAP, we have:
OA2=OP2+AP2
- Here, OA=5cm (the radius) and AP=3cm. Substituting these values gives:
52=OP2+32
25=OP2+9
OP2=25−9=16
OP=√16=4cm
- In triangle OQC, we have:
OC2=OQ2+CQ2
- Again, OC=5cm and CQ=4cm. Substituting these values gives:
52=OQ2+42
25=OQ2+16
OQ2=25−16=9
OQ=√9=3cm
- Now that we have OP and OQ, we can find PQ:
PQ=OP+OQ=4cm+3cm=7cm
Thus, the length of PQ is 7cm.
Topper's Solved these Questions
Similar Questions
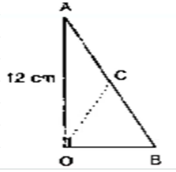
In Figure, ∠AOB=900, AC=BC, OA=12 cm and OC=6.5cm. Find the area of AOB.
View SolutionIn Figure, ABCD is a quadrilateral in which diagonal AC=84 cm ; DL⊥AC, BM⊥AC, DL=16.5 cm and BM=12 cm . Find the area of quadrilateral ABCD.
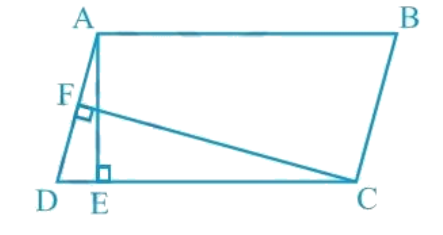
View SolutionIn Figure, ABCD is a parallelogram, AE ⊥DC and CF⊥AD . If AB=16CM, AE=8cm and CF=10cm, find AD
View SolutionWhich of the following pairs of triangles are congruent? If they are congruent, write out the pairs of equal angles. ABC:AB=3cm, BC=4cm, CA=2 cm DEF:DE=2 cm, EF=3 cm and FD=4 cm PQR:PQ=17 cm, QR=15 cm, PR=18 cm DEF:DE=18 cm, EF=17 cm, DF=15 cm .
View SolutionPQ and RS are two parallel chords of a circle whose centre is O and radius is 10 cm. If PQ=16 cm and RS=12 cm, find the distance between PQ and RS, if they lie: on opposite side of the centre O
View SolutionPQ and RS are two parallel chords of a circle whose centre is O and radius is 10 cm. If PQ=16 cm and RS=12 cm, find the distance between PQ and RS, if they lie: on the same side of centre O
View SolutionAB and CD are two chords of a circle such that AB=6 cm, CD=12 cm and ABCD. If the distance between AB and CD is 3 cm, find the radius of the circle.
View SolutionIn Fig. 4.230, each of PA, QB, RC and SD is perpendicular to l . If AB=6cm , BC=9cm , CD=12cm and PS=36cm , then determine PQ, QR and RS . (FIGURE)
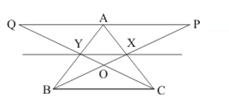
View SolutionIn Figure, XandY are the mid-points of ACandAB respectively, QP,BCandCYQandBXP are straight lines. Prove that ar(ABP)=ar(ACQ)
View SolutionIn a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC=21 cm, BC=29cm and AB=30cm, find the perimeter of the quadrilateral ARPQ
View Solution
