In Figure, ∠A=600 and ∠ABC=800, find ∠DPC and ∠BQC
To solve the problem step by step, we will find the angles ∠DPC and ∠BQC using the given angles ∠A=60∘ and ∠ABC=80∘.
Step 1: Find ∠ABC
We know that ∠A=60∘ and ∠ABC=80∘.
Step 2: Find ∠ACB
In triangle ABC, the sum of the angles is 180∘. Therefore, we can write:
∠A+∠ABC+∠ACB=180∘
Substituting the known values:
60∘+80∘+∠ACB=180∘
140∘+∠ACB=180∘
∠ACB=180∘−140∘=40∘
Step 3: Use the property of cyclic quadrilaterals
Since ABCD is a cyclic quadrilateral, we know that the opposite angles sum up to 180∘. Therefore:
∠ABC+∠ADC=180∘
Substituting the known value of ∠ABC:
80∘+∠ADC=180∘
∠ADC=180∘−80∘=100∘
Step 4: Find ∠DPC
In triangle ADP, we again apply the angle sum property:
∠A+∠D+∠DPC=180∘
Substituting the known values:
60∘+100∘+∠DPC=180∘
160∘+∠DPC=180∘
∠DPC=180∘−160∘=20∘
Step 5: Find ∠BQC
Now, we will find ∠BQC using triangle BQC:
∠ABC+∠BQC+∠ACB=180∘
Substituting the known values:
80∘+∠BQC+40∘=180∘
120∘+∠BQC=180∘
∠BQC=180∘−120∘=60∘
Final Answers:
- ∠DPC=20∘
- ∠BQC=60∘
We know that ∠A=60∘ and ∠ABC=80∘.
In triangle ABC, the sum of the angles is 180∘. Therefore, we can write:
∠A+∠ABC+∠ACB=180∘
Substituting the known values:
60∘+80∘+∠ACB=180∘
140∘+∠ACB=180∘
∠ACB=180∘−140∘=40∘
Since ABCD is a cyclic quadrilateral, we know that the opposite angles sum up to 180∘. Therefore:
∠ABC+∠ADC=180∘
Substituting the known value of ∠ABC:
80∘+∠ADC=180∘
∠ADC=180∘−80∘=100∘
In triangle ADP, we again apply the angle sum property:
∠A+∠D+∠DPC=180∘
Substituting the known values:
60∘+100∘+∠DPC=180∘
160∘+∠DPC=180∘
∠DPC=180∘−160∘=20∘
Now, we will find ∠BQC using triangle BQC:
∠ABC+∠BQC+∠ACB=180∘
Substituting the known values:
80∘+∠BQC+40∘=180∘
120∘+∠BQC=180∘
∠BQC=180∘−120∘=60∘
- ∠DPC=20∘
- ∠BQC=60∘
Topper's Solved these Questions
Similar Questions
ABCD is a cyclic quadrilateral in which: BCAD, ∠ADC=1100 and ∠BAC=500. Find ∠DAC ∠DBC=800 and ∠BAC=400. Find ∠BCD ∠BCD=1000and ∠ABD=700 find ∠ADB
View SolutionIn a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC=300, ∠BDC=100and ∠CAB=700, Find: ∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB
Given that
∠ABC=302,∠ABC=∠ADC=300
[We know that measure of opposite angles are equal in a parallelogram]
∠BDC=100
∠CAB=700
∠BDA=∠ADB=∠ADC–∠BDC
302–102=202
∠DAB=1800–300=1500
∠ADB=∠DBC=200 (alternate angles)
∠BCD=∠DAB=1500
[we know, opposite angles are equal in a parallelogram]
∠DBA=∠BDC=100
[we know, Alternate interior angles are equal]
InΔABC
∠CAB+∠ABC+∠BCA=1800
[since, sum of all angles of a triangle is 180^0]
700+300+∠BCA=1800
∠BCA=1800–1000=800
∠DAB=∠DAC+∠CAB=700+800=1500
∠BCD=1500 (opposite angle of the parallelogram)
∠DCA=∠CAB=700
In ΔDOC∠BDC+∠ACD+∠DOC=1800
[since, sum of all angles of a triangle is 180^0]
100+700+∠DOC=1800
∠DOC=1800−800
∠ACB=800
View SolutionIn Fig.81, side BC of ABC has been produced to D and CEBA. If ∠ABC=650, ∠BAC=550, find ∠ACE, ∠ECD and ∠ACD.
View SolutionIn Fig.103, PQRS and ∠PAB=600 and ∠ACS=1000. Then, ∠BAC= (a) (b)(c)(d)(e)40(f)0(g)(h)(i) (j) (b) (k)(l)(m)(n)60(o)0(p)(q)(r) (s) (c) (d)(e)(f)(g)80(h)0(i)(j)(k) (l) (d) (m)(n)(o)(p)50(q)0(r)(s)(t) (u)
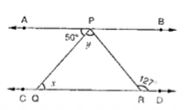
View SolutionIn Figure, if AB∣∣CD, ∠APQ=500AND ∠PRD=1270, find x and y
View SolutionIn Figure, PQ∣∣RS, ∠AEF=950, ∠BHS=1100 and ∠ABC=x0. Then the value of x is (a)150 (b) 250 (c) 700 (d) 350
View SolutionIn a parallelogram ABCD , if ∠DAB=75∘and ∠DBC=60∘, then ∠BDC=(a) 75∘ (b) 60∘ (c) 45∘ (d) 55∘
View SolutionIn Fig. 71, if ABCD and CDEF, find ∠ACE
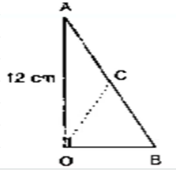
View SolutionIn Figure, ∠AOB=900, AC=BC, OA=12 cm and OC=6.5cm. Find the area of AOB.
View SolutionIn Fig.104, ABCD, ∠OAB=1500 and ∠OCD=1200. Then, ∠AOC= (a) (b)(c)(d)(e)80(f)0(g)(h)(i) (j) (b) (k)(l)(m)(n)90(o)0(p)(q)(r) (s) (c) (d)(e)(f)(g)70(h)0(i)(j)(k) (l) (d) (m)(n)(o)(p)100(q)0(r)(s)(t) (u)
View Solution
