If AD is the median of △ABC, using vectors, prove that AB2+AC2=2(AD2+CD2)
Given that,
AD
is the median of △ABC,
−−→AB=→b
−−→AC=→c
−−→AD=→b+→c2
LHS=AB2+AC2
=∣∣→AB∣∣2+∣∣→AC∣∣2
=b2+c2
−−→CD=→b+→c2−→c=→b−→c2
RHS=2(AD2+CD2)
=2⎡⎣∣∣∣→b+→c2∣∣∣2+∣∣∣→b−→c2∣∣∣2⎤⎦
=24[∣∣→b+→c∣∣2+∣∣→b−→c∣∣2]
=12[∣∣→b∣∣2+|→c|2+2→b→c+∣∣→b∣∣2+|→c|2−2→b→c]
=2(∣∣→b∣∣2+|→c|2)2
=b2+c2
∴AB2+AC2=2(AD2+CD2)
Topper's Solved these Questions
Similar Questions
In ABC , AD is a median. Prove that AB2+AC2=2 AD2+2 DC2 .
View SolutionIf AD is a median of a triangle ABC, then prove that triangles ADB and ADC are equal in area. If G is the mid-point of median AD, prove that ar (BGC)=2ar ( AGC)
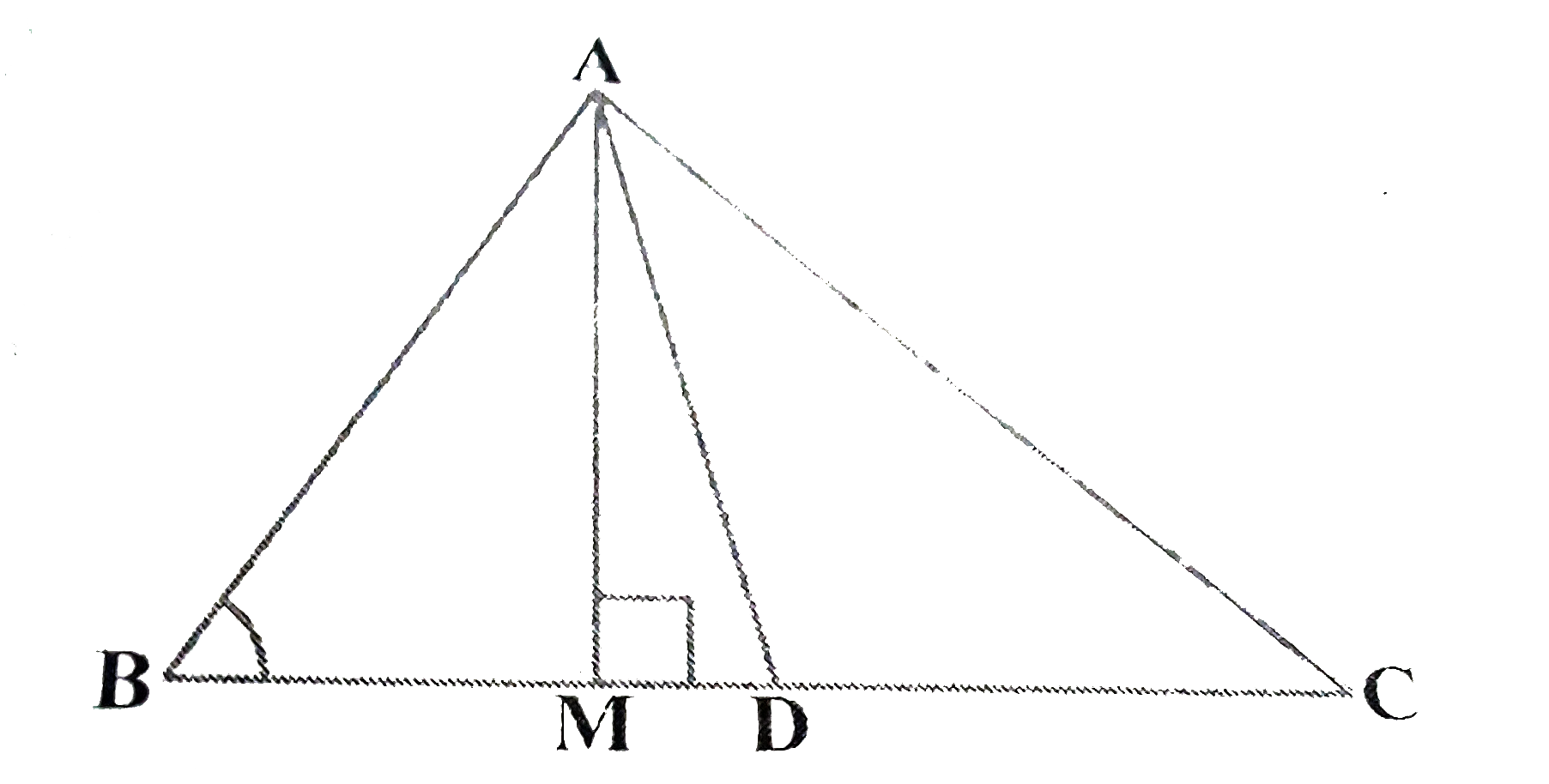
View SolutionIn figure, AD is a median of a triangle ABC and AM⊥BC. Prove that:
(i) AC2=AD2+BC.DM+(BC2)2
(ii) AB2=AD2−BC.DM+(BC2)2
(iii) AC2+AB2=2AD2+12BC2
 View Solution
View SolutionIn a quadrilateral ABCD , given that ∠A+∠D=90o . Prove that AC2+BD2=AD2+BC2 .
View SolutionIn figure, ABC is a triangle in which ∠ABC=90∘and AD⊥BC. Prove that AC2=AB2+BC2−2BC.BD.
 View Solution
View SolutionIn an equilateral triangle ABC if AD⊥BC, then AD2 = (a)CD2 (b) 2CD2 (c) 3CD2 (d) 4CD2
View SolutionIn figure, ABC is triangle in which ∠ABC=90∘and AD⊥CBproduced. Prove that AC2=AB2+BC2−2BC.BD.
 View Solution
View SolutionA point D is taken on the side BC of a ABC such that BD=2dC. Prove that ar(ABD)=2ar(ADC).
View SolutionIf AD,BEandCF are the medians of a ΔABC,then(AD2+BE2+CF2):(BC2+CA2+AB2) is equal to
View SolutionLet AD be a median of the ABC. If AEandAF are medians of the triangle ABDandADC , respectively, and AD=m1,AE=m2,AF=m3, thena28 is equal to (a)m22+m23−2m21 (b) m21+m22−2m23 (c)m21+m23−2m22 (d) none of these
View Solution

