A thin rod of length 'b' is suspended horizontally using ideal strings tied to both ends of the rod. The length of the strings is 'a'. The rod is given an initial angular speed ω its central axis. Let δy be the upwards displacement of rod's centre in a small time interval δ and δF be th total increment in the tension forces just after the rod was given the angular speed.

∂ay=b28a(ωδt)2
δy=b22a(ωδt)
δF=mb24aω2
δF=mb2ω28a
The correct Answer is:A, C
δy=a(1−cosθ)=aθ22
and θa=bϕ2
⇒δy=a2(bϕ2)2=b28aϕ2
⇒δy=b28a(ωδt)2
acc. of rod's centre =b24aω2
⇒δF=mb24aω2

Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
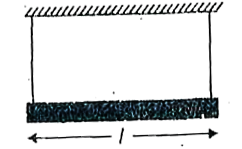
A uniform rod of mass and length l is suspended by two strings at its ends shown. When one of the strings is cut, the rod starts falling with an initial angular acceleration.
View SolutionA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in the figure. When string is cut, the initial angular accleration of the rod is.

View Solution
Knowledge Check
A uniform rod of mass and length l is suspended by two strings at its ends shown. When one of the strings is cut, the rod starts falling with an initial angular acceleration.
 AglBg2lC3g2lD3g4l
AglBg2lC3g2lD3g4lA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in the figure. When string is cut, the initial angular accleration of the rod is.
 A3g2LBgLC2gLD2g3L
A3g2LBgLC2gLD2g3LA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the intial angular acceleration of the rod is
 A3g2LBgLC2gLD2g3L
A3g2LBgLC2gLD2g3L
A rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a masseless string tied to point Q as shown in Fig. When string is cut, the initial angular acceleration of the rod is :

View SolutionA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the intial angular acceleration of the rod is

View SolutionA uniform rod of mass m and length l is pivoted smoothly at O. A horizontal force acts at the bottom of the rod.
a. Find the angular velocity of the rod as the function of angle of rotation θ.
b.What is the maximum angular displacement of the rod?
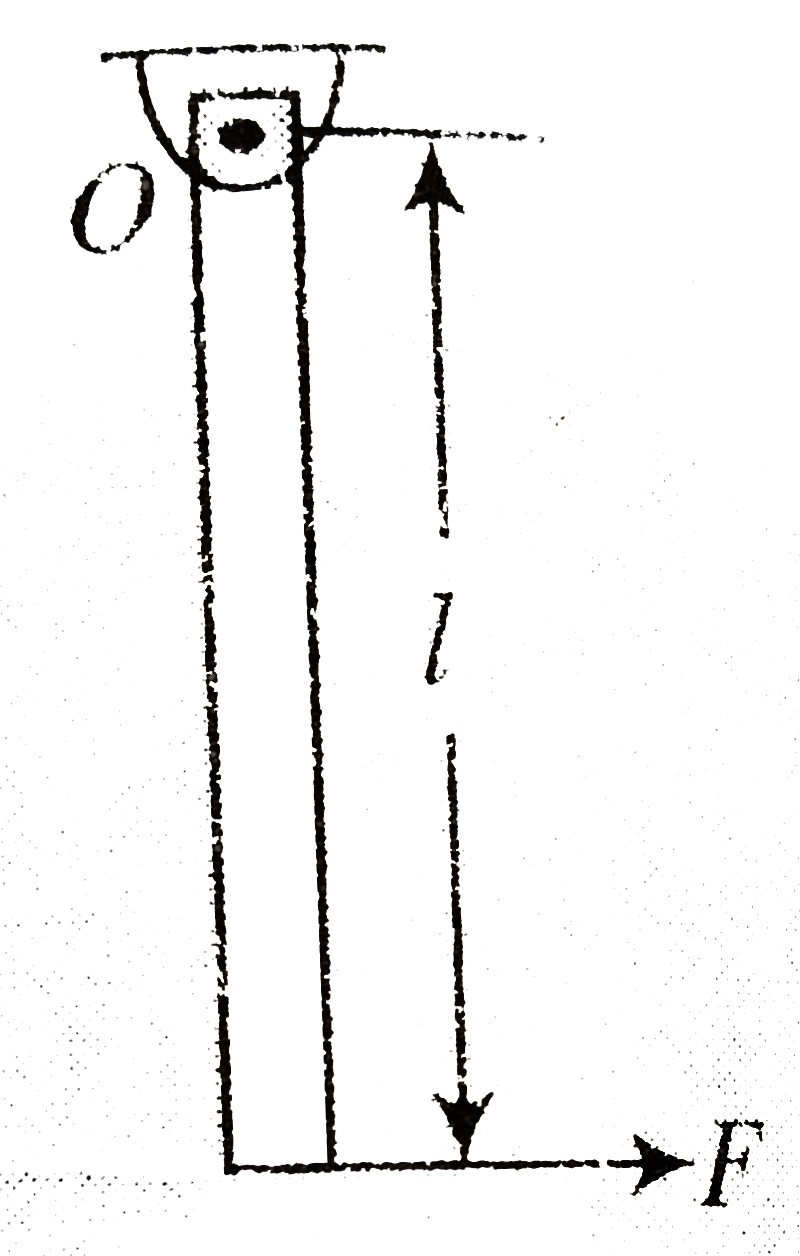
View SolutionA uniform rod of mass m and length l is pivoted smoothly at O. A horizontal force acts at the bottom of the rod.
a. Find the angular velocity of the rod as the function of angle of rotation θ.
b.What is the maximum angular displacement of the rod?
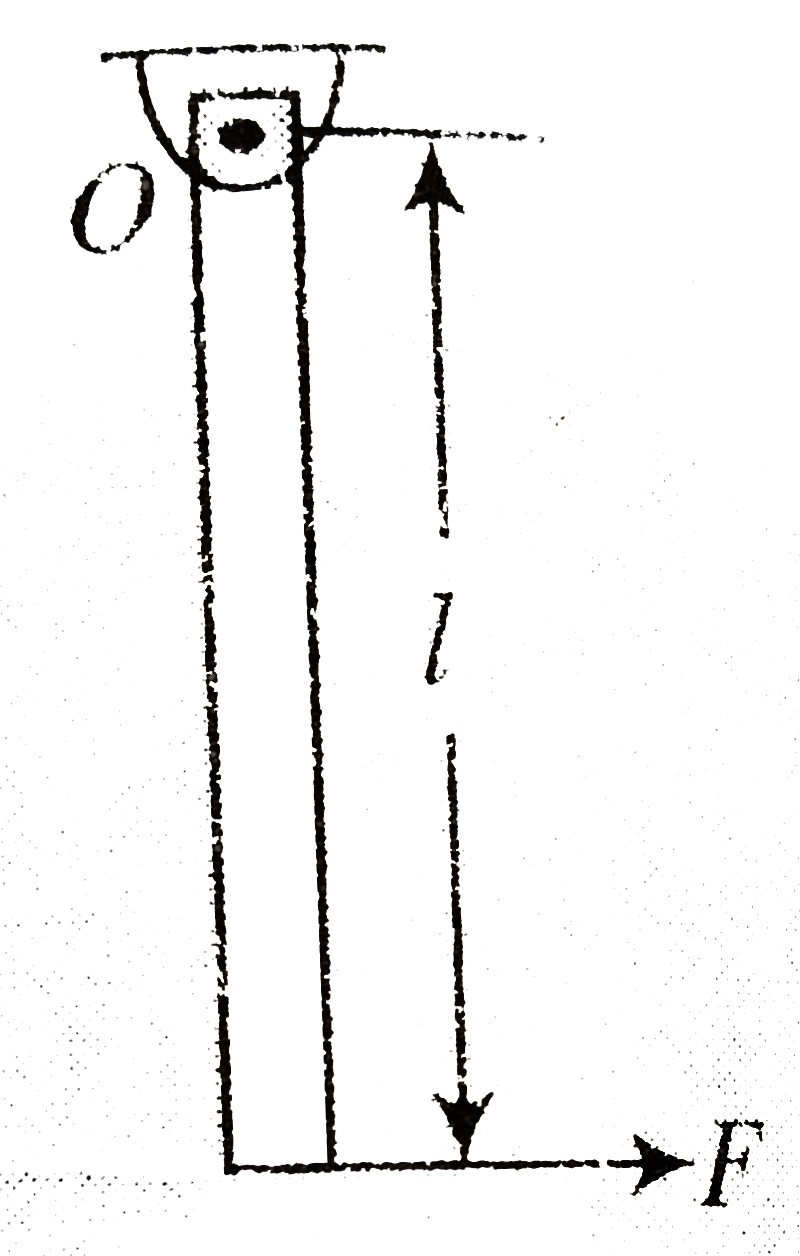
View SolutionA uniform thin rod of length 2L and mass m lies on a horizontal table. A horizontal impulse J is given to the rod at one red. There is no friction. The total kinetic energy of the rod just after the impulse will be
View Solution
