An infinite non-conducting plane with uniform charge density σ is kept parallel to yz plane and at a distance 'd' from a dipole →p which itself is located at the origin. An equipotential surface for this system is spherical, centred at origin, having radius R(<d). Given that R=(pnπσ)1/3, find the integer n

The correct Answer is:2
Tangential components must cancel.
⇒σ2ε0=14πε0psinθR3
⇒R3=p2πσ
⇒n=2

Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
There is an infinite non conducting sheet of charge having uniform charge density σ. The electric field at a point P at a distance x from the sheet is E0. Point O is the foot of the perpendicular drawn from point P on the sheet. A circular portio of radius r<<x centered at O is removed from the sheet. Now the field at point P becomes E0−ΔE. Find ΔE.
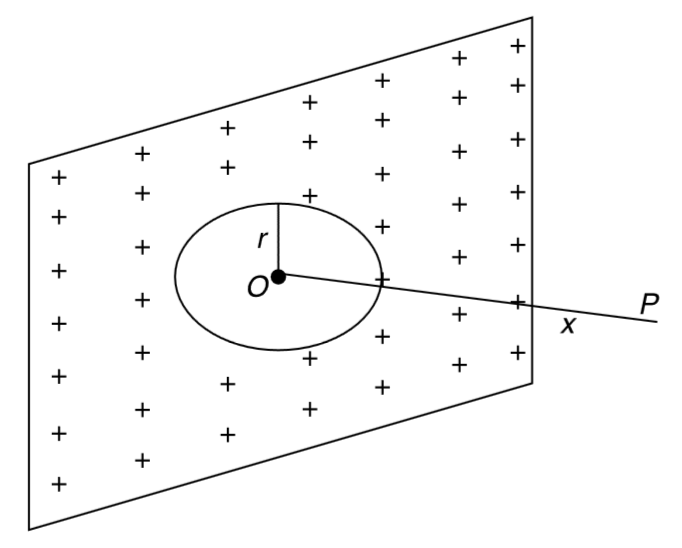
View SolutionAn infinitely large non-conducting plane of uniform surface charge density σ has circular aperture of certain radius carved out from it. The electric field at a point which is at a distance 'a' from the centre of the aperture (perpendicular to the plane) is σ2√2∈0. Find the radius of aperture :
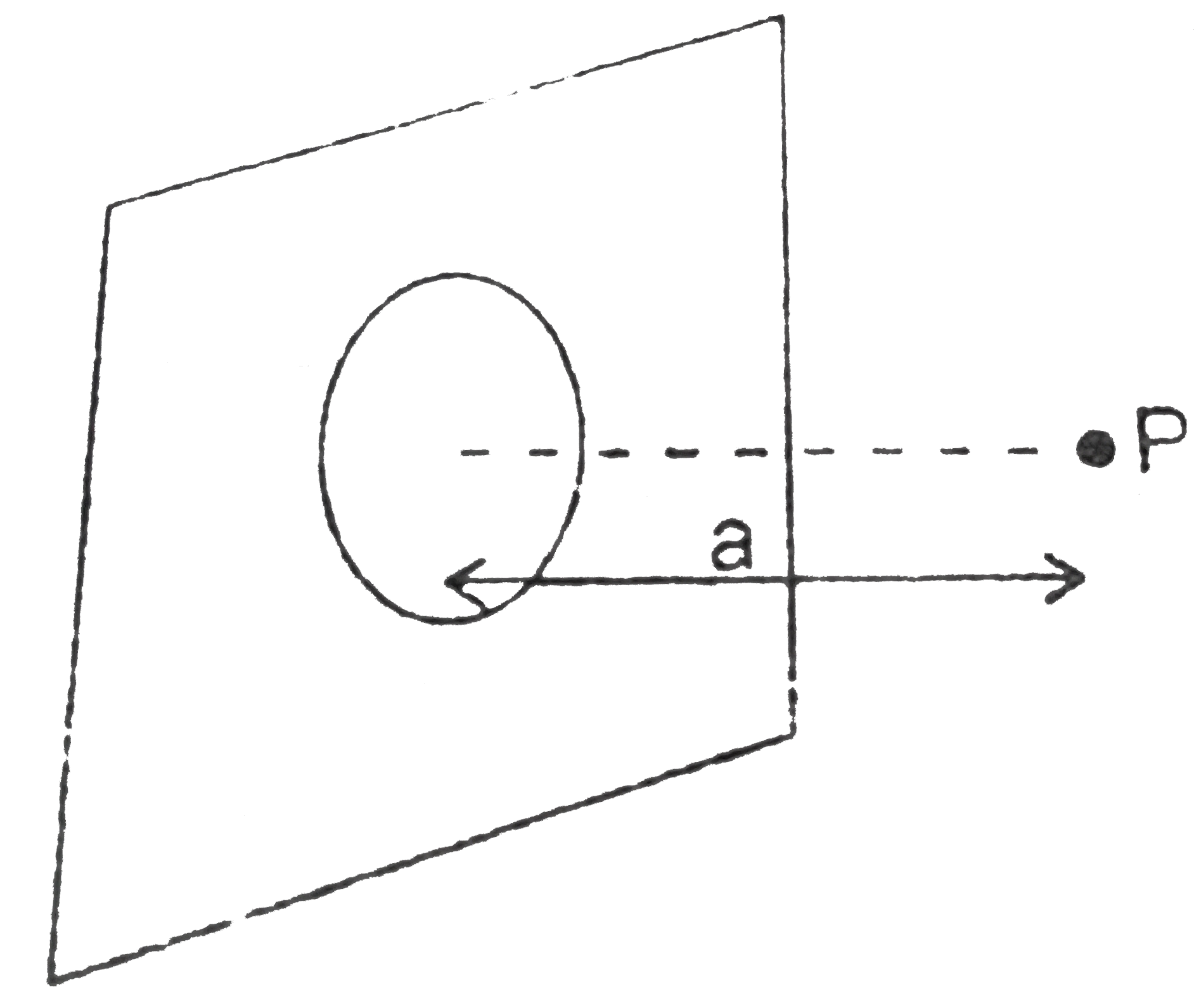
View Solution
Knowledge Check
There is a plane of uniform positive charge density o parallel to the yz-plane and located at x = 2d. A point charge q+ is placed at the origin. Solve for the position x along the x-axis, where a positive test charge will have a net force of zero.
 Ax=√q2πεσBNo solutionCx=√2πσdDx=−2d
Ax=√q2πεσBNo solutionCx=√2πσdDx=−2dConsider a thin spherical shell of radius R consisting of uniform surface charge density σ. The electric field at a point of distance x from its centre and outside the shell is
Ainversely proportional to σBdirectly proportional to x2Cdirectlr proportional to RDinversely proportional to x2Consider a thin spherical shell of radius R consisting of uniform surface charge density σ. The electric field at a point of distance x from its centre and outside the shell is
Ainversely proportional to σBdirectly proportional to x2Cdirectlr proportional to RDinversely proportional to x2
An infinitely large non-conducting plane of uniform surface charge density σ has circular aperture of certain radius carved out from it. The electric field at a point which is at a distance 'a' from the centre of the aperture (perpendicular to the plane) is σ2√2∈0. Find the radius of aperture :

View SolutionAn infinite dielectric sheet having charge density σ has a hole of radius R in it. An electron is released on the axis of the hole at a distance √3R from the center. Find the speed with which it crosses the center of the hole.

View SolutionAn infinite dielectric sheet having charge density σ has a hole of radius R in it. An electron is released on the axis of the hole at a distance √3R from the center. Find the speed with which it crosses the center of the hole.

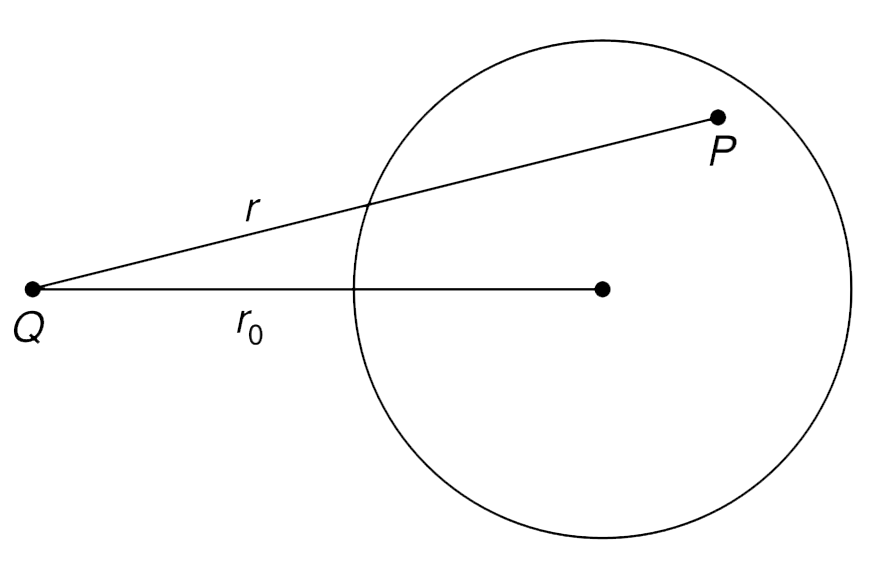
View SolutionA conducting shell having no charge has radius R. A point charge Q is placed in front of it at a distance r0 from its centre. Find potential due to charge induced on the surface of the shell at a point P inside the shell. Distance of point P from point charge Q is r.
View SolutionA uniformly charged disc of radius R having surface charge density σ is placed in the xy plane with its center at the origin. Find the electric field intensity along the z-axis at a distance Z from origin :
View Solution
