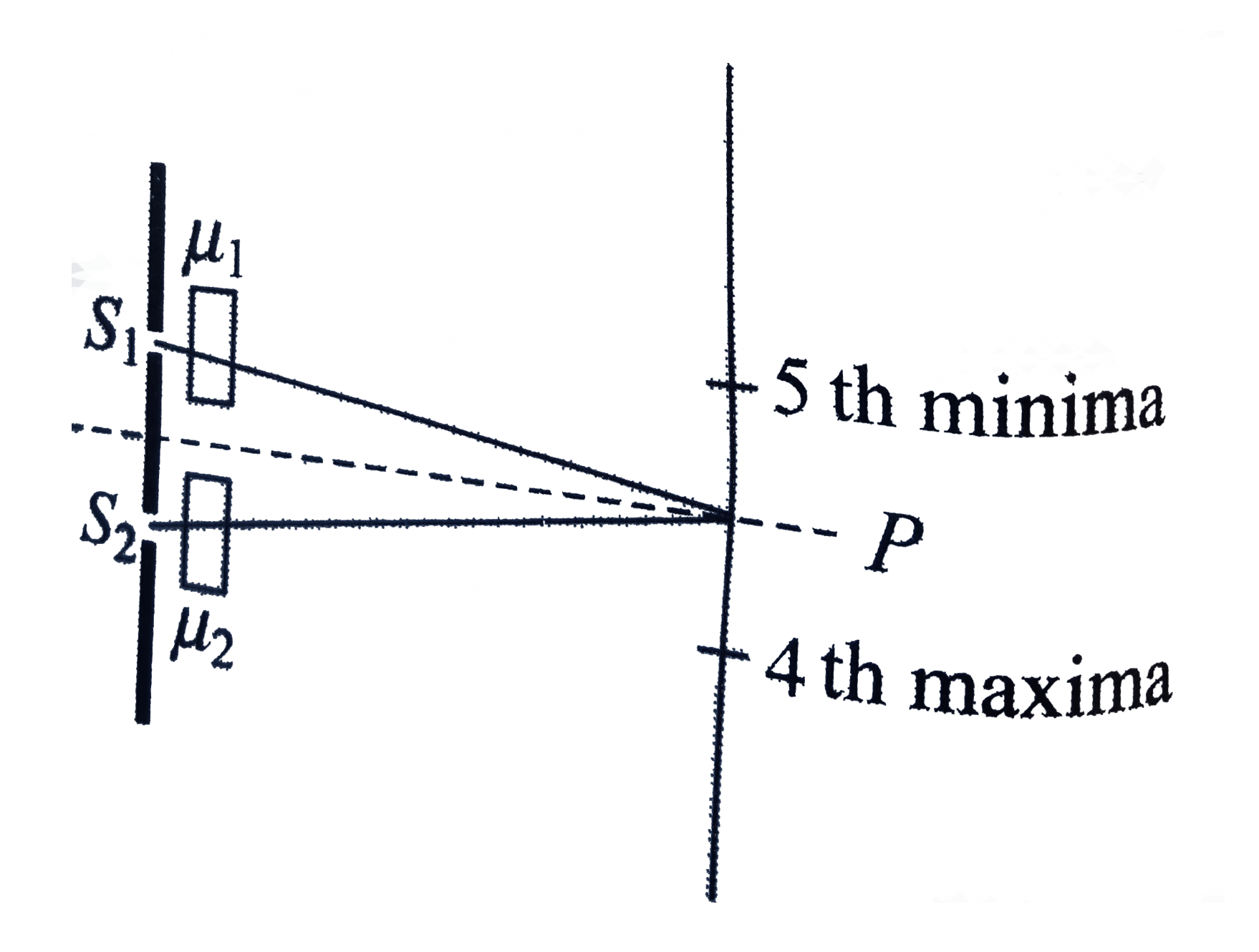
In young's experiment, the upper slit is covered by a thin glass plate of refractive index 43 and of thickness 9λ, where λ is the wavelength of light used in the experiment. The lower slit is also covered by another glass plate of thickness 2D & refractive index 32, as shown in figure. If I0 is the intensity at point P due to slits S1 & S2 each, then:

Intensity at point P is 4I0
Two fringes have been shifted in upward direction after inserted of both the glass plates together.
Optical path difference between te waves from S1 & S2 at point P is 2λ
If the source S is shifted upwards by a small distance d2 then the fringe originally at P after inserting the plates, shifts downwards by D(d2d1)
The correct Answer is:A, B, C, D
Optical path difference due to
S1 is =t(μ1−1)=9λ(43−1)=3λ
Optical path differ due to S2 is =t(μ2−1)=2λ(32−1)=λ
Path diff. at point PP=3λ−λ=2λ
Phase diff. 2πλ×2λ=4π
So net intensity at point P is
Inet=I0+I0+2I0cos4π
Inet=4I0
Optical path is consrved by S1 is more so fringe will shift at upper side.

Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
In a young 's double slit experiment, a glass plate of refractive index 1.5 and thickness 5×10−4 cm is kept in the path of one of the light rays. Then
View SolutionIn a Young.s double slit experiment, the fringes are displaced by a distance x when a glass plate of refractive index 1.5 is introduced in the path of one of the beams. When this plate is replaced by another plate of same thickness, the shift of fringes is (3/2)x. The refractive index of second plate is
View Solution
Knowledge Check
In a young 's double slit experiment, a glass plate of refractive index 1.5 and thickness 5×10−4 cm is kept in the path of one of the light rays. Then
AThere will be no shift in the interference patternBThe fringe width will increasesCThe fringe width will decreasesDThe optical path of the ray will increases by 2.5×10−4cmIn Young's double-slit experiment, if both the slits are covered by a thin transparent sheet of thickness t and refractive index n, the optical path difference between the two interfering waves
Aincreases by (n -1) tBdecrease by (n -1) tCchanges by Dd (n-1) tDis not affected.In Young's double slit experiment, the fringes are displaced by a distance x when a glass plate of one refractive index 1.5 is introduced in the path of one of the beams. When this plate in replaced by another plate of the same thickness, the shift of fringes is (3/2)x. The refractive index of the second plate is
A1.75B1.5C1.25D1
In Young’s experiment, the upper slit is covered by a thin glass plate of refractive index 1.4, while the lower slit is covered by another glass plate having the same thickness as the first one but having the refractive index 1.7. Interference pattern is observed using light of
wavelength 5400 Å . It is found that the point P on the screen where central maximum (n = 0) fall before the glass plate were inserted, now has % the original intensity. It is further observed that what used to be the fifth maximum earlier lies below the point P while the sixth minima lies above P. Calculate the thickness of glass plate. (Absorption of light by glass plate may be neglected).
View SolutionIn Young's experiment the upper slit is covered by a thin glass plate of refractive index 1.4 while the lower slit is covered by another glass plate, having the same thickness as the first one but having refractive index 1.7 interference pattern is observed using light of wavelength 5400Å
It is found that point P on the screen where the central maximum (n=0) fell before the glass plates were inserted now has 3/4 the original intensity. It is further observed that what used to be the fourth maximum earlier, lies below point P while the fifth minimum lies above P.
Calculate the thickness of glass plate. (Absorption of light by glass plate may be neglected.
 .
.
View SolutionIn Young's experiment the upper slit is covered by a thin glass plate of refractive index 1.4 while the lower slit is covered by another glass plate, having the same thickness as the first one but having refractive index 1.7 interference pattern is observed using light of wavelength 5400Å
It is found that point P on the screen where the central maximum (n=0) fell before the glass plates were inserted now has 3/4 the original intensity. It is further observed that what used to be the fourth maximum earlier, lies below point P while the fifth minimum lies above P.
Calculate the thickness of glass plate. (Absorption of light by glass plate may be neglected.
 .
.
View SolutionIn a Young's experiment, the upper slit is covered by a thin glass plate of refractive index 1.4 while the lower slit is covered by another glass plate having the same thickness as the first ont but having refractive index 1.7. Interference pattern is observed using light of wavelength 5400A. It is found that the point P on the screen where the central maximum fell berore the glass were inserted now has (3/4)th the original intensity. It is further observed that what used to be the 5th maximum earlier, Iies below the point O while the 6th minimum lies above O. The thickness of the glass plate in n×10−7m. Find the value of n
(Absorption of light by glass plate may by neglected)
View SolutionIn Young’s double slit experiment, the upper slit is covered by a thin glass plate of refractive index 1.4 while the lower slit is covered by another glass plate having same thickness as the first one but having refractive index 1.7.
Interference pattern is observed using light of wavelength5400∘A. It is found that the point P on the screen where the central maximum fell before the glass plates were inserted, now has 34 the original intensity. It is also observed that what used to be 5th maximum earlier, lies below the point P while the6th minimum lies above P. Calculate the thick- ness of glass plates. Absorption of light by glass plate may be neglected.
View Solution
