A particle of mass 1.5 kg moves along x-axis in a conservative force field. Its potential energy is given by V(x)=2x3−9x2+12x, where all quantities are written in SI units. The plot of this potential energy is given below.
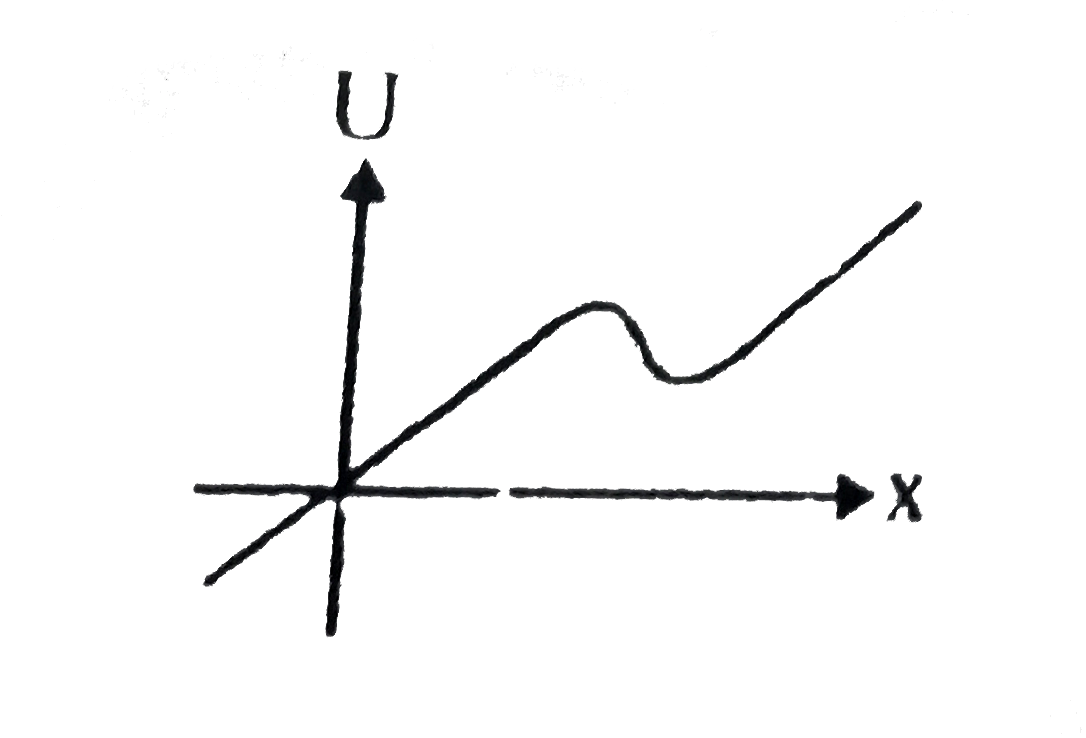 It is seen that the particle can be in stable equilibrium at a point on x-axis, x_(0). When it is displaced slightly from this equilibrium position, It executes SHM with time period T. What is the value of x0 ?
It is seen that the particle can be in stable equilibrium at a point on x-axis, x_(0). When it is displaced slightly from this equilibrium position, It executes SHM with time period T. What is the value of x0 ?
2m
3m
1m
1.5 m
The correct Answer is:A
Uminatx0=2m
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning75videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Multiple objective131videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic70videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE10videos
FLUID MECHANICS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
A particle of mass m is free to move along x axis under the influence of a conservative force. The potential energy of the particle is given by U=−axxe−bx [a and b are positive constants]
Find the frequency of small oscillations of the particle about its equilibrium positionView SolutionA partical of mass 2kg is moving on the x−axis with a constant mechanical energy 20J. Its potential energy at any x is U=(16−x2)J where x is in metre. The minimum velocity of particle is :−
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass 1.5 kg moves along x-axis in a conservative force field. Its potential energy is given by V(x)=2x3−9x2+12x, where all quantities are written in SI units. The plot of this potential energy is given below.
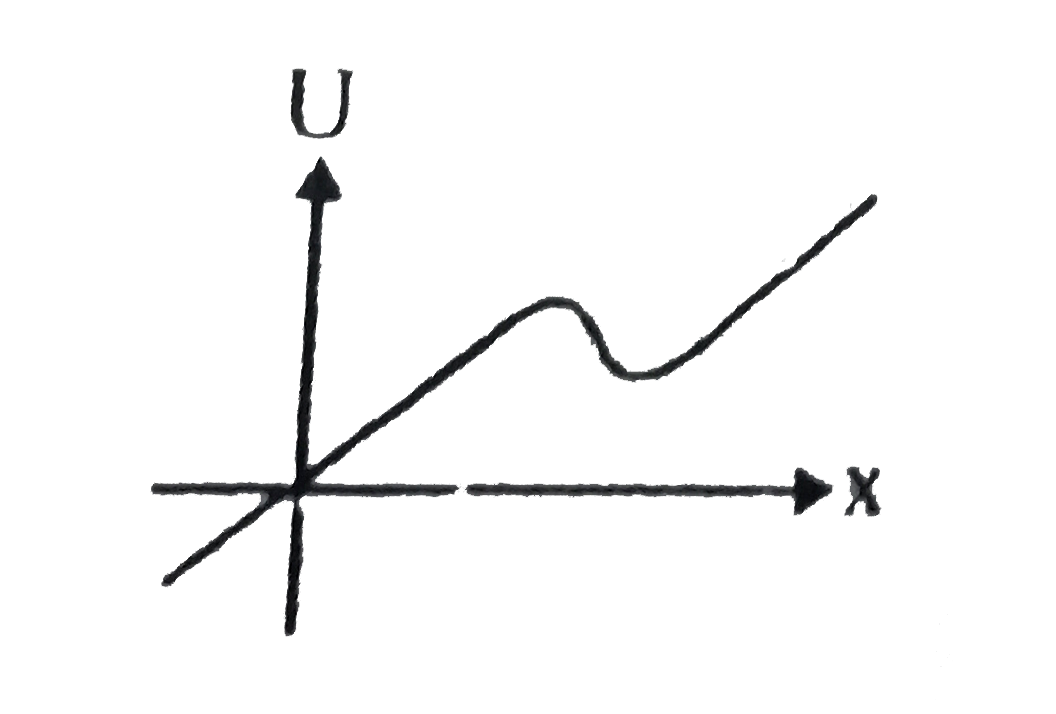 It is seen that the particle can be in stable equilibrium at a point on x-axis, x_(0). When it is displaced slightly from this equilibrium position, It executes SHM with time period T. What is the time period of SHM mentioned in the paragraph?AπsecB2πsecCπ2secDπ4sec
It is seen that the particle can be in stable equilibrium at a point on x-axis, x_(0). When it is displaced slightly from this equilibrium position, It executes SHM with time period T. What is the time period of SHM mentioned in the paragraph?AπsecB2πsecCπ2secDπ4sec - Question 2 - Select One
A particle of mass 1.5 kg moves along x-axis in a conservative force field. Its potential energy is given by V(x)=2x3−9x2+12x, where all quantities are written in SI units. The plot of this potential energy is given below.
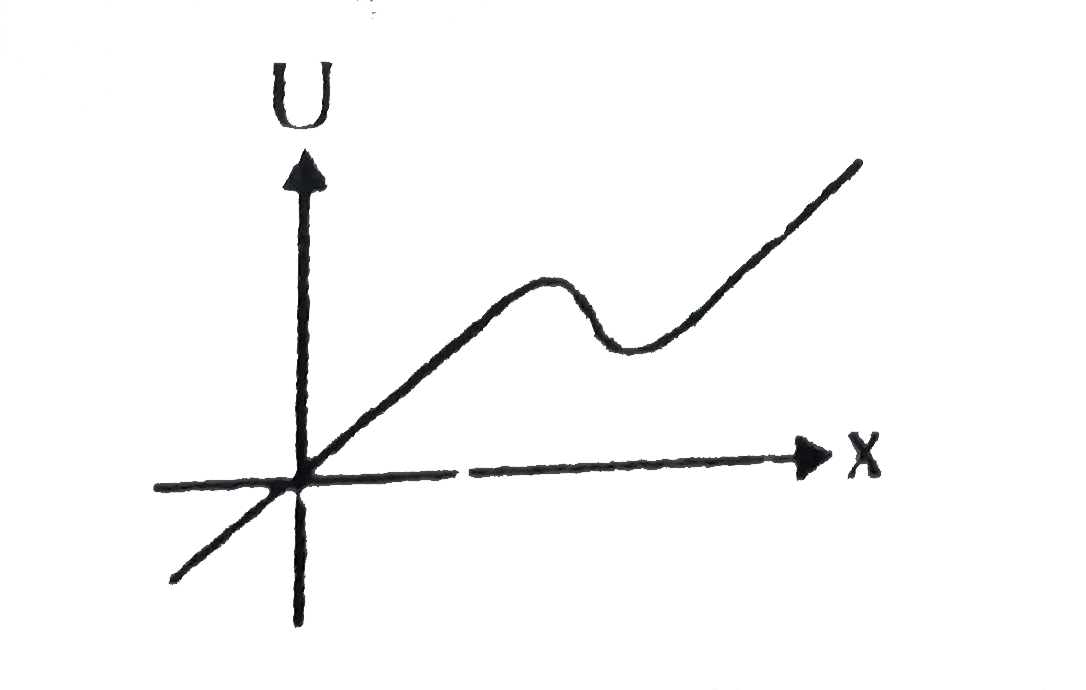 It is seen that the particle can be in stable equilibrium at a point on x-axis, x_(0). When it is displaced slightly from this equilibrium position, It executes SHM with time period T. What is the range of total mechanical energy of the particle for which its motion can be oscillatory about a pointAE<5JBE<8JCE<12JDE<9J
It is seen that the particle can be in stable equilibrium at a point on x-axis, x_(0). When it is displaced slightly from this equilibrium position, It executes SHM with time period T. What is the range of total mechanical energy of the particle for which its motion can be oscillatory about a pointAE<5JBE<8JCE<12JDE<9J - Question 3 - Select One
A particle of mass m is executing osciallations about the origin on the x-axis with amplitude A. its potential energy is given as U(x)=αx4, where α is a positive constant. The x-coordinate of mass where potential energy is one-third the kinetic energy of particle is
A±A2B±A√2C±A3D±A√3
A particle of mass m is located in a one dimensional potential field where potential energy of the particle has the form U(x)=ax2−bx where a and b are positive constants. The position of equilibrium is:
View SolutionA particle of mass 2 kg moving along x-axis has potential energy given by, U=16x2−32x ( in joule), where x is in metre. Its speed when passing through x=1is2ms−1
View SolutionA particle of mass m is executing oscillations about origin on the x axis amplitude A its potential energy is given asU(x)=βx4 where β is constant x cooridirate of the particle where the potential energy is one third of the kinetic energy is
View SolutionPotential energy of a particle is related to x coordinate by equation x2−2x . Particle will be in stable equilibrium at :
View SolutionSpeed v of a particle moving along a straight line, when it is a distance X from a fixed point on the line is given by V2=108−9X2 (all quantities in S.I. unit). Then
View Solution

