A small particle of mass m is attached at B to a hoop of mass m and radius r, whole system is placed on the rough horizontal ground. The system is released from rest when B is dierctly above A and rolls without slipping. Find the angular acceleration of the system at the instant when AB becomes horizontal as shown in the figure.
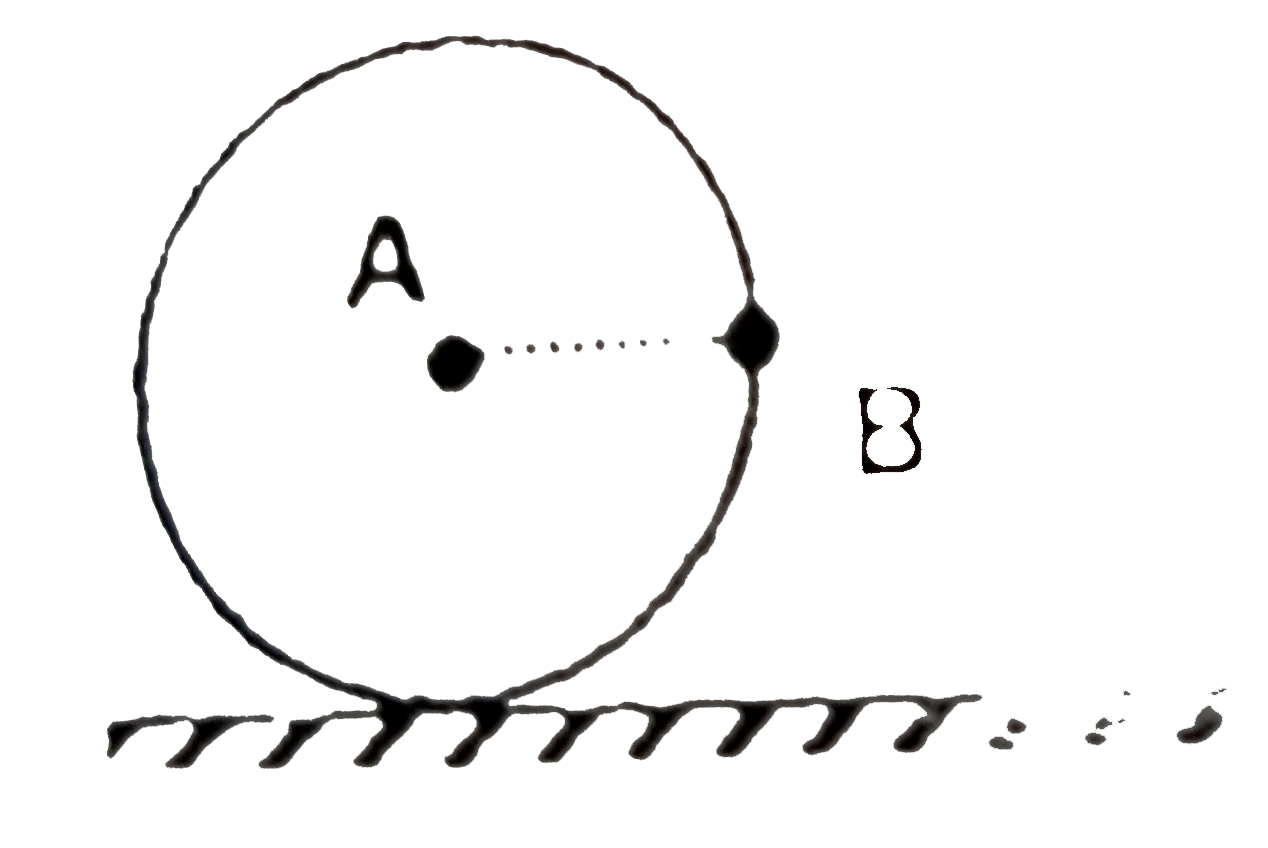
Assuming that the hoop rotates by θ (so that the attached particle also rotates by θ) starting from its initial position, we find the angular speed of the hoop + particle.
The instantaneous axis of rotation is located at P. we apply conservation of mechanical energy to get
mgR(1−cosθ)=12(2mR2)ω2+12m(2Rcosθ2ω)2
Differentiating and putting θ=90∘
We solve for α=ωdωdθ and get 4α=3g2R
or α=3g8R

Topper's Solved these Questions
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Objective problems
215 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Assertion & Reason
15 Videos
- GENERAL PHYSICSBOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE
3 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question
2 Videos
Similar Questions
A particle of mass m is rigidly attached at A to a ring of mass 3m and radius r. The system is released from rest and rolls without sliding. The angular acceleration of ring just after release is

View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View Solution
Knowledge Check
A particle of mass 'm' is rigidly attached at 'A' to a ring of mass 3m and radius 'r' . The system is released from rest and rolls without sliding. The angular release is acceleration of ring just after release after
 Ag4rBg6rCg8rDg2r
Ag4rBg6rCg8rDg2rA uniform disc of mass M and radius R is supported vertically by a pivot at its periphery as shown. A particle of mass M is fixed to the rim and raised to the highest point above the center. The system is released from rest and it can rotate about pivot freely. The angular speed of the system when the attached object is directly beneath the pivot, is
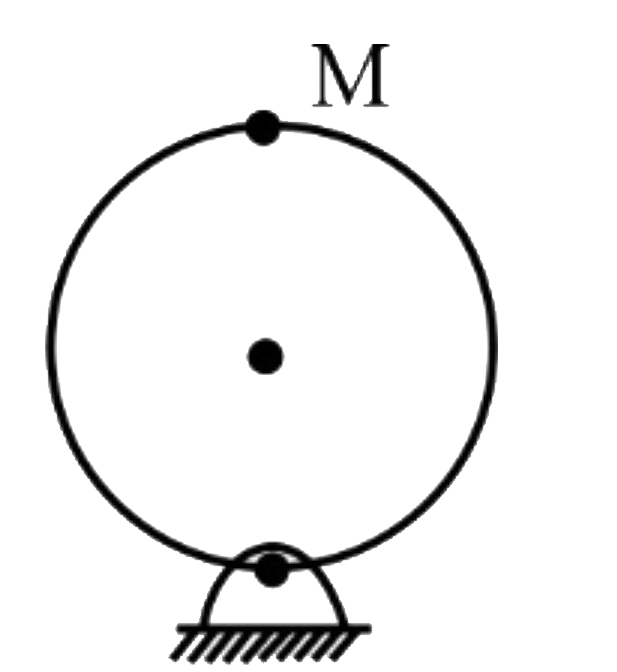 A√24g11RB√8g11RC√8g3RD√14g3R
A√24g11RB√8g11RC√8g3RD√14g3R
A block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA semicircle disc of mass M and radius R is held on a rough horizontal surface as shown in figure. The centre of mass C of the disc is at a distance of 4R3π from the point O. Now the disc is released from this position so that it starts rolling without slipping. Find
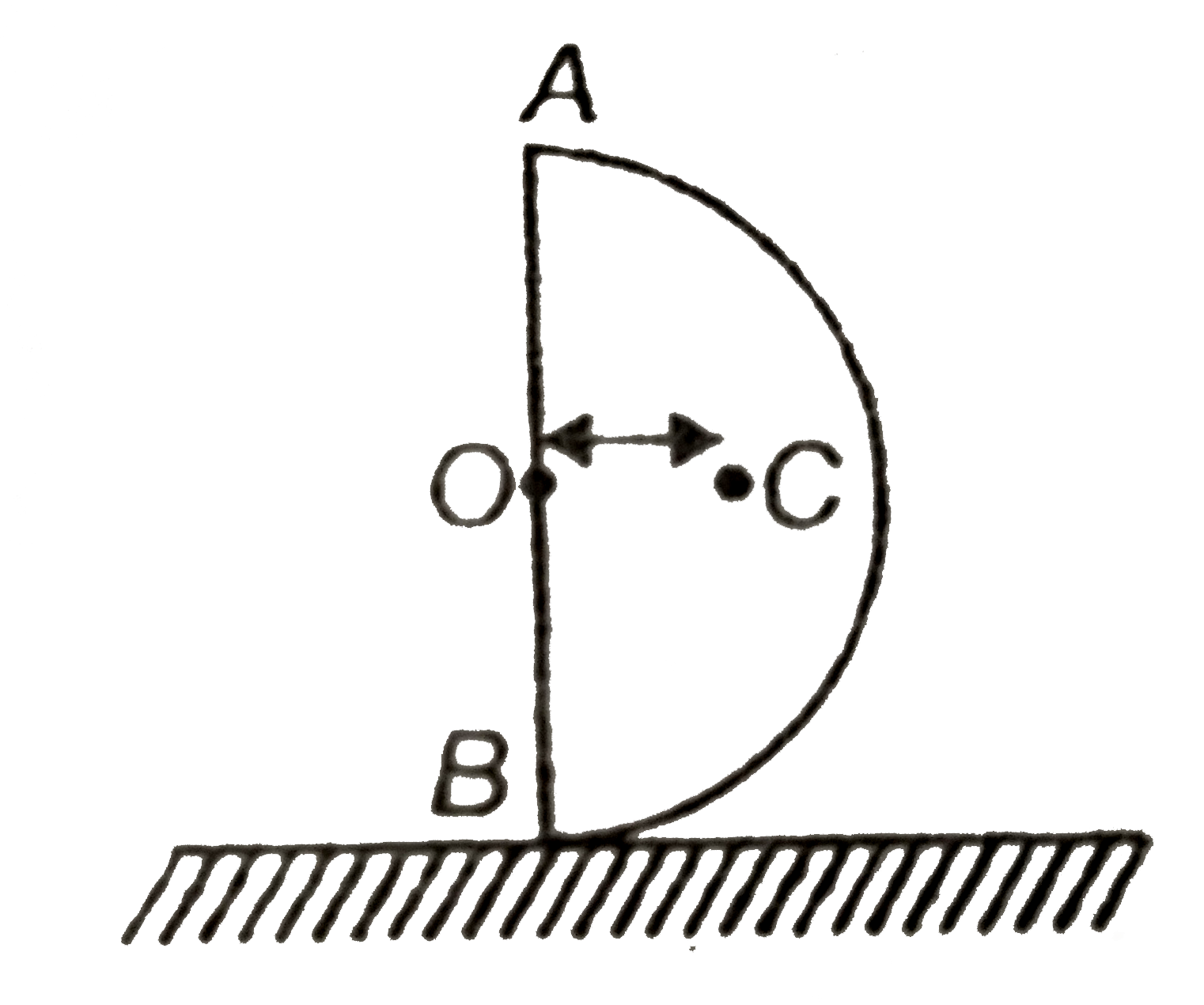
(a) The angular acceleration of the disc at the moment it is relased from the given position.
(b) The minimum co-efficient of fricition between the disc and ground so that it can roll without slipping.
View SolutionA semicircle disc of mass M and radius R is held on a rough horizontal surface as shown in figure. The centre of mass C of the disc is at a distance of 4R3π from the point O. Now the disc is released from this position so that it starts rolling without slipping. Find

(a) The angular acceleration of the disc at the moment it is relased from the given position.
(b) The minimum co-efficient of fricition between the disc and ground so that it can roll without slipping.
View SolutionA uniform disc of mass M and radius R is supported vertically by a pivot at its periphery as shown. A particle of mass M is fixed to the rim and raised to the highest point above the center. The system is released from rest and it can rotate about pivot freely. The angular speed of the system when the attached object is directly beneath the pivot, is

View Solution
