In the figure shown when the massless spring is in released state its free end is at point B. A very small block is ressed against the spring by a distance δ and the released from rest. Except the portion BC where coefficient of kinetic friction is μk, track is smooth everywhere. Determine the spring compression δ so that the block enters a small hole at E. Consider all values shown in the figure.
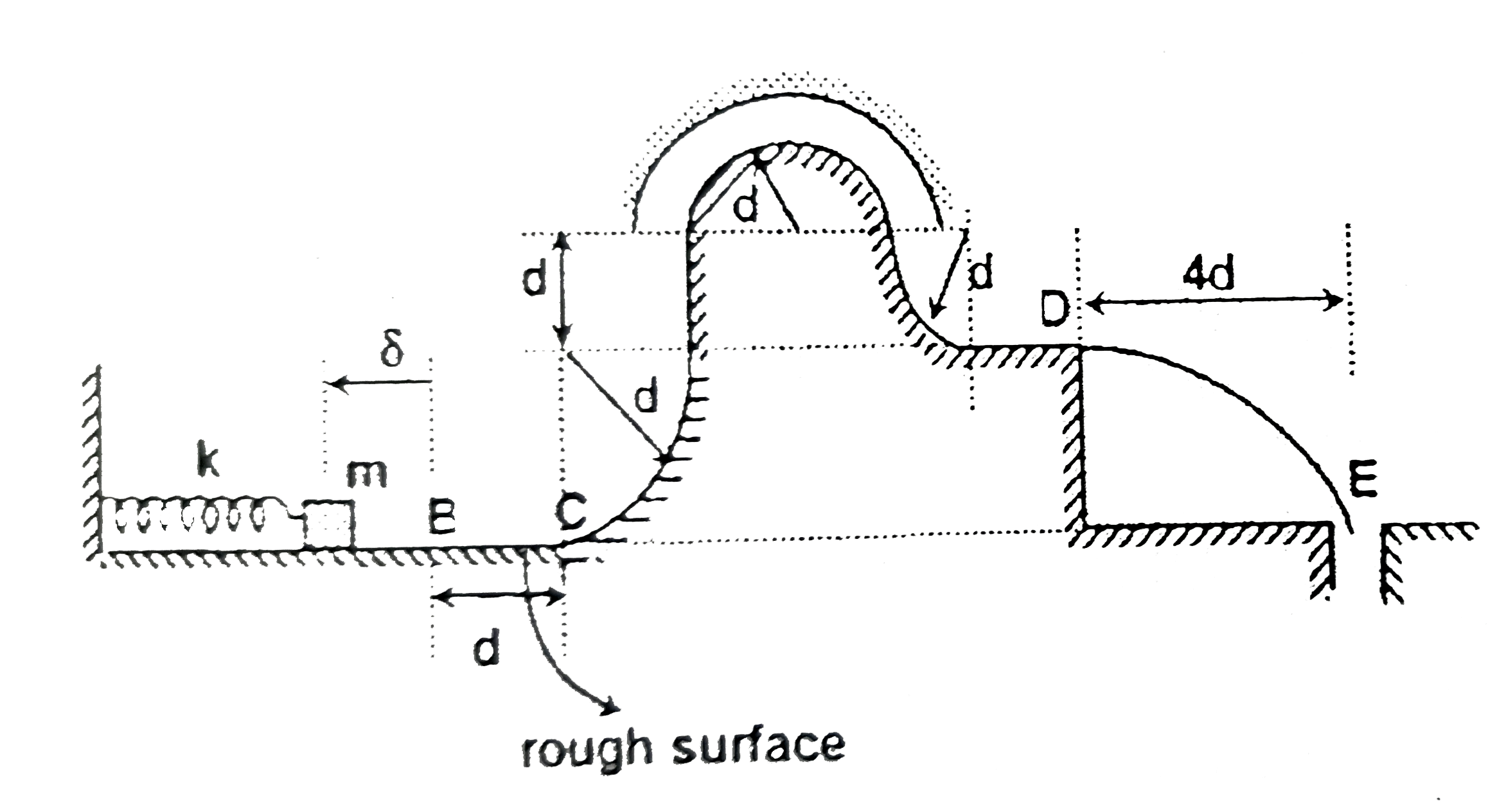
We determine the speed required at D so that the block falls into the hole at E by following a parbolic trajectory.
vd=speed at D
vd=√8gd
Applying conservation of energy for motion from A to D
12kδ2=μkmgd+mgd+12m(8gd)⇒δ=√2mgdk(μK+5)
Topper's Solved these Questions
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Objective problems
215 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Assertion & Reason
15 Videos
- GENERAL PHYSICSBOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE
3 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question
2 Videos
Similar Questions
In the figure shown when the massless spring is in relaxed state, its free end is at point B. A very small block is pressed against the spring by a distance δ and then released from rest. Except the portion BC where coefficient of kinetic is μ, track is smooth everywhere. Determine the spring compression δ so that the block enters a small hole at E. Consider all value shown in the figure.If δ is given by δ=x[mgd(5+μ)2K]12, find x. Block never leaves contact with surface
View SolutionThe spring is compressed by a distance a and released. The block again comes to rest when the spring is elongated by a distance b. During this
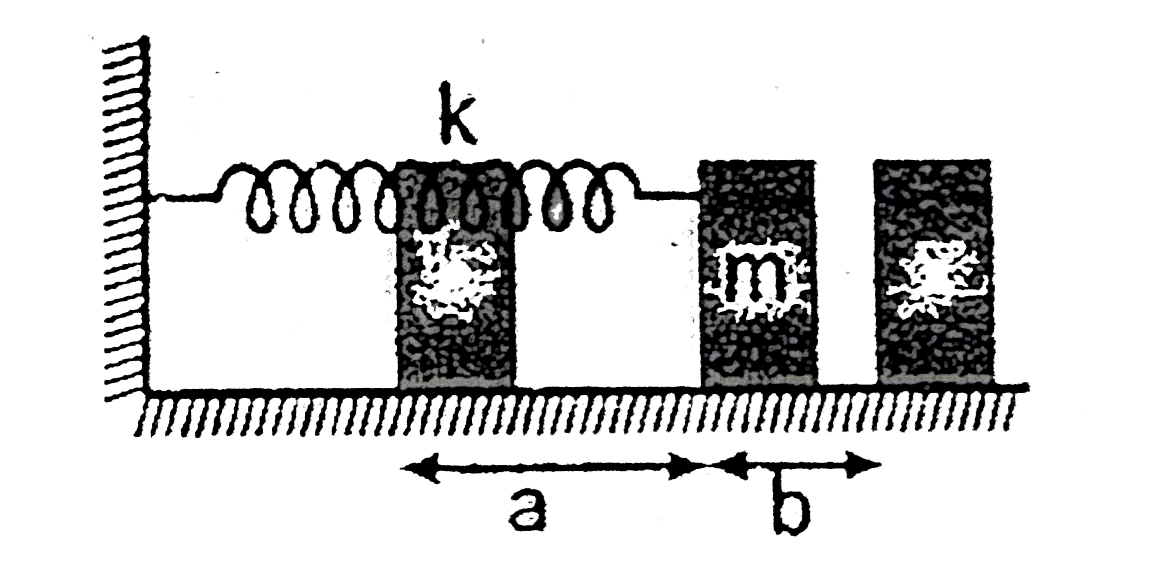
View Solution
Knowledge Check
The spring is compressed by a distance a and released. The block again comes to rest when the spring is elongated by a distance b. During this
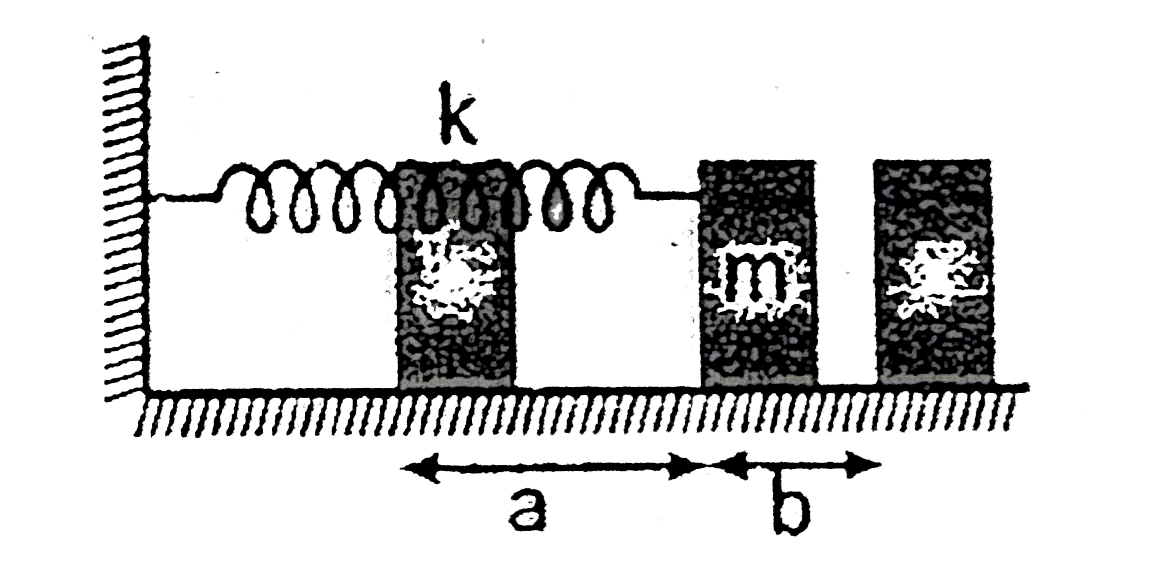 Awork done by sprinn on the block =12k(a+b)2Bwork done by sprinn on the block =12k(a2−b2)Cco-eff. of frication =k(a−b)2mgDco-eff. of frication =k(a+b)2mg
Awork done by sprinn on the block =12k(a+b)2Bwork done by sprinn on the block =12k(a2−b2)Cco-eff. of frication =k(a−b)2mgDco-eff. of frication =k(a+b)2mgA block with mass 0.50kg is forced against a horizontal spring of negligible mass , compressing the spring a distance of 0.20m (figure). When released, the block moves on a horizontal table top for 1.00N/m. What is the coefficient of kinetic friction μk, between the block and the block and the table?
 A0.40B0.50C0.25Dnone of these
A0.40B0.50C0.25Dnone of theseIn the figure shown a block of masss m is atteched at ends of two spring The other ends of the spring are fixed The mass m is released in the vertical plane when the spring are released The velocity of the block is maximum when
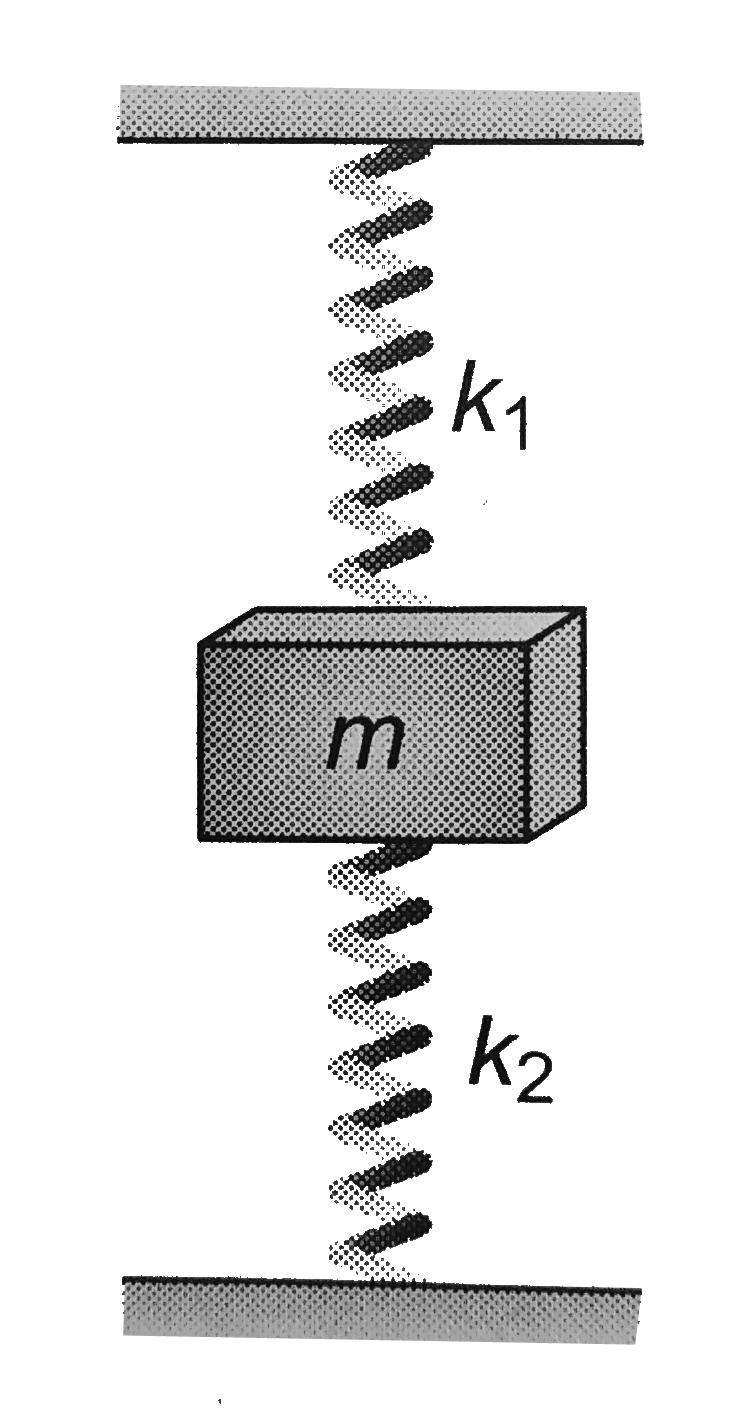 Ak1 is compressed and k2 is elongatedBk1 is elongated and k2 is compressedCk1 and k2 both are compressedDk1 and k2 both are elongated.
Ak1 is compressed and k2 is elongatedBk1 is elongated and k2 is compressedCk1 and k2 both are compressedDk1 and k2 both are elongated.
A block of mass m is pressed against a spring of force constant k. The block after leaving contact with the spring moves along a ''loop'' the loop track. The sliding surface is smooth except for rough portion of length s equal to R as shown in Fig. 3E.34, where the coefficient of friction is μk. Determine the minimum spring compression x for which the particle will not lose contant with the track ?

View SolutionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.

View SolutionThe block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m

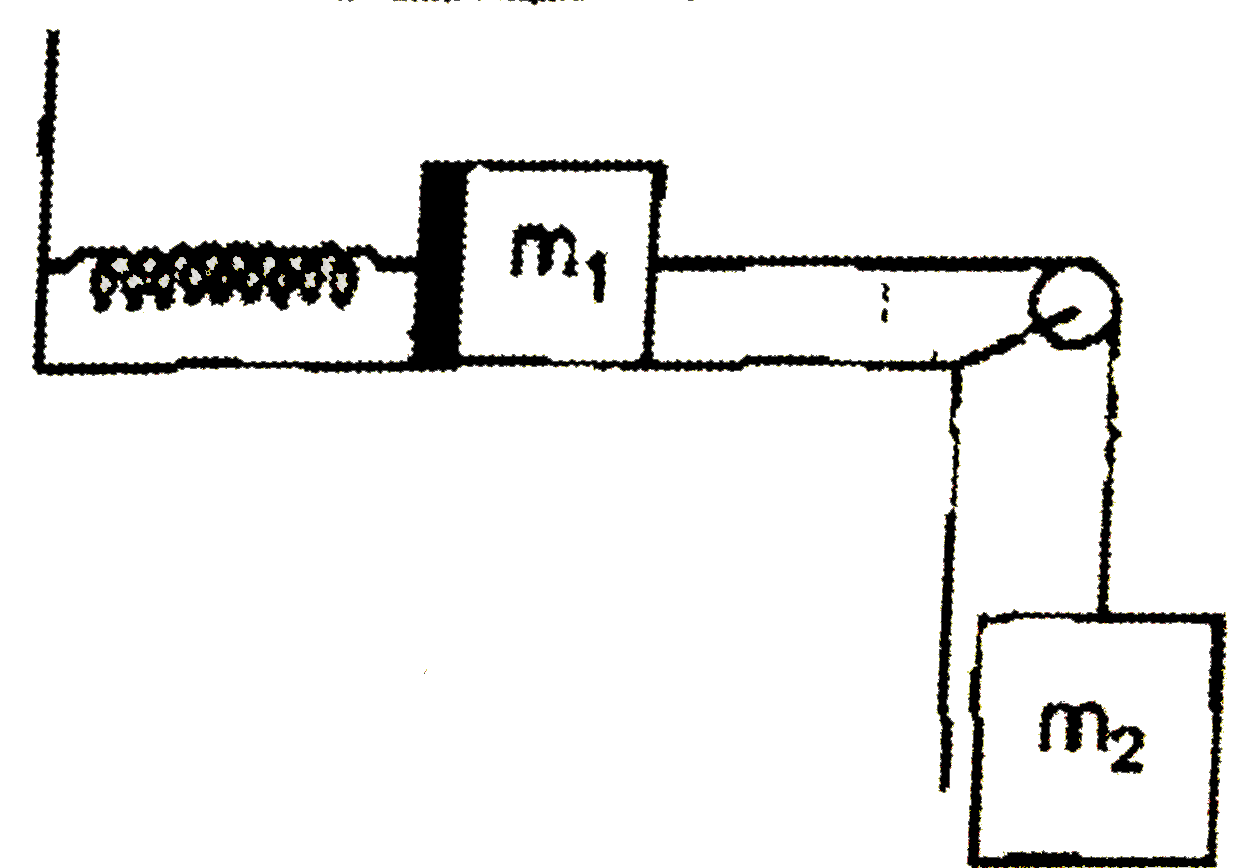
View SolutionIn Fig 3E.17, the mass m2 rests on a rough table. The mass m1 is pushed against the spring to which it is not attached Force constant of the spring is k, coefficient of friction is μk.
(a) Find the speed of the blocks after the spring is released and m2 has fallen a distance of h.
(b) If the spring is attached to the block and it falls a distance h before coming to rest, calculate the coefficient of friction μk.
View SolutionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.

View Solution
