The figure shows a snap photograph of a vibrating string at t=0. The particle P is observed moving up with velocity 20√3cm/s. The tangent at P makes an angle 60∘ with x-axis.
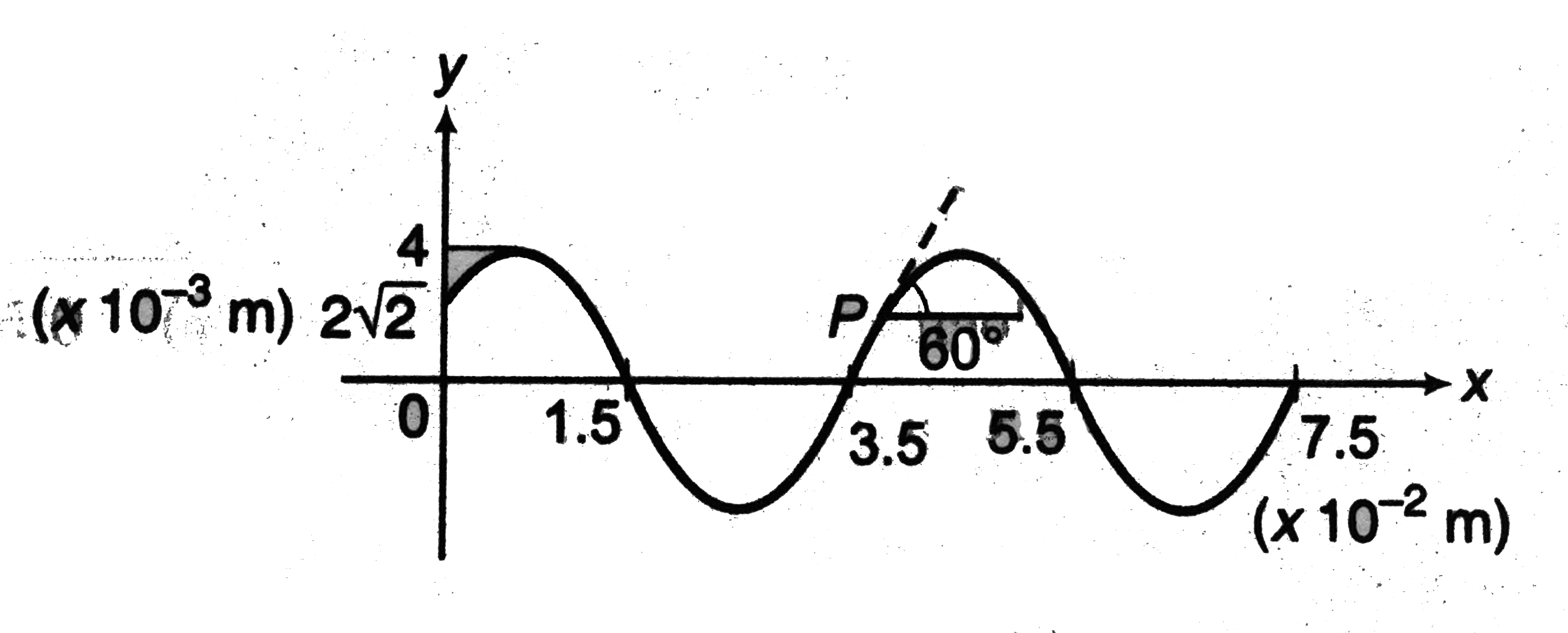
(a) Find the direction in which the wave is moving.
(b) Write the equation of the wave.
(c) The total energy carries by the wave per cycle of the string. Assuming that the mass per unit length of the string is 50g/m.
(a) P is moving up i.e. has positive velocity, particle velocity,
vp=−v(dydx)……(1) v=wave velocity
dydx= slope at point P=tan60∘=√3
As vP and dydx are both positive hence v must be negative, hence the wave is moving in negative x-axis.
(b) The equation of the wave
y=asin(ωt−kx+δ)......(2)
ω=2πn and k=ωv=2πλ=π2cm−1
a=4×10−3m=0.4cm At t=0, x=0 and y=2×10−3m=0.2cm
Substituting in (2)
2√2×10−3=4×10−3sinδ, which gives δ=π4 or 3π4
Also at t=0, x=1.5cm. And y=0
0=asin(0−3π4+δ) which gives δ=3π4
hence, δ=3π4
20√3=−v×tan60∘ ,
v=−20cm/s(-sign because wave is moving in negative direction)
Hence, n=v/λ=5Hz.
Hence, ω=2π×5=10π
Substituting the values of a, ω, k and δ
We get,
y=0.4sin(10πt−π2x+π6)
or y=0.4sin2π(5t−x4+112).
Topper's Solved these Questions
Similar Questions
A carpet of unit mass an unit length is laid on the floor. One end of the carpet is bent back and then pulled backwards with constants. Unit velocity, just above the part of the carpet which is still at rest on the floor. Find the speed of the centre of mass of the moving part. What is the minimum force needed to pull the moving part ?
 06:45View Solution
06:45View SolutionA horizontally oriented bent thin tube ABC of length 1.4m rotates with a constant angular velocity ω about a stationary vertical axis OO' passing through the end A as shown in figure. The portion BC of tube is parallel to OO' and its length is equal 0.4m. At t=0, AB part of tube is filled with an ideal fluid. The end A of tube is open, the closed end C has a very small orifice. Find the maximum height reached by fluid relative to end C. (take g=10/s2 and ω=10rad/s)
 06:31View Solution
06:31View SolutionThe figure shows a snap photograph of a vibrating string at t = 0 . The particle P is observed moving up with velocity 20sqrt(3) cm//s . The tangent at P makes an angle 60^(@) with x-axis. (a) Find the direction in which the wave is moving. (b) Write the equation of the wave. (c) The total energy carries by the wave per cycle of the string. Assuming that the mass per unit length of the string is 50g//m .
03:06View SolutionThe figure represents two snaps of a travelling wave on a string of mass per unit length mu=0.25 kg//m . The first snap is taken at t=0 and the second is taken at t=0.05 s . Determine the equation of the wave.
03:40View Solutionएक डोरी में X-दिशा में गतिमान तरंग का समीकरण y=3sin[314t−3.14x] है, जहाँ y तथा x सेमी में एवं t सेकण्ड में है । ज्ञात कीजिये -
(i) डोरी में तरंग की चाल, (ii) तरंग की आवृत्ति, (iii) तरंग की तरंग-दैर्ध्य (iv) डोरी के किसी कण की अधिकतम चाल ।03:42View Solutionएक डोरी पर चलती तरंग का समीकरण है ,
y=(0.10mm)sin[(31.4m−1x+(314s−1)t].
(a) तरंग किस दिशा में चल रही है ? (b) तरंग की चाल , तरंगदैर्ध्य तथा आवृत्ति निकालें । (c )डोरी के किसी कण का अधिकतम विस्थापन तथा उसकी अधिकतम चाल निकालें ।04:10View SolutionA transverse sinusoidal wave moves along a string in the positive x-direction at a speed of 10 cm/s. The wavelength of the wave is 0.5 m and its ampli- tude is 10 cm. At a particular time t, the snap-shot of the wave is shown in figure. The velocity of point P when its displacement is 5 cm is Figure :
 03:20View Solution
03:20View SolutionA transvers sinusoidal wave move along a string in the positive x-direction at a speed of 10 cm/s. The wavelength of the wave is 0.5 m and its amplitude is 10 cm . At a particular time t, the snap-shot of the wave is shown in figure . The velocity of point P when its displacement is 5 cm is :
View SolutionThe amplitude of a wave produced in a string is 5 cm. The wave is moving along positive direction of X-axis with a speed of 150 m/s and 5 vibrations are completed in 3 m length of the string. The equation representing the wave will be
View SolutionSnapshot of a string carrying a progressive wave is shown in figure at time t = 0. The wave moves along positive x - axis:
 04:41View Solution
04:41View SolutionThe figure shows a snap photogaraph of a vibrating siring ai l = 0. The particle P is observed moving up with velocity 20sqrt(3) cm/s. The tangent at P makes an aggie 60IJ with x-axis. The mass per unit length of string is 50 g/m:
08:45View SolutionThe figure shows a snap photograph of a vibrating string at t = 0. The particle P is observed moving up with velocity 20√3 cm/s. The tangent at P makes an angle 60∘ with x-axis.
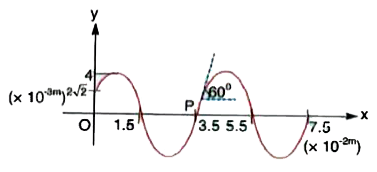
Find the direction in which the wave is moving.View SolutionThe figure shows a snap photograph of a vibrating string at t = 0. The particle P is observed moving up with velocity 20 sqrt3 cm/s. The tangent at P makes an angle 60^@ with x-axis. Write the equation of the wave.
06:07View SolutionThe figure shows a snap photograph of a vibrating string at t = 0. The particle P is observed moving up with velocity 20 sqrt3 cm/s. The tangent at P makes an angle 60^@ with x-axis. Find the total energy carried by the wave per cycle of the string. Assume that the mass per unit length of the string = 50 g/m.
02:05View SolutionThe figure shows a snap photograph of a vibrating string at t=0. The particle P is observed moving up with velocity 20√3cm/s. The tangent at P makes an angle 60∘ with x-axis.

(a) Find the direction in which the wave is moving.
(b) Write the equation of the wave.
(c) The total energy carries by the wave per cycle of the string. Assuming that the mass per unit length of the string is 50g/m.05:05View SolutionThe figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
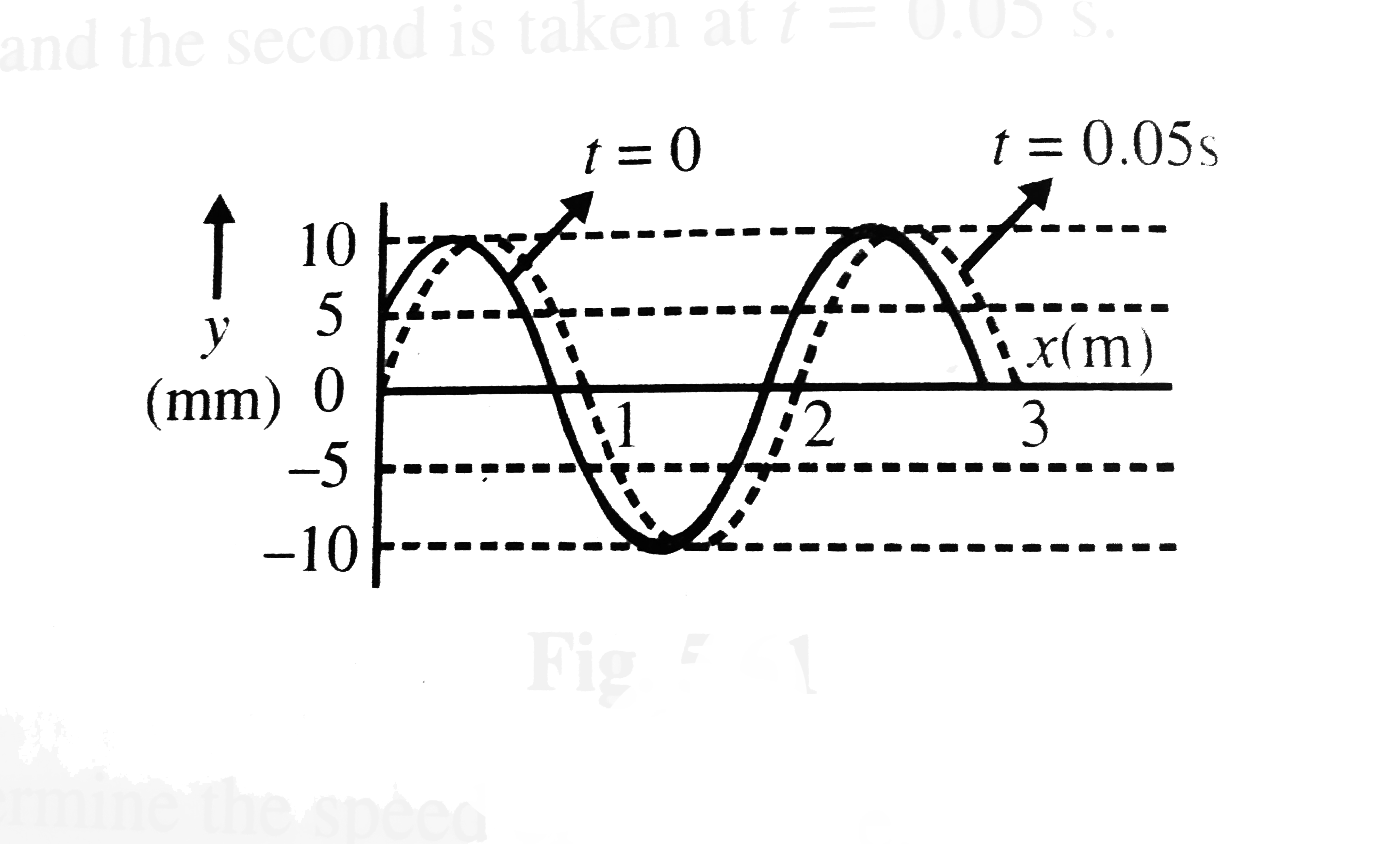
Determine the equation of the wave.04:12View Solution

