The figure shows a snap photogaraph of a vibrating siring ai l = 0. The particle P is observed moving up with velocity 20√3 cm/s. The tangent at P makes an aggie 60IJ with x-axis. The mass per unit length of string is 50 g/m:
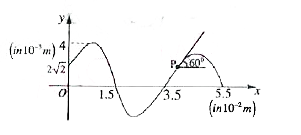
wave is moving along positive x-direction
The equation of the wave is y=0.4sin(10πt−π2x)
Total energy carried by the wave per cycle of the striiig is 1.6×10−5 J
The equation of the wave is y=4mmsin(10πt+π2x+π4)
The correct Answer is:A, B, C, D
Similar Questions
The figure shows a snap photograph of a vibrating string at t=0. The particle P is observed moving up with velocity 20√3cm/s. The tangent at P makes an angle 60∘ with x-axis.
(a) Find the direction in which the wave is moving.
(b) Write the equation of the wave.
(c) The total energy carries by the wave per cycle of the string. Assuming that the mass per unit length of the string is 50g/m.
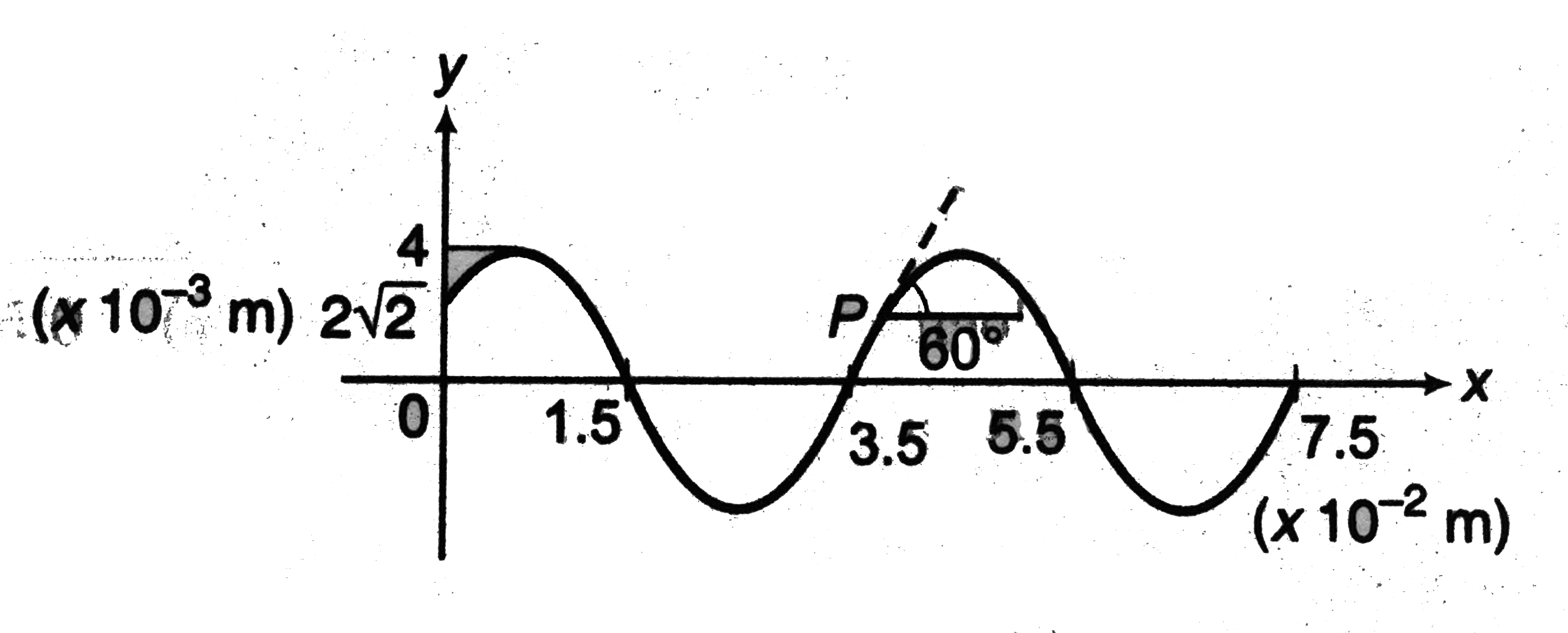
View SolutionThe figure shows a snap photograph of a vibrating string at t=0. The particle P is observed moving up with velocity 20√3cm/s. The tangent at P makes an angle 60∘ with x-axis.

(a) Find the direction in which the wave is moving.
(b) Write the equation of the wave.
(c) The total energy carries by the wave per cycle of the string. Assuming that the mass per unit length of the string is 50g/m.
View Solution
Knowledge Check
Figure shows the graph of velocity versus time for a particle going along x axis. Initially at t = 0, particle is at x = 3m. Find position of particle at t = 2s. (in m)
 A9mB3mC12mD6m
A9mB3mC12mD6m
The figure shows a snap photograph of a vibrating string at t=0. The particle P is observed moving up with velocity 20√3cm/s. The tangent at P makes an angle 60∘ with x-axis.

(a) Find the direction in which the wave is moving.
(b) Write the equation of the wave.
(c) The total energy carries by the wave per cycle of the string. Assuming that the mass per unit length of the string is 50g/m.
View SolutionA light thread is tightly wrapped around a fixed disc of radius R. A particle of mass m is tied to the end P of the thread and the vertically hanging part of the string has length πR. The particle is imparted a horizontal velocity V=√4πgR3. The string wraps around the disc as the particle moves up. At the instant the velocity of the particle makes an angle of θ=60∘ with horizontal, calculate.
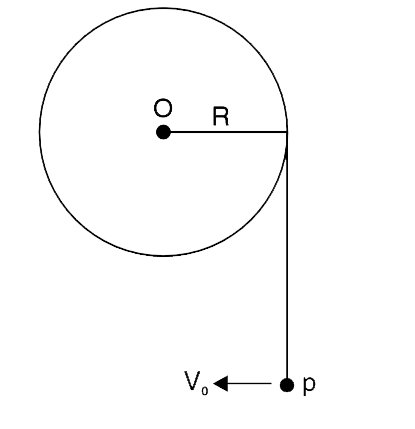
(a) Speed of the particle
(b) Tension in the string
View SolutionA particle having charge q=+2.00μC and mess m=0.0100kg is connected to a string having length L=1.50 m and is tied to the pivot point P shown in the figure. The particle, string, and pivot point all lie op a frictionless horizontal table. The particle is released from rest when the string makes an angle θ=60∘ with a uniform electric field of magnitude E=300 V / m .The speed (in m / s ) of the particle when the string is parallel to the electric field (shown in figure) is x. Find 10x.
'(##CEN_KSR_PHY_JEE_C18_E01_021_Q09##)'
View SolutionThe velocity of transverse wave in a string is v=√T/m where T is the tension in the string and m is the mass per unit length . If T=3.0kgf, the mass of string is 25g and length of the string isv=1.000m, then the percentage error in the measurement of velocity is
View SolutionThe acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.

View SolutionThe acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.

View SolutionA big particle of mass (3+m) kg blasts into 3 pieces , such that a particle of mass 1 kg moves along x - axis , with velocity 2ms−1 and a particle of mass 2 kg moves with velocity 1ms−1 perpendicular to direction of 1 kg particle . If the third particle moves with velocity √2ms−1, then m is
View Solution
