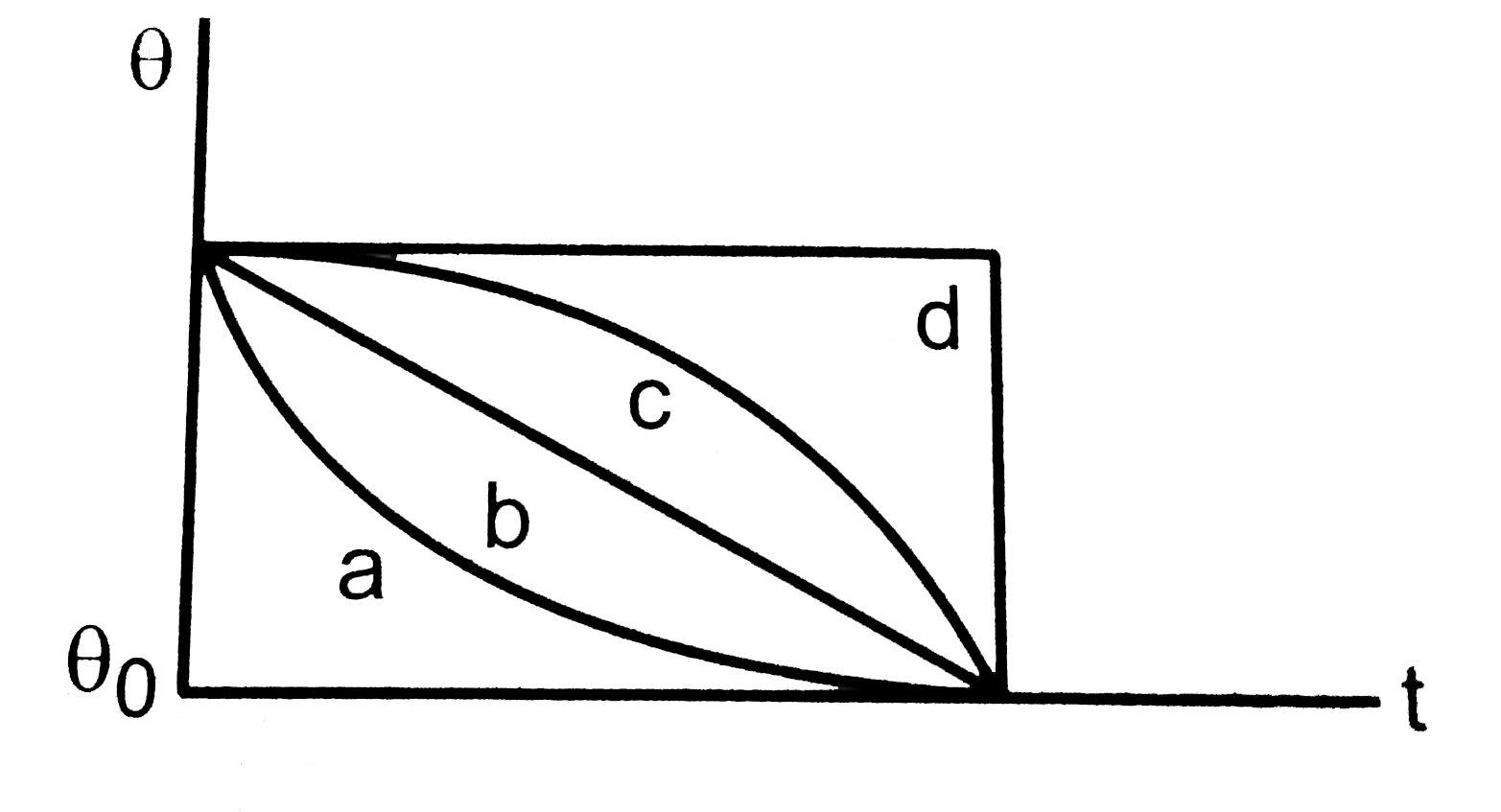
A block of metal is heated to a temperature much higher than the room temperature and allowed to cool in a room free from air currents. Which of the following curves correctly represents the rate of cooling
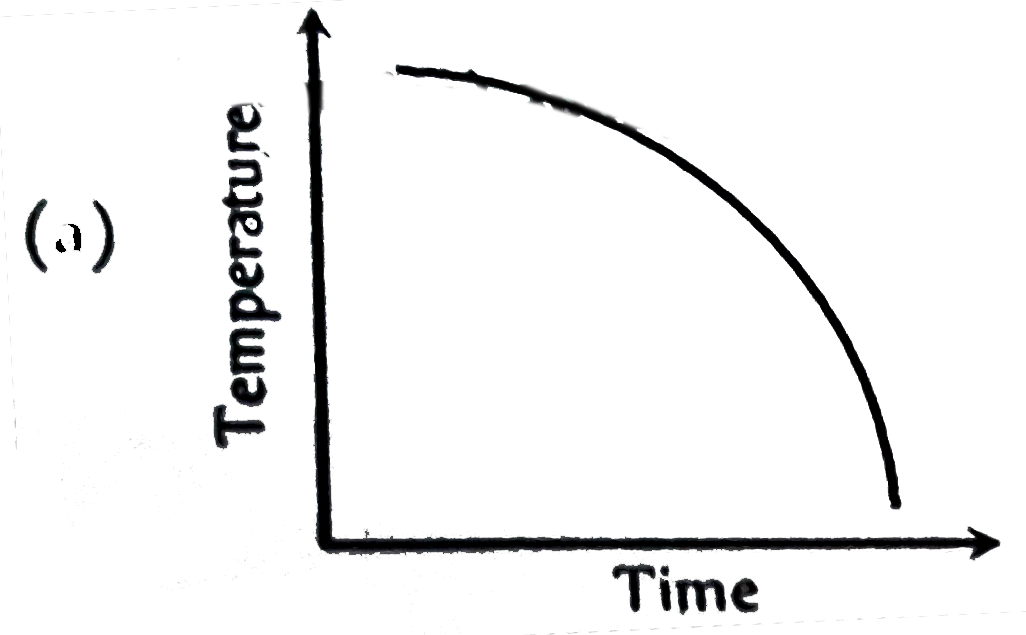


The correct Answer is:B
To solve the problem of determining which curve correctly represents the rate of cooling of a heated metal block in a room free from air currents, we can follow these steps:
1. Understand the Scenario:
- A block of metal is heated to a temperature much higher than the room temperature and is allowed to cool in a still environment (no air currents).
2. Apply Newton's Law of Cooling:
- According to Newton's Law of Cooling, the rate of cooling of an object is directly proportional to the temperature difference between the object and its surroundings.
- Mathematically, this can be expressed as:
dθdt=−k(θ−θ0)
where:
- θ = temperature of the object at time t
- θ0 = ambient (room) temperature
- k = positive constant of proportionality
3. Rearranging the Equation:
- Rearranging gives:
dθ=−k(θ−θ0)dt
4. Integrate the Equation:
- Integrating both sides, we get:
∫1θ−θ0dθ=−k∫dt
- This results in:
ln|θ−θ0|=−kt+C
- Exponentiating both sides gives:
θ−θ0=Ce−kt
- Where C is a constant determined by initial conditions.
5. Final Temperature Equation:
- Rearranging gives:
θ(t)=θ0+Ce−kt
- This shows that the temperature of the block decreases exponentially over time.
6. Identify the Correct Graph:
- The graph of θ(t) as a function of time t will show an exponential decay, starting from the initial temperature and approaching the ambient temperature θ0 asymptotically.
- Among the provided options, we need to identify which curve represents this exponential decay.
Conclusion:
- The correct curve representing the rate of cooling of the metal block will be the one that shows an exponential decrease in temperature over time.
- A block of metal is heated to a temperature much higher than the room temperature and is allowed to cool in a still environment (no air currents).
- According to Newton's Law of Cooling, the rate of cooling of an object is directly proportional to the temperature difference between the object and its surroundings.
- Mathematically, this can be expressed as:
dθdt=−k(θ−θ0)
where:
- θ = temperature of the object at time t
- θ0 = ambient (room) temperature
- k = positive constant of proportionality
- Rearranging gives:
dθ=−k(θ−θ0)dt
- Integrating both sides, we get:
∫1θ−θ0dθ=−k∫dt
- This results in:
ln|θ−θ0|=−kt+C
- Exponentiating both sides gives:
θ−θ0=Ce−kt
- Where C is a constant determined by initial conditions.
- Rearranging gives:
θ(t)=θ0+Ce−kt
- This shows that the temperature of the block decreases exponentially over time.
- The graph of θ(t) as a function of time t will show an exponential decay, starting from the initial temperature and approaching the ambient temperature θ0 asymptotically.
- Among the provided options, we need to identify which curve represents this exponential decay.
- The correct curve representing the rate of cooling of the metal block will be the one that shows an exponential decrease in temperature over time.
Topper's Solved these Questions
- TRANSMISSION OF HEATBOOK - ERRORLESS CHAPTER - TRANSMISSION OF HEATEXERCISE - Assertion & Reason
24 Videos
- TRANSMISSION OF HEATBOOK - ERRORLESS CHAPTER - TRANSMISSION OF HEATEXERCISE - ET Self Evaluation Test
23 Videos
- TRANSMISSION OF HEATBOOK - ERRORLESS CHAPTER - TRANSMISSION OF HEATEXERCISE - Critical Thinking
36 Videos
- THERMOMETRY, THERMAL EXPANSION AND CALORIMETRY BOOK - ERRORLESS CHAPTER - THERMOMETRY, THERMAL EXPANSION AND CALORIMETRY EXERCISE - Self Evaluation Test
15 Videos
- UNITS, DIMENSION & MEASUREMENTSBOOK - ERRORLESS CHAPTER - UNITS, DIMENSION & MEASUREMENTSEXERCISE - All Questions
333 Videos
Similar Questions
Knowledge Check
A block of metal is heated to a temperature of 200∘C which is much higher than the room temperature. It is allowed to cool up to room temperature, in a room which is free from air currents. Its cooling curve (graph of temperature against time) is based on
Aonly Stefan's lawBonly Newton's law of coolingCboth Stefan's law and Newton's law of coolingDneither Stefan's law nor Newton's law but by Kirchoffs lawWhich metal is a liquid at room temperature?
AAluminiumBMercuryCCopperDBrassWhich metal is a liquid at room temperature ?
AHgBKCNaDTi
Which of the following is a liquid metal at room temperature?
View SolutionWhich of the following is a liquid non metal at room temperature
View SolutionA piece of glass is heated to a high temperature and then allowed to cool. If it cracks, a probable reason for this is the following property of glass
View SolutionA non-metal which is gas at room temperature
View SolutionWhen a sphere, a cube and a thin plate are heated to same temperature and then allowed to cool, the first to cool is
View Solution