A triangular loop ABC of string is passed over two small frictionless pulleys A and B. AB=2landBC=AC=ηl. Two masses m and M are attached to the mid-point O of AB and C respectively and m is released. Find the condition that m and M may cross each other.
Step by step video & image solution for A triangular loop ABC of string is passed over two small frictionless pulleys A and B. AB = 2l and BC = AC = eta l. Two masses m and M are attached to the mid-point O of AB and C respectively and m is released. Find the condition that m and M may cross each other. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - NN GHOSHCHAPTER - FRICTION, WORK POWER AND ENERGYEXERCISE - Exercises (A)15videos
FRICTION, WORK POWER AND ENERGY
- BOOK - NN GHOSHCHAPTER - FRICTION, WORK POWER AND ENERGYEXERCISE - Exercises (B)36videos
FRICTION, WORK POWER AND ENERGY
- BOOK - NN GHOSHCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - All Questions39videos
FIRST LAW OF THERMODYNAMICS
- BOOK - NN GHOSHCHAPTER - GRAVITATIONEXERCISE - EXERCISE29videos
GRAVITATION
Similar Questions
Knowledge Check
- Question 1 - Select One
L and M are the mid points of AB and BC respectively of ΔABC , right angled at B . 4LC2=
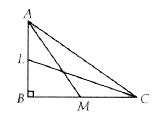 AAB2+4BC2BBC2+4AB2CAC2+4AB2DNone of these
AAB2+4BC2BBC2+4AB2CAC2+4AB2DNone of these - Question 2 - Select One
If ABC is a right angled triangle at B and M, N are the mid-points of AB and BC, then 4(AN2+CM2) is equal to :
A4AC2B6AC2C5AC2D54AC2 - Question 3 - Select One
Two blocks of masses m and 2m are connected by a light string passing over a frictionless pulley. As shown in the figure, the mass m is placed on a smooth inclined plane of inclination 30° and 2m hangs vertically. If the system is released, the blocks move with an acceleration equal to :
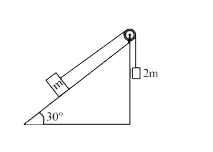 Ag/4Bg/3Cg/2Dg
Ag/4Bg/3Cg/2Dg
ABCD is a parallelogram. L and M are respectively mid points of sides AB and DC. Prove that LD and MB trisects diagonals AC.
View SolutionTwo blocks each of mass m are connected over two light and frictionless pulleys and a fixed wedge by a light string as shown in figure. The tension in the string is :
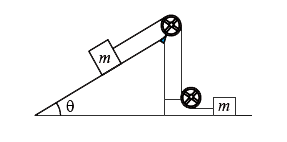 View Solution
View SolutionIn the figure AL, BM and BC are the tangents on the circle at point L, M and P respectively. If AB=1cm and ∠ABC=60∘ find the radius of the circle.
View SolutionA thin uniformed rod of mass m and length L is hinged at one end and from other end a light string is attached. The string is wound over a frictionless pullely (having mass 2m) and a block of mass 2m is connected to string on other side of pulley as shown. the system is released from rest when the rod id making an angle of 37∘ with horizontal. Based on above information answer the following question :
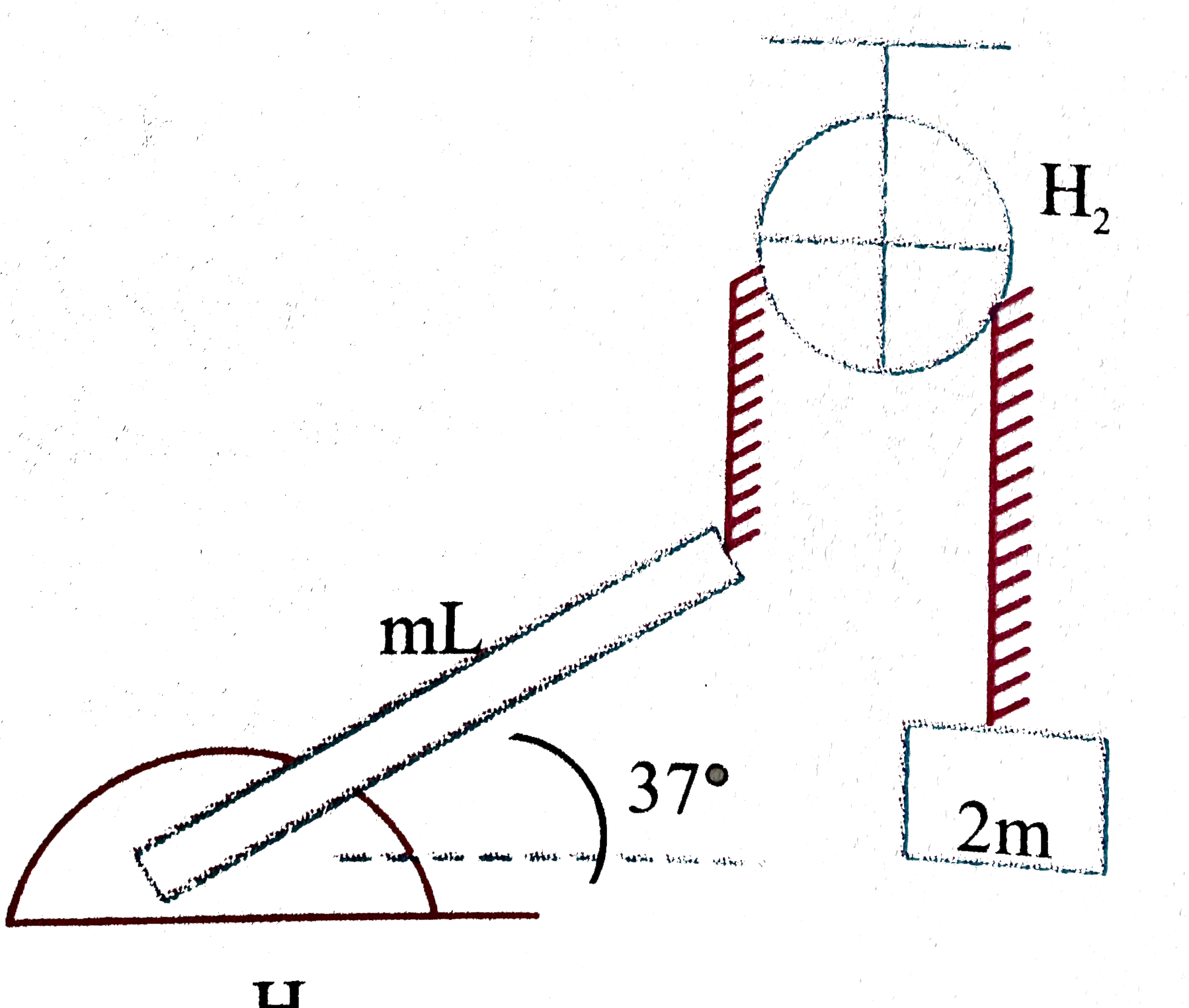
Just after releases of the system from rest acceleration of block isView SolutionTwo masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)
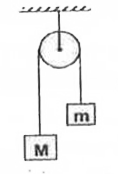 View Solution
View Solution

