
The graph of the function f, dedined by f(x)=−2(x−3)2−4, is shown in the xy-plane above. The function g (not shown) is defined by g(x)=2x−10. If f©=g©, what is one possible value of c ?
−6
−4
2
4
The correct Answer is:C
Because the question states that f(c)=g(c), set the two functions equal to each other and solve for x. To make calculations easier, begin by converting f (x) into standard form:
−2(x−3)2−4
=−2(x−3)(x−3)−4
=−2(x2−6x+9)−4
=−2x2+12x−18−4
=−2x2+12x−22
Now set the two functions equal:
−2x2+12x−22=2x−10
Simpligy by dividing all terms by −2:
x2−6x+11=−x+5
x2−5x+6=0
(x−2)(x−3)=0
Therefore,x=2orx=3, which means that c could also be either 2 or 3. Because 3 is not an answer choice, the answer must be 2. (C ) is correct.
Topper's Solved these Questions
- QUADRATICSBOOK - KAPLANCHAPTER - QUADRATICSEXERCISE - SOLVING QUADRATICS BY FACTORING
1 Videos
- QUADRATICSBOOK - KAPLANCHAPTER - QUADRATICSEXERCISE - CLASSIC QUADRATICS
1 Videos
- QUADRATICSBOOK - KAPLANCHAPTER - QUADRATICSEXERCISE - SYSTEMS OF QUADRATIC AND LINEAR EQUATIONS
1 Videos
- PAIRED PASSAGES AND PRIMARY SOURCE PASSAGES BOOK - KAPLANCHAPTER - PAIRED PASSAGES AND PRIMARY SOURCE PASSAGES EXERCISE - HOW MUCH HAVE YOU LEARNED
11 Videos
- SAT MATH: TIMING ANS SECTION MANAGEMENT STRATEGIESBOOK - KAPLANCHAPTER - SAT MATH: TIMING ANS SECTION MANAGEMENT STRATEGIESEXERCISE - TRY ON YOU OWN
5 Videos
Similar Questions
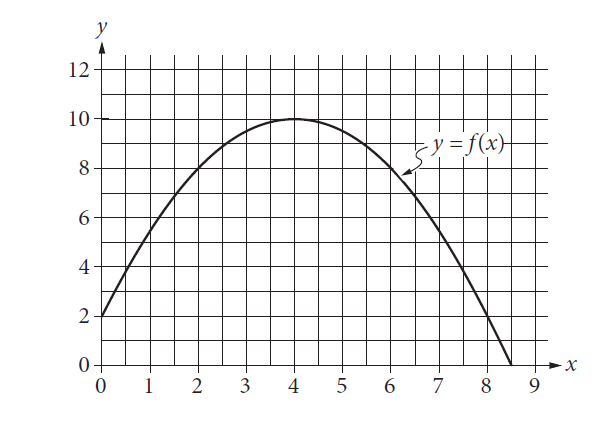
The graph of the function f, defined by f(x)=−12(x−4)2+10, is shown in the xy-plane above. If the function g (not shown) is defined by g(x) = −x + 10, what is one possible value of a such that f (a) = g(a) ?
View Solution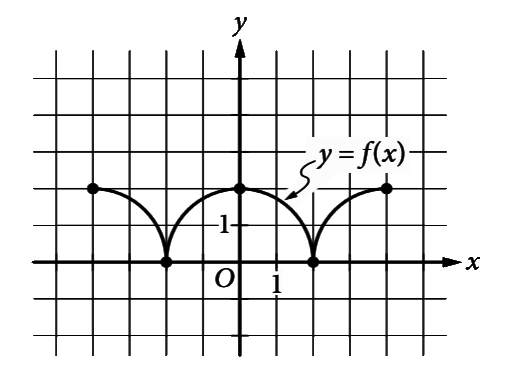
The figure above shows the complete graph of the function f in the xy-plane. The function g (not shown) is defined by g(x) = f (x) + 6.What is the maximum value of the function g ?
View Solution
Knowledge Check
The function f and g are defined as f(x,y)=2x+yandg(x,y)=x+2y. What is the value of f(3,4) ?
Af(4,3)Bf(3,7)Cf(7,4)Dg(4,3)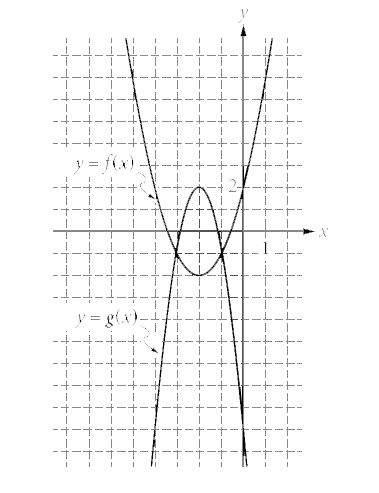
Graphs of the functions f and g are shown in the xy-plane above. For which of the following values of x does f(x)+g(x)=0 ?A−3B−2C−1D0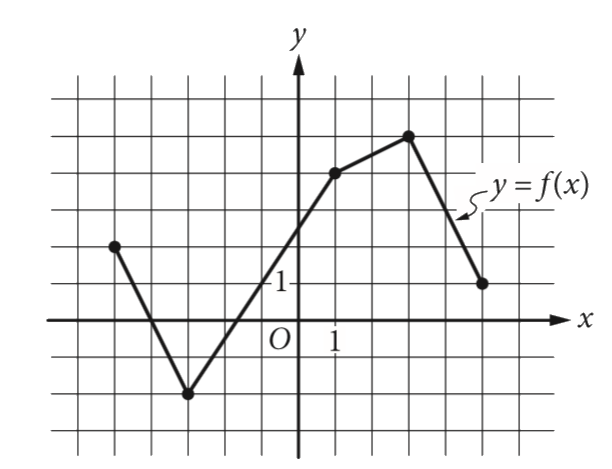
The complete graph of the function f is shown in the xy-plane above. For what value of x is the value of f(x) at its minimum?A−5B−3C−2D3
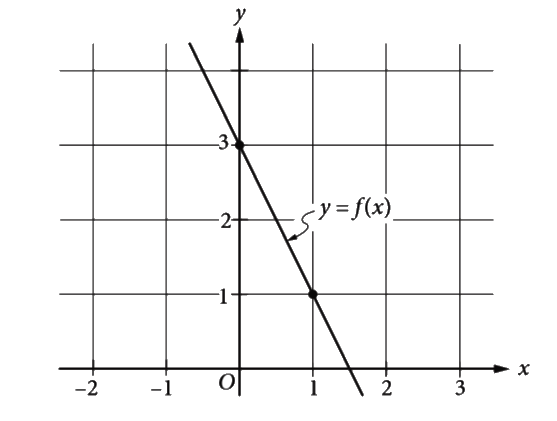
The graph of the linear function f is shown in the xy-plane above. The graph of the linear function g (not shown) is perpendicular to the graph of f and passes through the point (1,3). What is the value of g(0) ?
View SolutionLet f and g be real functions define by f(x)=x+2 and g(x)=4−x2. Then, find each of the following function: f−g
View SolutionLet f and g be real functions define by f(x)=x+2 and g(x)=4−x2. Then, find each of the following function: f+g
View SolutionLet f and g be real functions define by f(x)=x+2 and g(x)=4−x2. Then, find each of the following function: fg
View SolutionLet f and g be real functions define by f(x)=x+2 and g(x)=4−x2. Then, find each of the following function: fg
View Solution
