{a=b2+4b−12a=−12+b
The ordered pair (a,b) satisfies the system of equatin above. What is one possible value of b ?
−6
−3
2
3
The correct Answer is:B
To solve the system of equations given by:
1. a=b2+4b−12
2. a=−12+b
we can set the two expressions for a equal to each other since they both represent a:
b2+4b−12=−12+b
Step 1: Simplify the equation
First, we can eliminate −12 from both sides:
b2+4b−12+12=b
This simplifies to:
b2+4b=b
Step 2: Rearrange the equation
Next, we will move all terms to one side of the equation:
b2+4b−b=0
This simplifies to:
b2+3b=0
Step 3: Factor the equation
Now we can factor the left-hand side:
b(b+3)=0
Step 4: Solve for b
Setting each factor equal to zero gives us:
1. b=0
2. b+3=0 which simplifies to b=−3
Conclusion
Thus, one possible value of b is:
b=−3
2. a=−12+b
First, we can eliminate −12 from both sides:
Next, we will move all terms to one side of the equation:
Now we can factor the left-hand side:
Setting each factor equal to zero gives us:
2. b+3=0 which simplifies to b=−3
Thus, one possible value of b is:
Topper's Solved these Questions
- QUADRATICSBOOK - KAPLANCHAPTER - QUADRATICSEXERCISE - SOLVING QUADRATICS BY FACTORING
1 Videos
- QUADRATICSBOOK - KAPLANCHAPTER - QUADRATICSEXERCISE - CLASSIC QUADRATICS
1 Videos
- QUADRATICSBOOK - KAPLANCHAPTER - QUADRATICSEXERCISE - SYSTEMS OF QUADRATIC AND LINEAR EQUATIONS
1 Videos
- PAIRED PASSAGES AND PRIMARY SOURCE PASSAGES BOOK - KAPLANCHAPTER - PAIRED PASSAGES AND PRIMARY SOURCE PASSAGES EXERCISE - HOW MUCH HAVE YOU LEARNED
11 Videos
- SAT MATH: TIMING ANS SECTION MANAGEMENT STRATEGIESBOOK - KAPLANCHAPTER - SAT MATH: TIMING ANS SECTION MANAGEMENT STRATEGIESEXERCISE - TRY ON YOU OWN
5 Videos
Similar Questions
Knowledge Check
If ab4=16 for positive integers a and b, what is one possible value of b ?
A3B1/2C4D20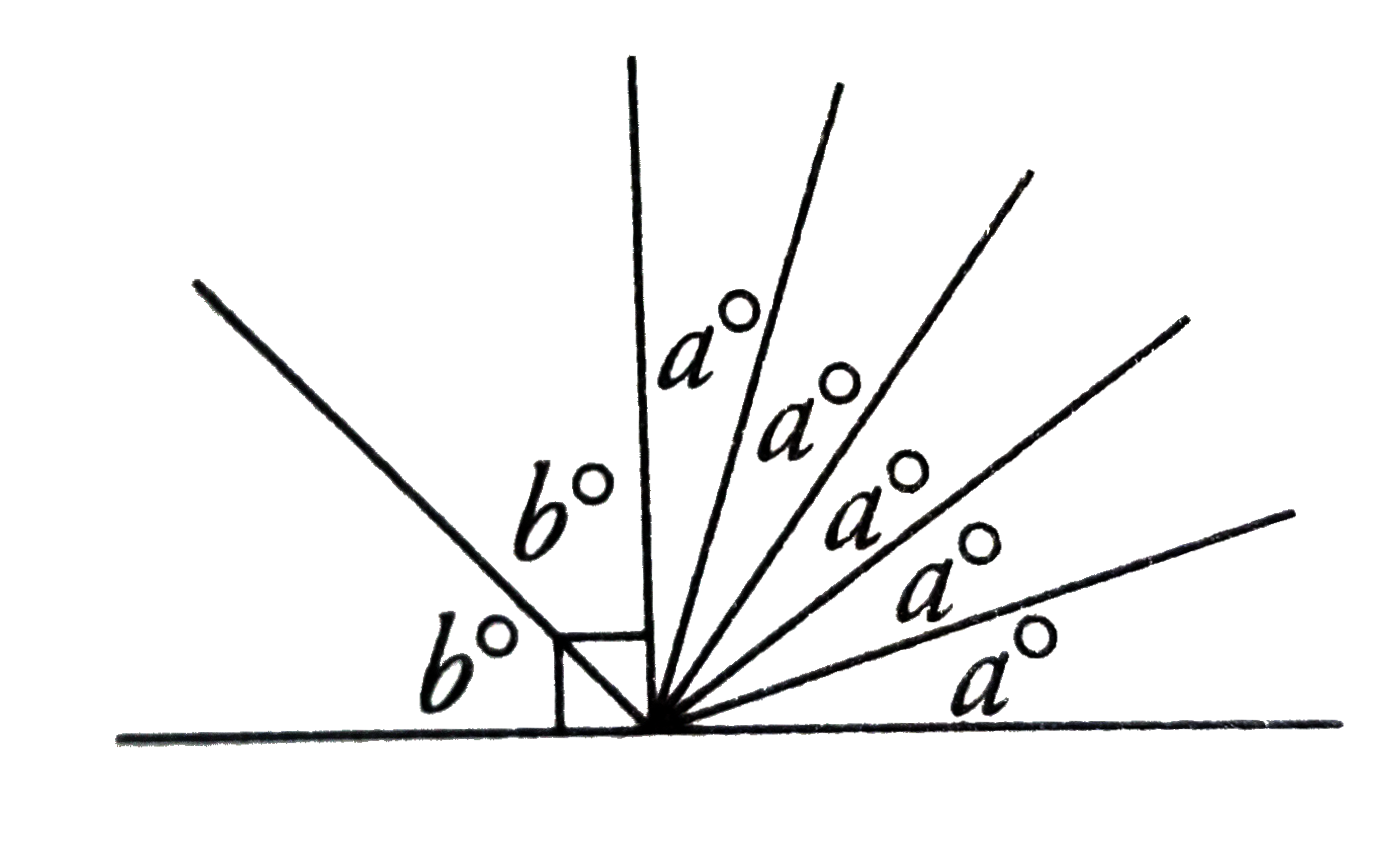
In the figure above, what is the value of 4a-b?A18∘B27∘C45∘D54∘If ab=2, what is the value of 4ba ?
A0B1C2D4
4a−b=−2.25,a+b4.25
If (a, b) satisfies the system of equations above, what is the valeu of a?
View Solutionk=a−b+12,k=b−c−17,k=c−a+11
In the system of equations above, what is the value of k?
View SolutionIf (a, b) is a point in the solution region for the system of inequalities shown above and a=6, what is the minimu possible value of b?
√2⋅x56⋅x3√x
View SolutionIF ab=4 and 3b=2, what is the value of a?
View SolutionIf a-b=12 and b2=10, what is the value of a+b ?
View Solution
