A toy rocket is fired from ground level. The height of the rocket with respect to time can be represented by a quadratic function. If the toy rocket reaches a maximum height of 34 feet 3 seconds after it was fired, which of the following functions could represent the height, h, of the rocket t secnds after it was fired ?
The correct Answer is:A
To solve the problem, we need to represent the height of the toy rocket as a quadratic function based on the information given. The maximum height of the rocket is 34 feet, and it occurs 3 seconds after it is fired from the ground.
1. Understanding the Quadratic Function:
The height h(t) of the rocket can be modeled by a quadratic function in the standard form:
h(t)=a(t−h)2+k
where (h,k) is the vertex of the parabola. Since the rocket reaches a maximum height, the parabola opens downwards, meaning a<0.
2. Identifying the Vertex:
From the problem, we know that the maximum height (the vertex) is 34 feet at t=3 seconds. Thus, we can identify:
h=3andk=34
3. Substituting into the Function:
Plugging these values into the vertex form of the quadratic function, we have:
h(t)=a(t−3)2+34
4. Determining the Value of a:
The problem states that the rocket is fired from ground level, which means when t=0, h(0)=0. We can use this information to find a:
0=a(0−3)2+34
0=9a+34
9a=−34
a=−349
5. Final Function:
Substituting a back into the equation gives us:
h(t)=−349(t−3)2+34
6. Choosing the Correct Option:
We need to check which of the given options matches our derived function. The function must have a negative leading coefficient and should pass through the points we calculated.
The height h(t) of the rocket can be modeled by a quadratic function in the standard form:
h(t)=a(t−h)2+k
where (h,k) is the vertex of the parabola. Since the rocket reaches a maximum height, the parabola opens downwards, meaning a<0.
From the problem, we know that the maximum height (the vertex) is 34 feet at t=3 seconds. Thus, we can identify:
h=3andk=34
Plugging these values into the vertex form of the quadratic function, we have:
h(t)=a(t−3)2+34
The problem states that the rocket is fired from ground level, which means when t=0, h(0)=0. We can use this information to find a:
0=a(0−3)2+34
0=9a+34
9a=−34
a=−349
Substituting a back into the equation gives us:
h(t)=−349(t−3)2+34
We need to check which of the given options matches our derived function. The function must have a negative leading coefficient and should pass through the points we calculated.
Topper's Solved these Questions
- BOOK - KAPLANCHAPTER - QUADRATICSEXERCISE - SOLVING QUADRATICS BY FACTORING1videos
QUADRATICS
- BOOK - KAPLANCHAPTER - QUADRATICSEXERCISE - CLASSIC QUADRATICS1videos
QUADRATICS
- BOOK - KAPLANCHAPTER - QUADRATICSEXERCISE - SYSTEMS OF QUADRATIC AND LINEAR EQUATIONS1videos
QUADRATICS
- BOOK - KAPLANCHAPTER - PAIRED PASSAGES AND PRIMARY SOURCE PASSAGES EXERCISE - HOW MUCH HAVE YOU LEARNED11videos
PAIRED PASSAGES AND PRIMARY SOURCE PASSAGES
- BOOK - KAPLANCHAPTER - SAT MATH: TIMING ANS SECTION MANAGEMENT STRATEGIESEXERCISE - TRY ON YOU OWN5videos
SAT MATH: TIMING ANS SECTION MANAGEMENT STRATEGIES
Similar Questions
If x2−7x=30andx>0, what is the value of x−5 ?
02:43View SolutionWhich of the following expressions is equivalent to 25x2y4−1 ?
05:13View SolutionIn the xy-plane, the graph of y+3x=5x2+6andy−6=2x intersect at points (0,6) and (a,b). What is the value of b ?
05:25View SolutionPassage 1 is adapted from an 1823 speech by president james Monre, in which he discusses European colonialism in the Americas. The position expressed in this speech would eventually become known as the Monroe Doctrine. Passage 2 is adapted from a 1095 speech by President Theodore Roosevelt. His position would become known as the Roosevelt Corollary to the Monroe Doctrine.
Passage 1
The American continents, by the free and independent cnditin which they have assumed and maintain, are hence forth not to be considered as subjects for future colonization by any European powers. The citizens of the United States cherish friendaly sentiments in favor of teh liberty and happiness of their fellow men on the European side of the Atlantic. in the wars of the European powers in matters relating to themselves we have never taken any part, nor does it comport with out policy to do so. It is only when our rights are invarded or seriously menaced that we resent injuries or make preparatin for our defense. With the movements in our own hemisphere we are more immediately connected, by causes which must be obvious to all enlightened and impartial observers.
We owe it, therefore, to candor and to the amicable relations existing between the United States and European nations to declear that we should consider any attempt on their part to extend their system of government to any protion of this hemisphere as dangerous to our peace and safety. With the existing colonies or dependncies of any Wuropean powe we have not interfered and shall not interfere. however, we could not view any middling with those former European colonies who have declared their independence and maintained it, and whose independence we have, on great consideration and on just rinciples, acknowledged, in any other light than as the manifestation of an unfriendly desposition toward the united States.
Passage 2
It isw not true that the united States feels any land hunger or entertains any projects regarding the other nations of the Western Hemisphere except for their welfare. All that this country desires is to see our neighboring countries stable, orderly, and prosperous. Any country whose people conduct themselves well can count upon our hearty friendship. If a nation shows that it knows how to act with reasonalbe efficiency and decency in social and plitical matters, if it keeps order and pays its obligations, it need not fear interference from the United States. However, chronic wrongdoing, or an impotence which results in a general loosening of the ties of civilized society, may in America, as elsewhere, ultimately require intervention.... In thw Western Hempisphere, the adherence of the United States to the Monroe Doctrine may force the United States, however reluctantly, in flagrant cases of such wrongdoing or impotence, to the exercise of an inernational police power. If every country washed by the Caribbean Sea would show the progress in stable and just civilization which Cuba has shown since our troops left the island, and which so many of the republics in both Americas are constantly and brilliantly showing, all question of interference by this Nation with their affairs would be at an end. Our intersets and those of our southern neighbors are in reality identical. They have great natural riches, and if within their borders the reign of law and justice obtains, prosperity is sure to come to them. While they thus obey the primary laws of civilized society, they may rest assured that they will be treated by us in a spirit of cordial and helpful sympthy. We would interfere with them only in the last resort, and then only if it became evident that their inability or unwillingness to do justic at home and abroad had violated the rights of the United States or had invited foreign aggression to the determent of the entire body of American nations. Every nation, whether in America or anywhere else, which desires to maintain its freedom and independence must ultimately realize that the right of such independence can not be separated from the respondibility of making good use of it.
The primary purpose of the statement in lines 6-9 ("The citizens ...of the Atlantic") is to01:40View SolutionIf 79x−16x=13+12, what is the value of x ?
03:49View SolutionThe graph shown the variation of velocity of a rocket with time. Then, the maximum height attained by the rocket is.
03:34View SolutionMaximum height reached by a rocket fired with a speed equal to 50% of the escape velocity from earth's surface is:
06:03View SolutionA rocket is fired upward from the earth's surface such that it creates an acceleration of 19.6 m/sec . If after 5 sec its engine is switched off, the maximum height of the rocket from earth's surface would be
03:04View SolutionA rocket is fired upwards. Its velocity versus time graph is shown in the figure-1.131. The maximum height reached by the rocket is:
02:32View SolutionA rocket is fired vertically from the ground. It moves upwards with a constant acceleration 10m/s2 after 30 sec the fuel is finished. After what time from the instant of firing the rocket will attain the maximum height? g=10m/s2:-
05:20View Solutionएक रॉकेट ऊपर की और इस प्रकार दागा जाता है की इसका इंजन पूर्णतया सक्रिय होने में 10 सेकण्ड लेता है । इसका वेग-समय आरेख संलग्न चित्र में दिखाया गया है । रॉकेट द्वारा प्राप्त ऊँचाई है :
 08:16View Solution
08:16View Solutionh(t)=−4.9t2+68.6t
The function above gives the height of a model rocket, in meters, t seconds after it is launched from ground level. What is the maximum height, to the nearest meter, attained by the model rocket?06:08View SolutionA model rocket is launched from the ground. The height 'h' reached by the rocket after t seconds from lift off is given by h(t) = -5t2+100t,0≤t≤20. At what time the rocket is 495 feet above the ground?
02:44View SolutionA rocket is fired upwards, its engine explodes fully in 12 s. The height reached by the rocket as calculated from its velocity - time graph is
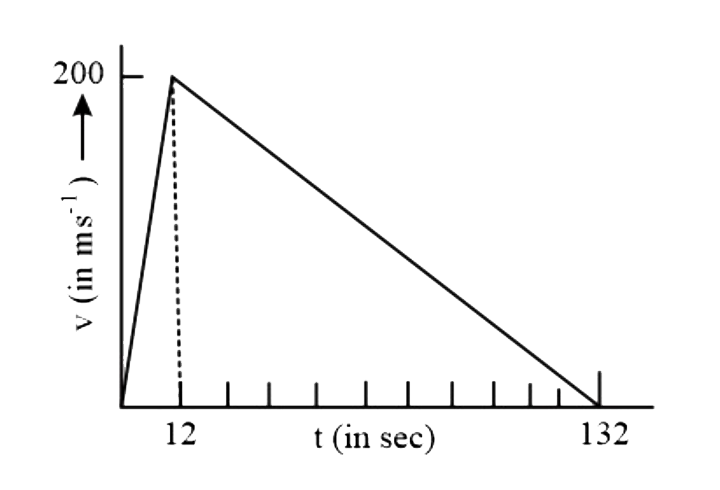 02:31View Solution
02:31View SolutionA rocket is fired vertically upwards with an acceleration. 10 "m.s"^(-2) . To what maximum height would the rocket rise if its fuel gets exhausted in 1 min?
04:31View Solution

