The function f(x)=4x2−25andg(x)=−4x2+25 are graphed in the xy-plane above. The point where the two functions intersect are (z,0) and (−z,0). What is the value of z ?
0.5
1.0
2.5
4.0
The correct Answer is:C
To find the value of z where the functions f(x)=4x2−25 and g(x)=−4x2+25 intersect, we need to set the two functions equal to each other and solve for x.
1. Set the Functions Equal:
f(x)=g(x)
This gives us the equation:
4x2−25=−4x2+25
2. Combine Like Terms:
Move all terms involving x2 to one side and constant terms to the other side:
4x2+4x2=25+25
Simplifying this, we get:
8x2=50
3. Divide by 8:
To isolate x2, divide both sides by 8:
x2=508
Simplifying the fraction:
x2=254
4. Take the Square Root:
To find x, take the square root of both sides:
x=±√254
This simplifies to:
x=±52
5. Identify the Value of z:
Since the points of intersection are (z,0) and (−z,0), we take the positive value:
z=52=2.5
Final Answer:
The value of z is 2.5.
f(x)=g(x)
This gives us the equation:
4x2−25=−4x2+25
Move all terms involving x2 to one side and constant terms to the other side:
4x2+4x2=25+25
Simplifying this, we get:
8x2=50
To isolate x2, divide both sides by 8:
x2=508
Simplifying the fraction:
x2=254
To find x, take the square root of both sides:
x=±√254
This simplifies to:
x=±52
Since the points of intersection are (z,0) and (−z,0), we take the positive value:
z=52=2.5
The value of z is 2.5.
Topper's Solved these Questions
- BOOK - KAPLANCHAPTER - QUADRATICSEXERCISE - SOLVING QUADRATICS BY FACTORING1videos
QUADRATICS
- BOOK - KAPLANCHAPTER - QUADRATICSEXERCISE - CLASSIC QUADRATICS1videos
QUADRATICS
- BOOK - KAPLANCHAPTER - QUADRATICSEXERCISE - SYSTEMS OF QUADRATIC AND LINEAR EQUATIONS1videos
QUADRATICS
- BOOK - KAPLANCHAPTER - PAIRED PASSAGES AND PRIMARY SOURCE PASSAGES EXERCISE - HOW MUCH HAVE YOU LEARNED11videos
PAIRED PASSAGES AND PRIMARY SOURCE PASSAGES
- BOOK - KAPLANCHAPTER - SAT MATH: TIMING ANS SECTION MANAGEMENT STRATEGIESEXERCISE - TRY ON YOU OWN5videos
SAT MATH: TIMING ANS SECTION MANAGEMENT STRATEGIES
Similar Questions
Knowledge Check
- Question 1 - Select One
f(x)=x2−6x+8 and g(x)=x−2 . At how many points do the graphs of the two functions intersect ?
A0B1C2D3 - Question 2 - Select One
The function f is defined by f(x)=x4−4x4−x2+cx−12 , where c is a constant.In the xy-plane, the graph of f intersects the x-axis in the four points (-2,0), (1,0), (p,0), and (q,0). What is the value of c ?
A16B−16CpqDqp - Question 3 - Select One
f(x)=3x3+kx2−32x+28
The function f is defined by the equation above where k is a nonzero constant. In the xy-plane the graph of f intersects the x-axis at three points: (−2,0),(32,0),and(c,0). What is the value of k?A−25B−17C7D14
In the xy-plane the point (2,5) lies on the graph of the function f. IF f(x) =k−x2 where k is a constant, what is the value of k?
View Solutiong(x)=x4−kx3+13x2−12x+4
The function g is defined above, and k is a constant. In the xy- plane, the graph of g intersects the y - axis at (0,4) and intersects the x - axis at (1,0) and (2,0). What is the value of k?View Solution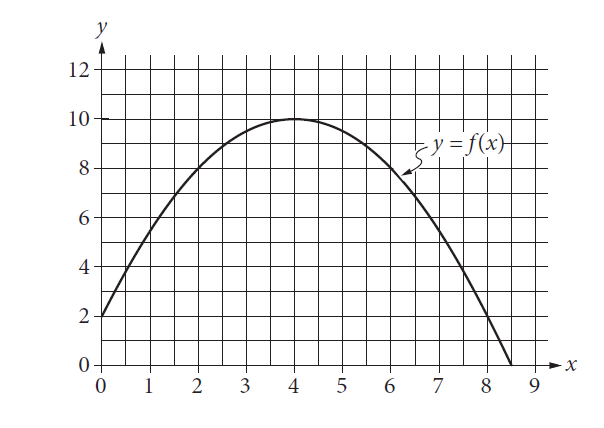
The graph of the function f, defined by f(x)=−12(x−4)2+10, is shown in the xy-plane above. If the function g (not shown) is defined by g(x) = −x + 10, what is one possible value of a such that f (a) = g(a) ?View Solution
a quandratic function and a linear function are graphed in the xy-plane as shown above. The vertex of the graph of the quadratic function is at (3,25). If the two graphs intersect in the first quadrant at the point (j,k) what is the value of the product jk?View SolutionThe polynomial function p is defined by p(x)=4x3+bx2+41x+12, where b is a constant. When graphed on a standard coordinate plane, p intersects the x-axis at (−0.25,0),(3,0)and(k,0). What is the value of b?
View Solution

