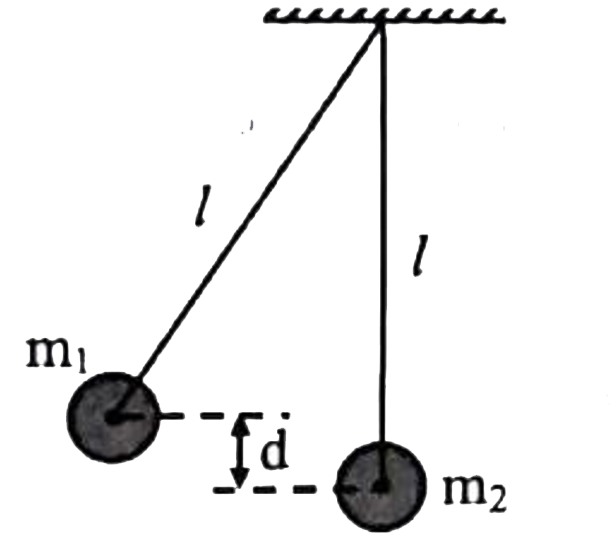
Two pendulums each of lengh l are initially situated as shown in figure. The first pendulum is released and strikes the second. Assume that the collision is completely inelastic and neglect the mass of the string and frictional effects. How high does the centre of mass rise after the collision ?
d[m1(m1+m2)]2
d[m1(m1+m2)]
d(m1+m2)2m2
d[m2(m1+m2)]2
The correct Answer is:A
By conservation of momentum
m1v1=(m1+M2)V
orm1√2gd=(m1+m2)v
let centre of mass rise through a height h
12(m1+m2)v2=(m1+m2)gh
h=d{m1m1+m2}2
Topper's Solved these Questions
Similar Questions
Two balls having masses m and 2m are fastened to two light strings of same length l figure. The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. a. Find velocities of the balls just after their collision. b. How high will the balls rise after the collision.

View SolutionA particle of mass m strikes a disc of radius R and mass m with a speed u as shown in the figure. What is the speed of the particle just after the collision if the collision is perfectly inelastic ?
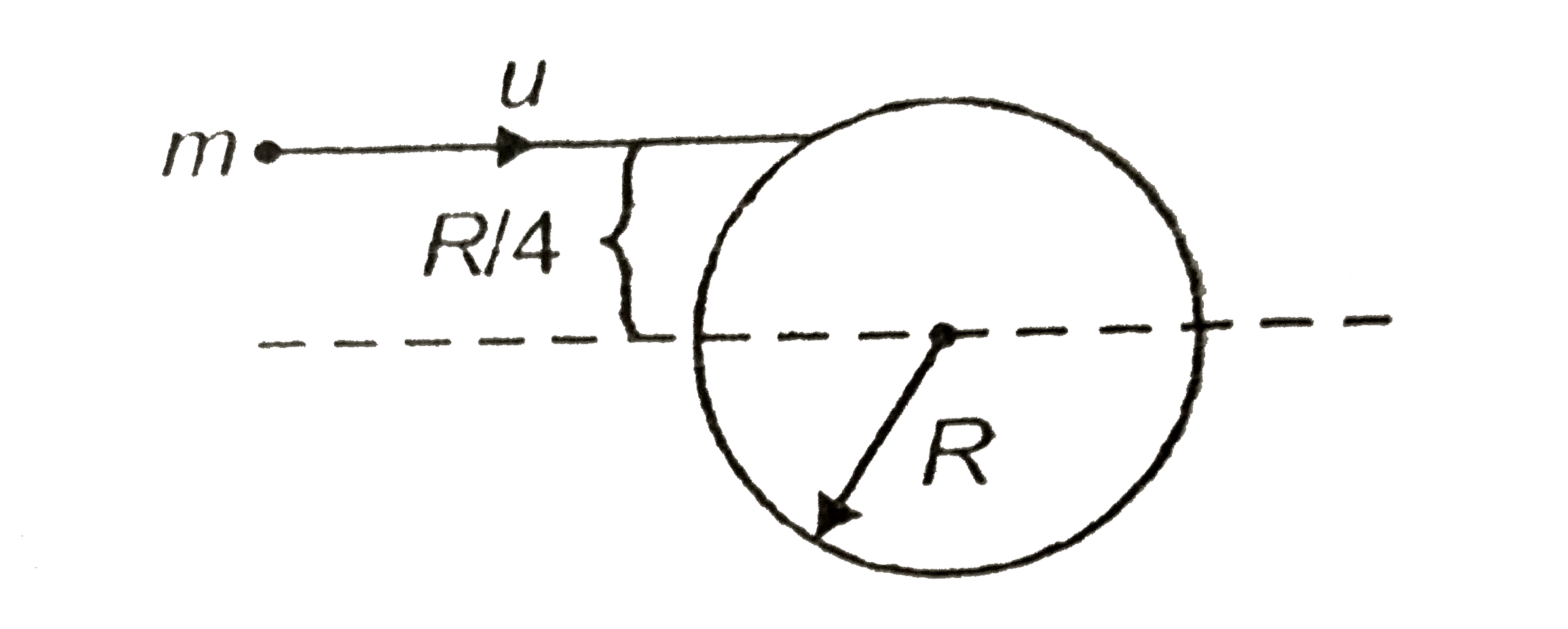
View Solution
Knowledge Check
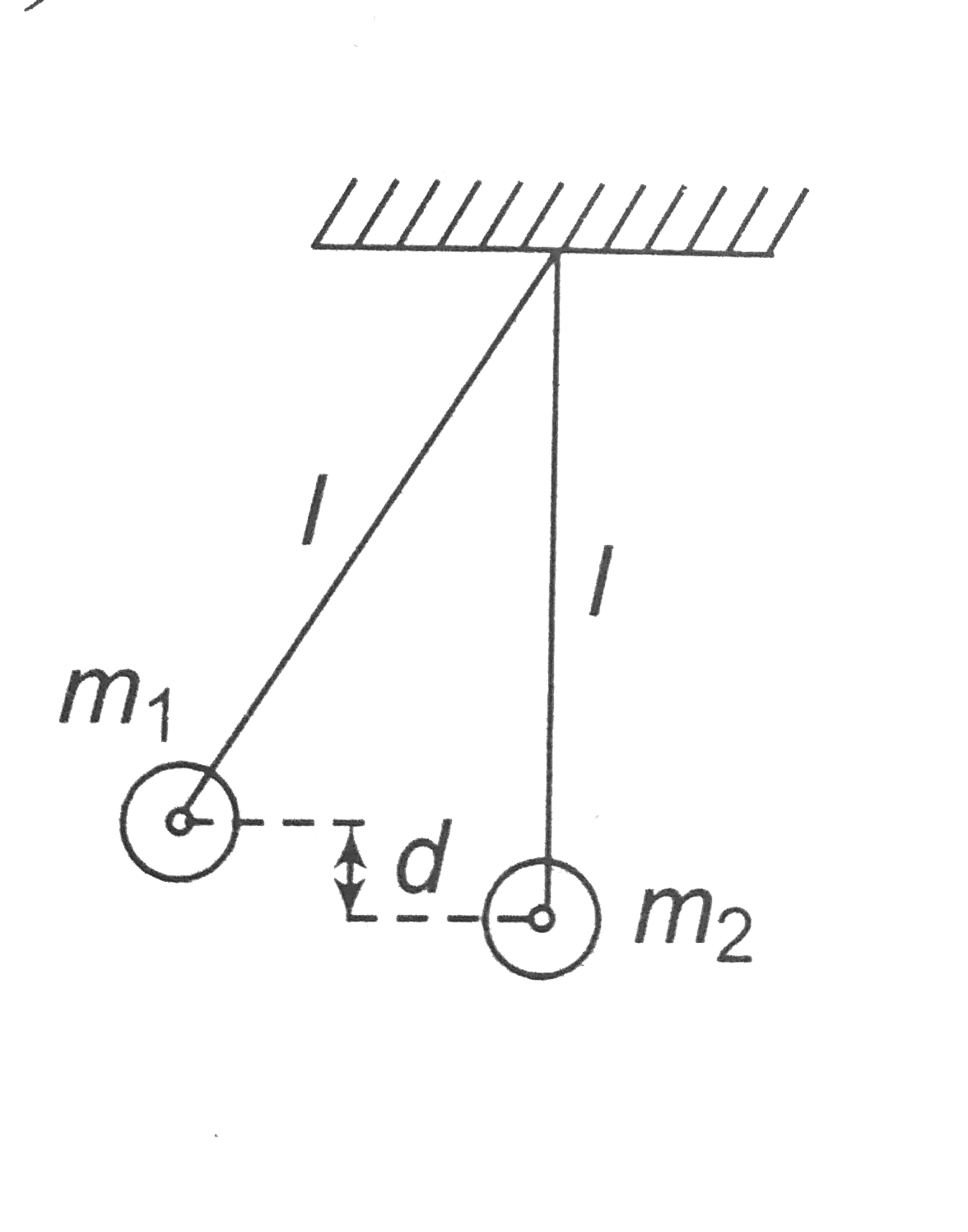
Two pendulums each of length l are initially situated as shown in Fig. The first pendulum is released and strikes the second. Assume that the collision is completely inelastic and neglect the mass of the string and any frictional effects. How high does the centre of mass rise after the collision?
 Ad[m1(m1+m2)]2Bd[m1(m1+m2)]Cd[(m1+m2)m2]2D[m2(m1+m2)]2
Ad[m1(m1+m2)]2Bd[m1(m1+m2)]Cd[(m1+m2)m2]2D[m2(m1+m2)]2Two pendulum each of length l are initial situated as shown in figure. The first pendulum is released and strikes the second . Assume that the collision is completely inelastic and neglect the mass of the string and any frictional effects. How high does the center of mass rise after the collision?
 Ad[m1(m1+m2)]2Bd[m1(m1+m2)]Cd(m1+m2)2m2Dd[m2(m1+m2)]2
Ad[m1(m1+m2)]2Bd[m1(m1+m2)]Cd(m1+m2)2m2Dd[m2(m1+m2)]2A ball of mass m moving horizontally at a speed v collides with the bob of a simple pendulum at rest. The mass of the bob is also m. If the collision is perfectly inelastic and both balls sticks, the height to which the two balls rise after the collision will be given by:
Av2gBv22gCv24gDv28g
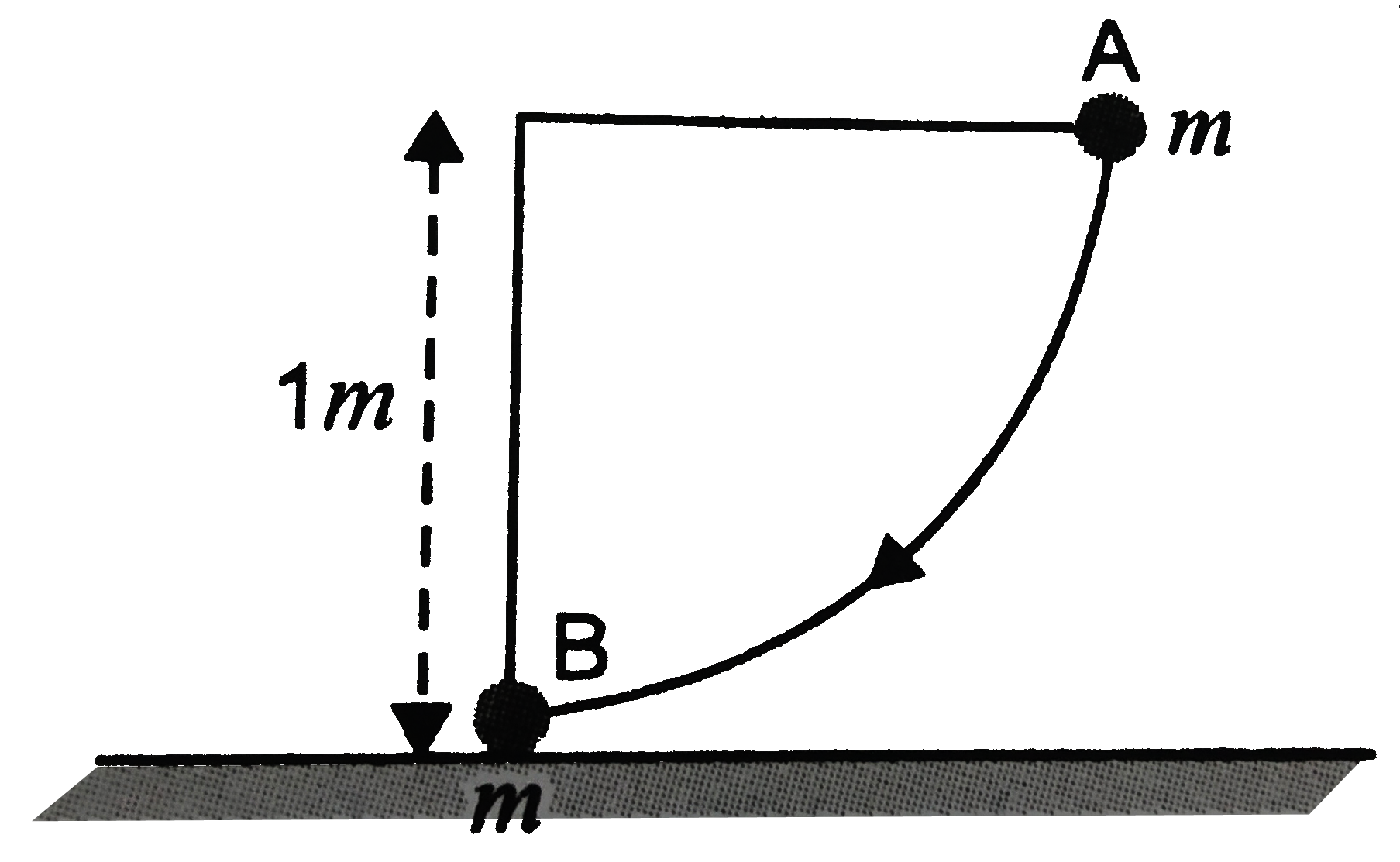
The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
If the length of the pendulum is 1m, calculate
(a) the height to which bob A will rise after collision.
(b) the speed with which bob B starts moving.
Neglect the size of the bobs and assume the collision to be elastic.
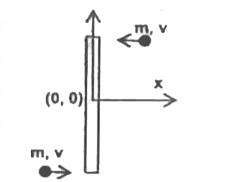
View SolutionA rigid uniform rod of mass M and length L is placed along the Y-axis on a smooth horizontal surface with its centre at the origin. Two particles , each of mas m(=M/12) hits simultaneously , at the two ends with equal speed v as shown in the figure. The collision is completely inelastic.
(i) Find the angular velocity of the system after the collision.
(ii) Two particles of mass 2m and m are placed respectively at ( L/2,0) and (−L/2,0). Calculate the time when the rod hits these particles.
View SolutionTwo massless string of length 5 m hang from the ceiling very near to each other as shown in the figure. Two balls A and B of masses 0.25kg and 0.5kg are attached to the string. The ball A is released from rest at a height 0.45m as shown in the figure. The collision between two balls is completely elastic. Immediately after the collision, the kinetic energy of ball B is 1J The velocity of ball A just after the collision is
Q01.png)
View SolutionTwo massless string of length 5 m hang from the ceiling very near to each other as shown in the figure. Two balls A and B of masses 0.25kg and 0.5kg are attached to the string. The ball A is released from rest at a height 0.45m as shown in the figure. The collision between two balls is completely elastic. Immediately after the collision, the kinetic energy of ball B is 1J The velocity of ball A just after the collision is
Q01.png)
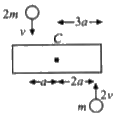
View SolutionA uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving with the same horizontal speed 2v and v respectively, strike the bar as shown in the figure and stick to the bar after collision. Denoting angular velocity (about the centre of mass), total energy, and centre of mass velocity after collision by ω, E and vC respectively, we have after collision
View Solution
