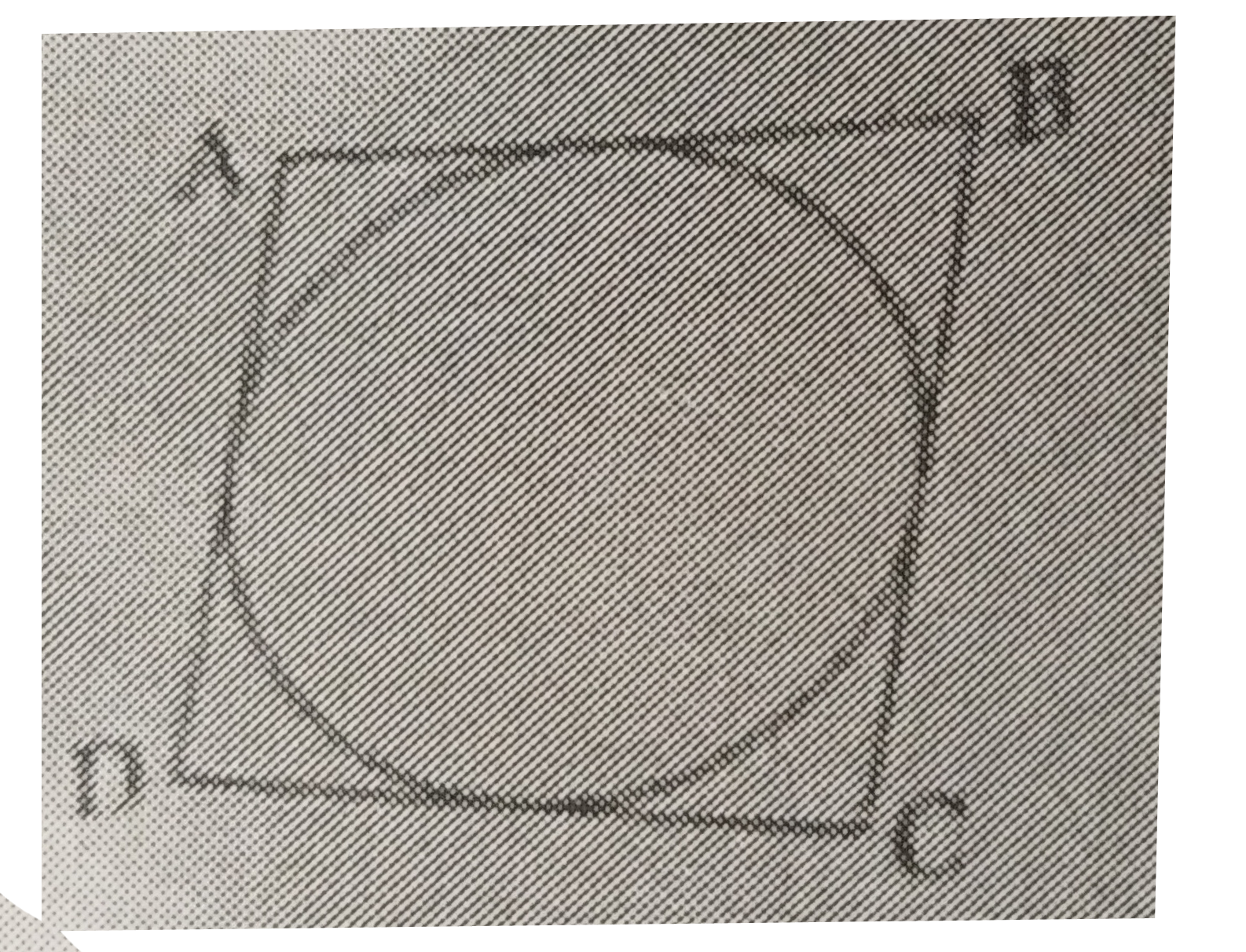
If a hexagon ABCDEF circumscribe a circle, prove that $A B + C D + E F = B C + D E + F A$

Video Solution

Text Solution

Verified by Experts

Given A hexagon ABCDEF circumscirbe a circle.

To prove $A B + C D + E F = B C + D E + F A$
Proof $A B + C D + E F = (A Q + Q B) + (C S + S D) + (E U + U F)$
$= A P + B R + C R + D T + E T + F P$
$= (A P + F P) + (B R + C R) + (D T + E T)$
$A B + C D + E F = A F + B C + D E$ :.AQ=AP
QB=BR
CS=CR
DS=DT
EU=ET
[tangents drawn from an external point to a circle are equal]
Hence proved.

Updated on:21/07/2023