In a right angle triangle $Δ A B C$ is which $∠ B = 90^{\circ}$ a circle is drawn with AB diameter intersecting the hypotenuse AC at P.Prove that the tangent to the circle at PQ bisects BC.

Video Solution

Text Solution

Verified by Experts

Let O be the centre of the given circle. Suppose, the tangent at P meets BC at Q. Join BP.

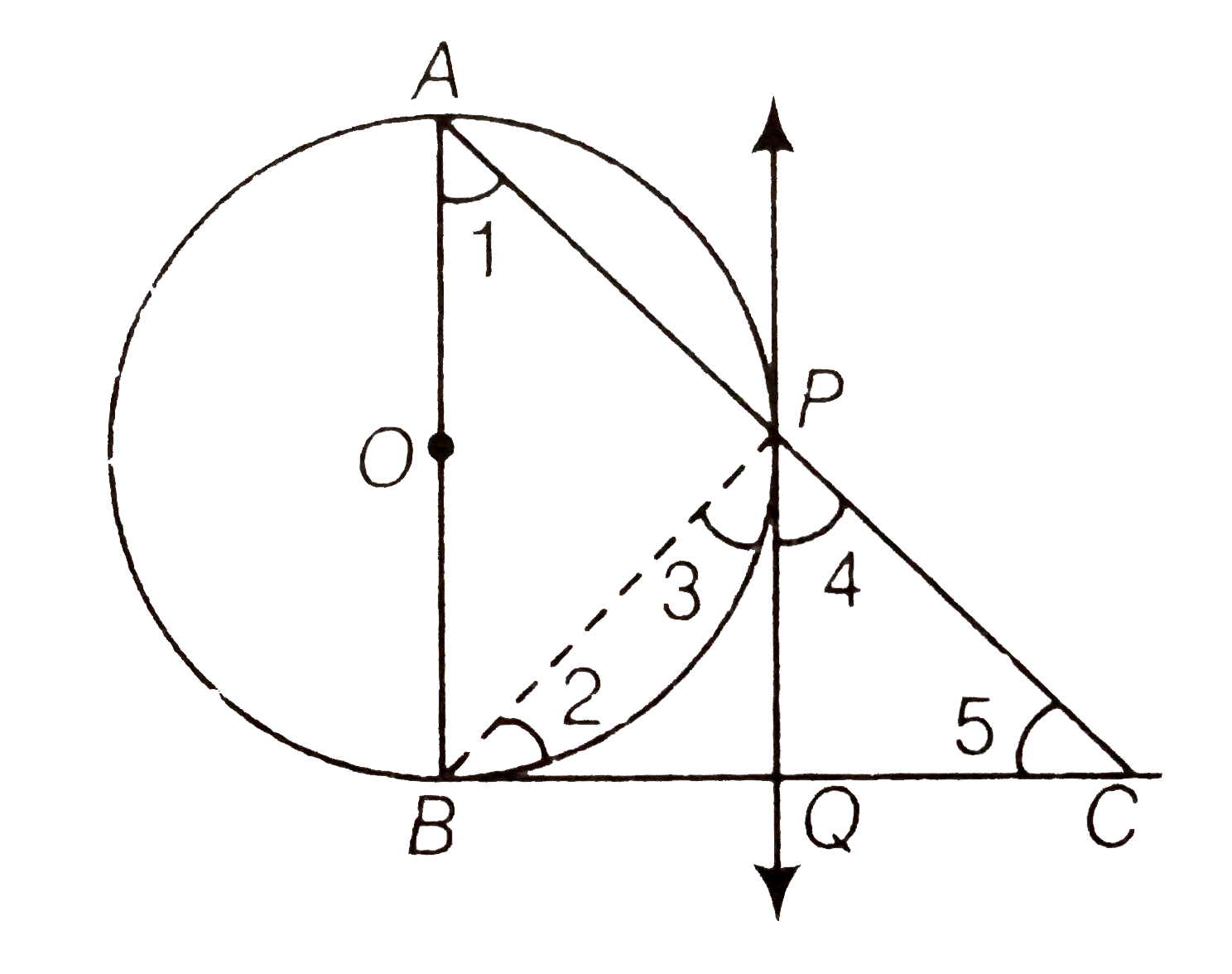
To prove BQ=QC [angles in alternate segment]
Proof $∠ A B C = 90^{\circ}$
[tangent at any point of circle is perpendicular to radius through the point of contact] :.In $Δ A B C$ , $∠ 1 + ∠ 5 = 90^{\circ}$ [angle sum property, [ $∠ A B C = 90^{\circ}$ ]
$∠ 3 = ∠ 1$
[angle between tangent and the chord equals angle made by the chord in alternate segment]
$∴ ∠ 3 + ∠ 5 = 90^{\circ} ... . . (i)$
Also, $∴ ∠ A P B = 90^{\circ}$ [angle in semi-circle]
$\Rightarrow ∠ 3 + ∠ 4 = 90^{\circ}$ $[∠ A P B + ∠ B P C = 180^{\circ}, linera pair]$
From Eqs. (i) and (ii), we get
$∠ 3 + ∠ 5 + ∠ 3 + ∠ 4$
$\Rightarrow ∠ 5 = ∠ 4$
$\Rightarrow P Q = Q C$ [sides opposite to equal angles are equal]
Also, QP=QB
[tangents drawn from an internal point to a circle are equal]
$\Rightarrow Q B = Q C$ Hence proved.

Updated on:21/07/2023