A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ΔABC
12 cm
20 cm
24 cm
30 cm
The correct Answer is:C
Given Two tangents are drawn from an external point A to the circle with centre O.
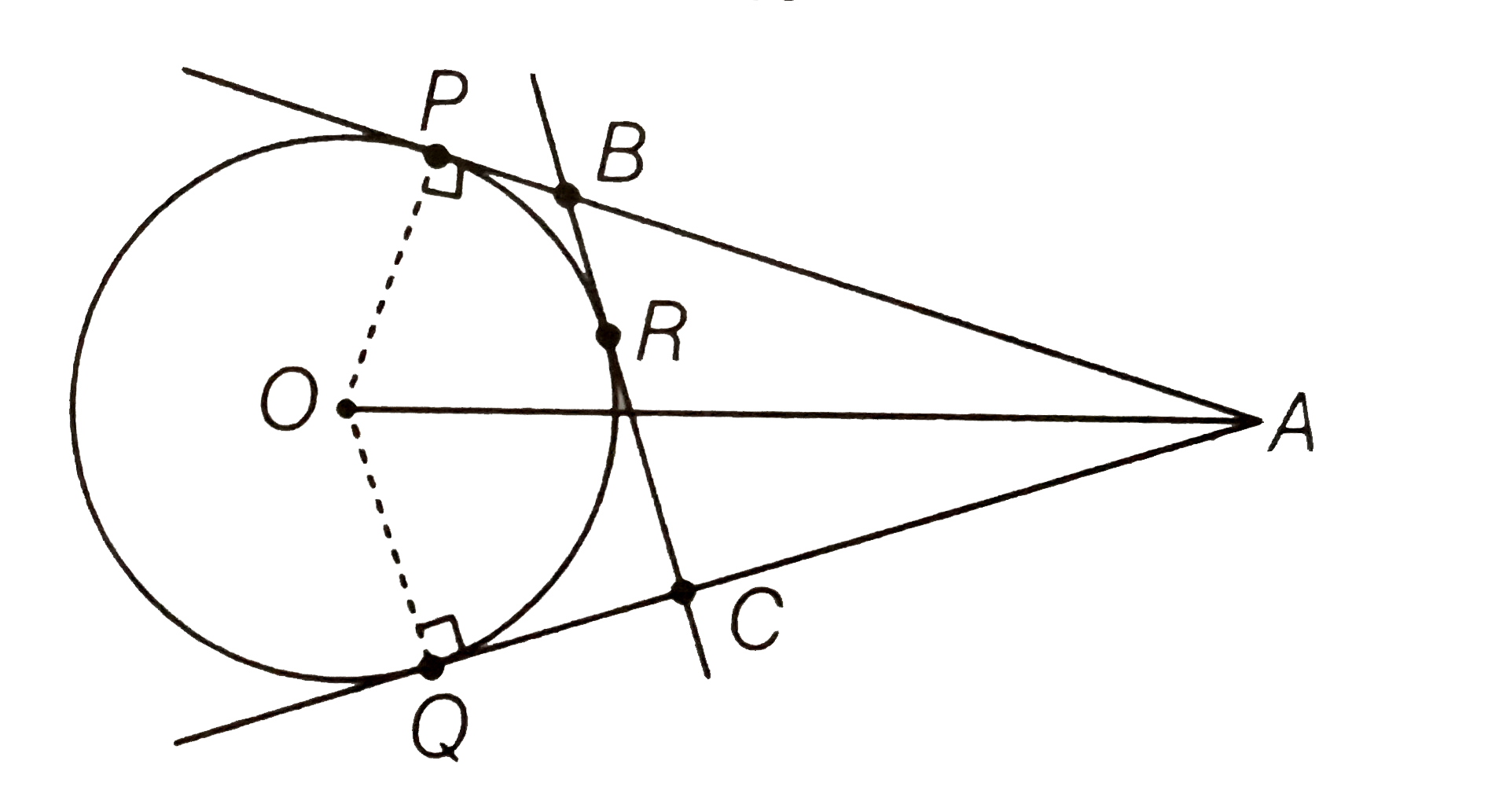
Tangent BC is drawn at a point R. radius of circle equals 5cm.
To find perimeter of ΔABC.
Proof ∠OPA=90∘
[tangent at any point of a circle is perpendicular to the radius through the point of contact]
∴OA2=OP2+AP2 [by Pythagoras theorm]
(13)2=52+PA2
⇒PA2=144=122
⇒PA=12cm
Now, perimeter of ΔABC=AB+BC+CA
=(AB+BR)+(RC+CA)
=AB+BP+CQ+CA
[∵BR=BP,RC=CQ tangents from internal point to a circle are equal]
=AP+AQ
=2AP
=2(12)
=24cm
[AP=AQ tangnet from internal point to a circle are equal]
Hence, the perimeter of ΔABC=24cm.
Topper's Solved these Questions
Similar Questions
A is a point at a distance 10 cm from the centre O of a circle of radius 6cm . AP and AQ are the tangents to the circle at P and Q .If a tangent BC is drawn at a point R lying on the mirror are PQ to intersect AP at B and AQ at C, find the perimeter of the ΔABC .
View SolutionA is a point at a distance 26 cm from the centre O of a circle of radius 10 cm. AP and AQ are the tangents to the circle at the point of contacts P and Q. If a tangent BC is drawn at a point R lying on the minor are PQ to intersect AP at B and AQ at C, then the perimeter of △ABC is:
त्रिज्या 10 सेमी के वृत्त के केंद्र O से 26 सेमी की दूरी पर A एक बिंदु है। AP और AQ बिंदु P और Q पर स्पर्शरेखा है। यदि स्पर्शरेखा BC वृत्त के PQ माइनर को R पर कटती है और PA को B पर और PQ को C पर प्रतिछेदित करती है , तो ABC की परिधि हैView SolutionA is a point at a distance 26 cm from the centre O of a circle of radius 10 cm. AP and AQ are the tangents to the circle at the point of contacts P and Q. If a tangent BC is drawn at a point R lying on the minor are PQ to intersect AP at B and AQ at C, then the perimeter of △ABC is:
त्रिज्या 10 सेमी के वृत्त के केंद्र O से 26 सेमी की दूरी पर A एक बिंदु है। AP और AQ बिंदु P और Q पर स्पर्शरेखा हैं। यदि स्पर्शरेखा BC वृत्त के PQ माइनर को R पर कटती है और PA को B पर और PQ को C पर प्रतिछेदित करती है , तो ABC की परिधि हैView SolutionA point P is at a distance of 29cm from the centre of a circle of radius 20cm. Find the length of the tangent drawn from P to the circle.
View SolutionIf a point P is 17 cm from the centre of a circle of radius 8 cm, then find the length of the tangent drawn to the circle from point P.
View SolutionFrom a point P which is at a distance of 13 cm form the centre of the circle of radius 5 cm, a tangent is drawn to the circle . The length of the tangent is ____________
View SolutionFrom a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Find the area of quadrilateral PQOR,
View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm . Find the radius of the circle.
 View Solution
View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
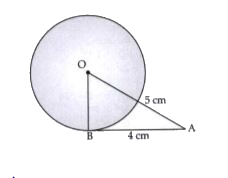 View Solution
View Solution

