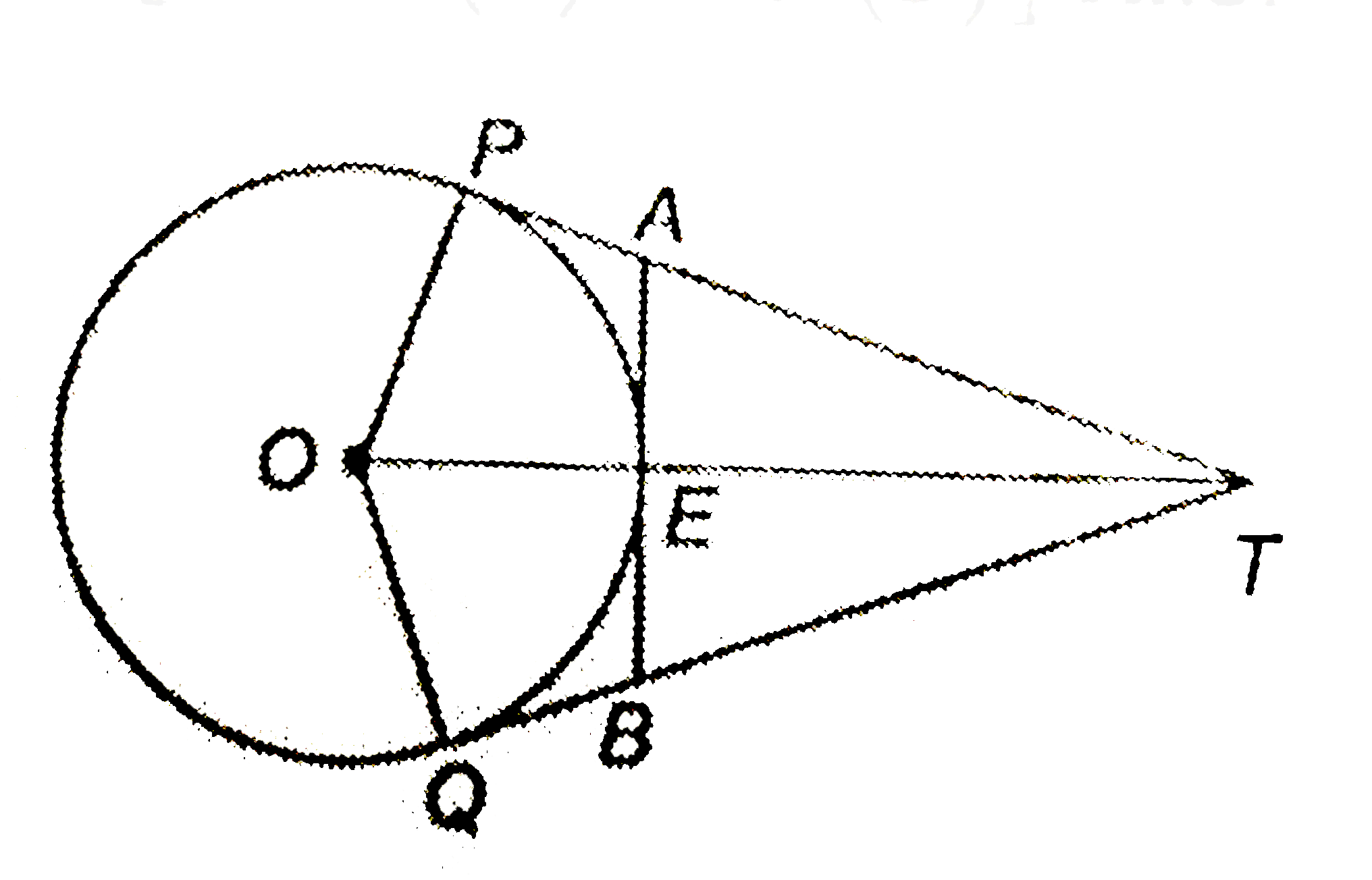
Type V: O is the center of the circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E . If AB is the tangent to the circle at E; find the length of AB.
Given, OT =13cm and OP =5cm
Since, if we drawn a line from the centre to the tangent of the circle. It is always perpendicular to the tangent i.e., OP⊥PT.
In right angled ΔOPT,OT2=OP2+PT2
[by Pythagoras theorem, (hypotenuse)2=(base)2+(perpendicular)2]
⇒PT2=(13)2−(5)2=169−25=144
⇒PT=12cm
Since, the langth of pair of tangents from an external point T is equal.
∴QT=12cm
Now, TA=PT-PA
⇒TA=12−PA.....(i)
and TB=QT-QB
⇒TB=12−QB......(ii)
Again using the property, length of pair of tanagets from an external point is equal.
∴PA=AEandQB=EB.......(iii)
∴OT=13cm
∴ET=OT−OE [∴OE=5cm=radius]
⇒ET=13−5
⇒ET=8cm
Since, AB is a tangent and OE is the radius.
∴OE⊥AB
⇒∠OEA=90∘
∴∠AET=180∘−∠OEA [linear pair]
⇒∠AET=90∘
Now, in right angled ΔAET,
(AT)2=(AE)2+(ET)2 [by Pythagoras theorem]
⇒(PT−PA)2=(AE)2+(8)2
⇒(12−PA)2=(AP)2+(8)2 [from Eq. (iii)]
⇒144+(PA)2−24.PA=(PA)2+64
⇒24.PA=80
⇒PA=103cm
∴AE=103cm [from Eq. (iii)]
Join OQ.
Similarly BE=103cm
Hence, AB=AE+EB
=103+103
=203cm
Hence, the required length AB is =203cm.
Topper's Solved these Questions
Similar Questions
O is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find length of AB.
View SolutionO is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E, find the length AB.
View Solution
Knowledge Check
O is the centre of a circle of radius 5cm. T is a point such that OT=13cmandOT intersects the circle at E. If AB is the tangent to the circle at E, find length of AB.
A20 cmB203cmC10cmD25 cmType V: O is the center of the circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E . If AB is the tangent to the circle at E; find the length of AB.
A103B203C163DCannot be determined
Tangents PT and QT are drawn on a circle of radius 5 cm from point T which is 13 cm away from the circle. What is the length (in cm) of AB?A103cmB203cmC403cmD163cm
Draw a circle of radius 3 cm. From a point 5 cm from the centre of the circle, draw two tangents to the circle. Measure the length of each tangent.
View SolutionIn a circle of radius 7 cm, tangent PT is drawn from a point P such that PT=24 cm.If O is the center of circle then length OP=?
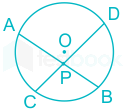
View SolutionIn the given figure, O is the centre of the circle. Its two chords AB and CD intersect each other at the point p within the circle. If AB=15cm,PB=9cm, then find the length of PD.
View SolutionO is the centre of the circle. OP = 5 and OT = 4, and AB = 8. The line PT is a tangent to the circle. Find PB

View SolutionO is the centre of a circle of radius 8 cm. The tangent at a point A on the circle cuts a line through O at B such that AB=15cm . Find OB .
View Solution
