Question

The line segments joining the midpoints M and N of parallel sides AB and DC respectively of a trapezium ABCD is perpendicular to both the sides AB and DC. Prove that AD=BC

Explanation

Given in trapazium ABCD ,Point M and N are the mid- point of parallel sides AB and DC respectively and join MN which is Pependiculaer to AB and DC.
To Prove AD=BC
Proof since ,M is the mid-poin of AB `therefore AM=MB `
Now,in `DeltaAMN and Delta BMN`
AM = MB [prove above ]
`angle 3=angle 4 [each 90^(@)`]
MN=MN [common side]
`therefore Delta AMN cong BMN` [by SAS congruence rule ]
`therefore angle 1 =angle 2` [by CPCT ]
On multiplying both sides of above equaltion by -1 and than adding `90^(@)` both sids ,we get
`90^(@)-angle 1=90^(@)-anlge 2`
`rArr angle AND= angle BNC`

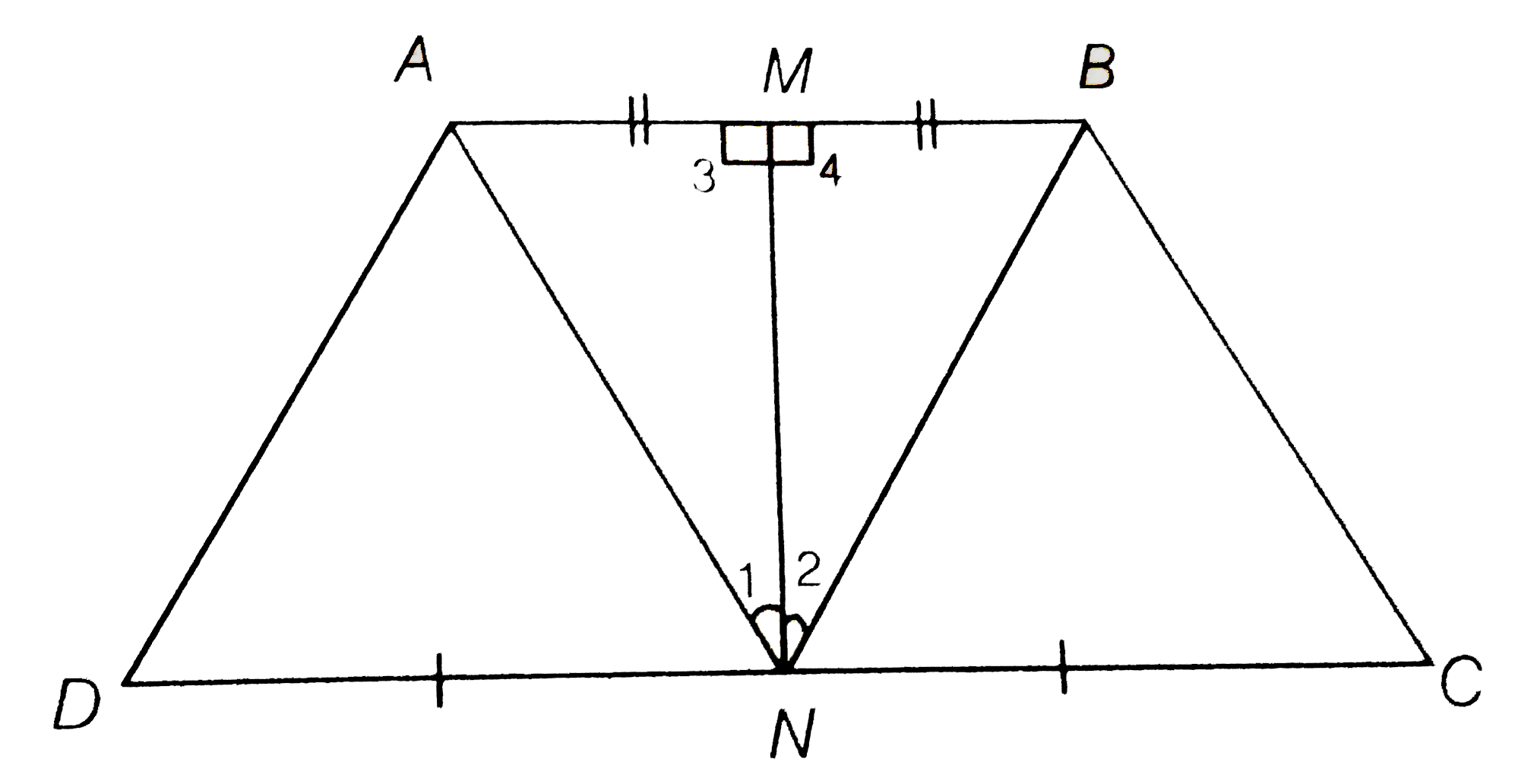
Now in `Delta ADN and Delta BCN `
`angle AND =angle BNC ` [from Eq.(i)]
AN=BN [`because Delta AMN cong Delta BMN`]
and DN=NC [`because` N is the mid-point of CD (given )]
`therefore Delta ADN cong Delta BCN ` [by SAS congruence rule ]
Hence AD= BC [by CPCT]