If ABCD is a quadilateral such that AB= AD and CB = CD ,then prove that AC is the perpendicular bisector of BD
Given In quadrilateral ABCD ,AB=AD and CB =CD
Construction join AC and BD
To prove AC in the perpendicular bisector of BD
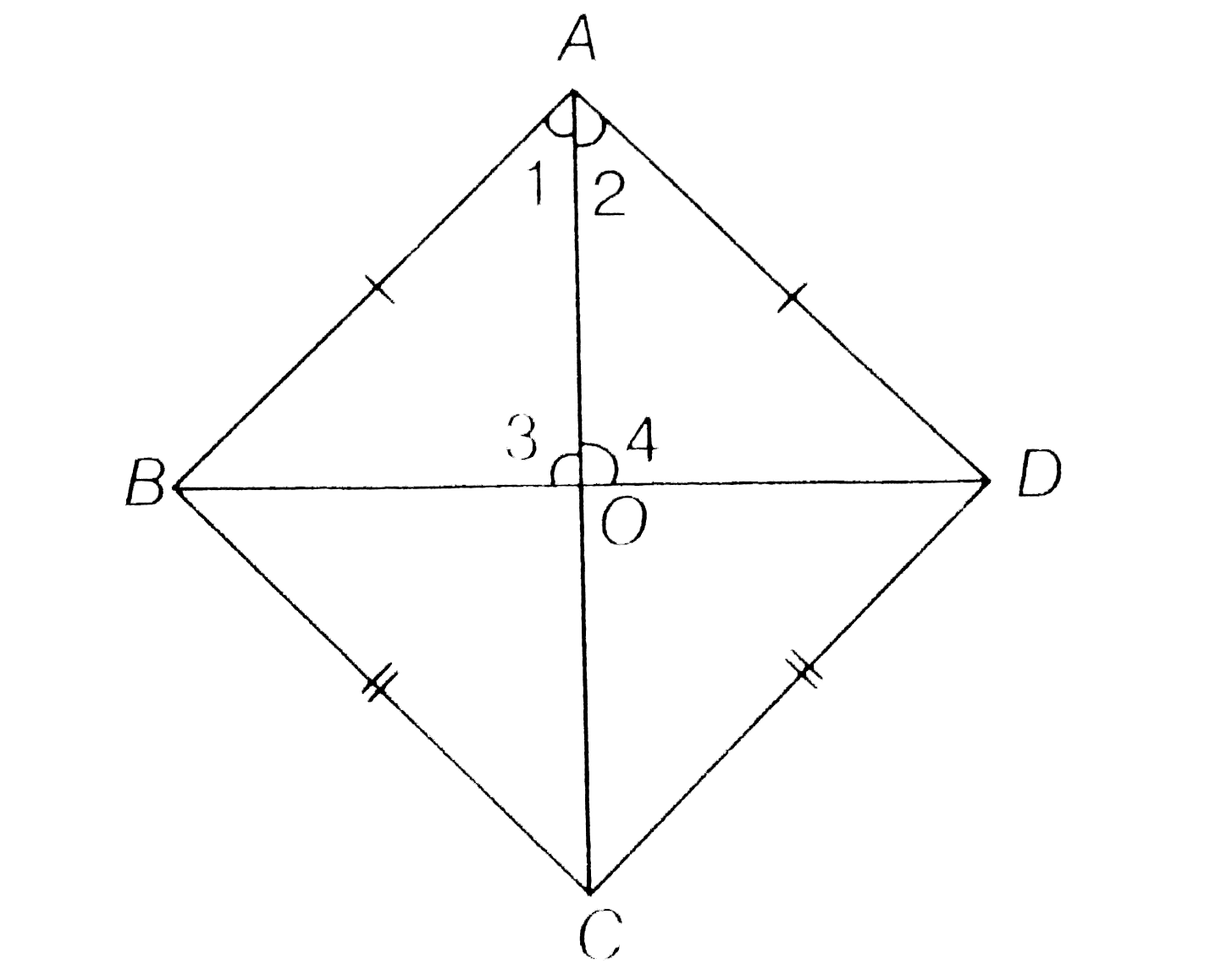
Proof In ΔABCandΔADC
AB=AD [given ]
BC =CD [given]
and AC =AC [common side ]
∴ΔABC≅ΔADC [by SSS congruence rule ]
⇒∠1=∠2 [by CPCT ]
Now in ΔAOBandΔAOD AB= AD [given ]
⇒∠1=∠2 [ proved above ]
and AO=AO [common side]
∴ΔAOB≅ΔAOD [by SAS congruence rule ]
→BO=DO [by CPCT]
and ∠3=∠4 [by CPCT ...(i)]
But ∠3+∠4=180∘ [linear pair axiom ]
⇒∠3+∠3=180∘ [from Eq. ...(i)]
⇒2∠3=180∘
⇒∠3=180∘2
∴∠3=90∘
Ac is perpendicular bisector of BD .
Topper's Solved these Questions
Similar Questions
In a quadrilateral ABCD, AB= AD and CB = CD, prove that AC is perpendicular bisector of BD.
View SolutionIf ABCD is a quadrilateral in which ABCD and AD=BC, prove that ∠A =∠B.
View SolutionIn the given figure, quadrilateral ABCD is a quadrilateral in which AB = AD and BC = DC. Prove that (i) AC bisects ∠A and ∠B, (ii) AC.is the perpendicular bisector of BD.
View SolutionABCD is a quadrilateral. Is AB+BC+CD+DA>AC+BD?
View SolutionIn Figure, if AB=AC and BE=CD, prove that AD=AE.
 View Solution
View SolutionIn a quadrilateral ABCD, it is given that AB∣∣CD and the diagonals ACandBD are perpendicular to each other. Show that AD.BC≥AB.CD.
View SolutionIn the given figure of AD = CB then prove that AC = BD
 View Solution
View SolutionThe midpoints of the sides AB,BC,CDandDA of a quadrilateral ABCD are joined to form a quadrilateral. If AC=BDandAC⊥BD then prove that the quadrilateral formed is a square.
View SolutionABCD is quadrilateral. Is AB+BC+CD+DA<2(AC+BD)?
View SolutionABCD is a quadri,aterial prove that (AB+BC+CD+DA)>(AC+BD)
 View Solution
View Solution

