In Figure, aAD and BE are respectively altitudes of an isosceles triangle ABC with AC=BC. Prove that AE=BD
Given ΔABC is an isosceles triangle in which AC=BC,AD and BE are respectively two altitude to sides BC and AC respectively
To Prove AE=BD
Proof in ΔABC AC=BC [given ]
∠ABC=∠CAB
[angles opposite to equal sides are equal ]
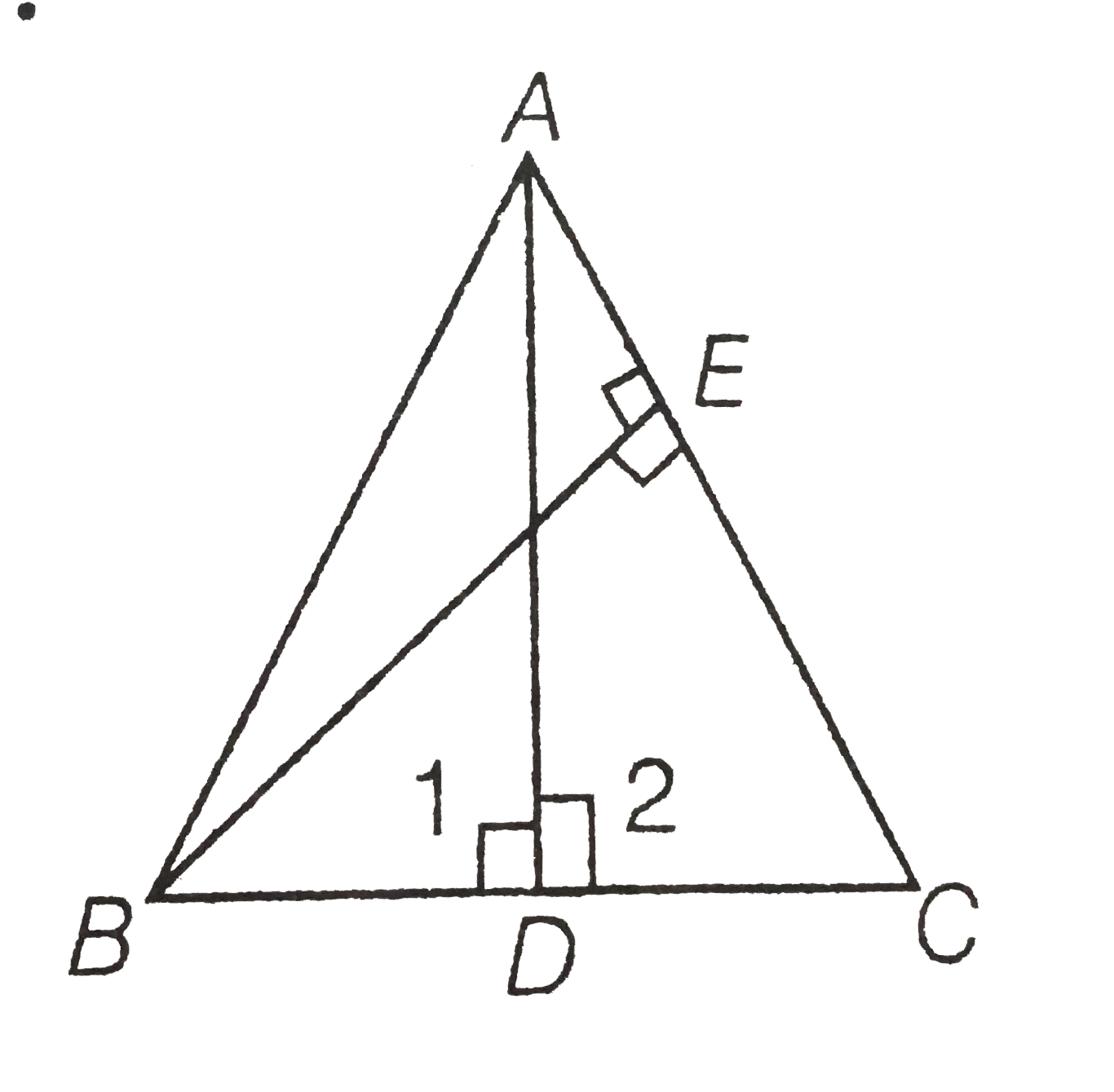
∠ABD=∠EAB
in ΔAEBandΔBDA,
∠AEB=∠ADB=90∘[ given ,AD⊥BC and BE⊥AC]
∠EAB=∠ABD [ from E q,(i) ]
and AB=AB [common side ]
∴ΔAEB≅ΔBDA [by AAS congruence rule ]
⇒ AE=BD [by CPCT ]
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
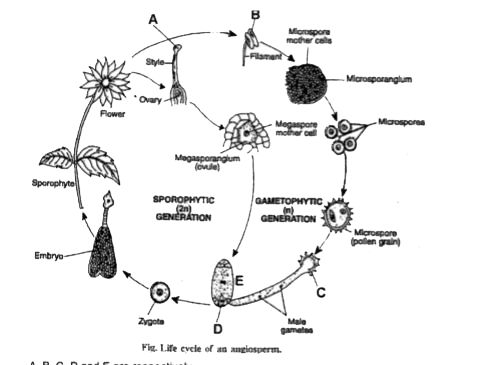
A, B, C, D and E are respectively -AStigma, Anther, Male gametophyte, Egg and Female gametophyteBStigma, Anther, Female gametophyte, Egg and Male gametophyteCStigma, Anther, Male gametophyte, Fertilized egg and Female gametophyteDStigma, Anther, Embryo sac, Egg and Female gametophyte
In a ABC,EandF are the mid-points of ACandAB respectively. The altitude AP to BC intersects FE at Q Prove that AQ=QP
View SolutionIn figure E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD⊥BCandEF⊥AC, prove thatΔABD~ΔECF.
 View Solution
View SolutionIn Fig. 4.124, E is a point on side CB produced of an isosceles triangle ABC with AB=AC . If AD⊥BC and EF⊥AC , prove that (i) ABDECF (ii) AB×EF=AD×EC . (FIGURE)
View SolutionIn Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD
 View Solution
View SolutionD and E are, respectively, the points on equal sides AB and AC of an isosceles triangle ABC such that B, C, E, and D are concyclic as shown in Figure. If O is the point of intersection of CD and BE, prove that AO is the bisector of line segment DE
View SolutionIn Figure, AD and BE are medians of ABC and BE∣∣DF . Prove that CF=14AC
Consider △ABC Since AD is Median
⇒BD=BC⋯(1)
Since BE is Median⇒AE=EC⋯(2)
Consider △BECSince BE∣∣DF
By Basic Proportionality theorm, ⇒BDDC=EFFC
From (1)⇒CF=EF
⇒CF=12AE
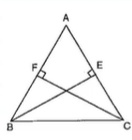
From (2)⇒CF=14ACView SolutionIn Figure, BD and CE are two altitudes of a ABC such that BD=CE. Prove that ABC is isosceles.
 View Solution
View Solution

