If the volume charge density of a dielectric sphere with a cavity (as shown in the figure) is ρ. Find the electrostatic self energy.

Self energy is equal to interaction energy of charges constituting the thick spherical shell.
Consider core of outer radius r having charge q, layer of infinitesimal thickness dr with charge dq.
Since core can be assumed to be a point charge at the centre wtih q=p.43π(r3−R3)
∴ Electrostatic interaction energy of point charge and the layer is given by
dU=14πε0q.dqr=14πε0=ρ43π(r3−R3).ρ4πr2drr
U=2R∫Rρ24π3ε0(r4−R3r)dr
U=ρ24π3ε0[r55−R3r22]2RR=9415ρ2πR5ε0

Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - SOLVED PROBLEMS (OBJECTIVE)15videos
ELECTROSTANTICS
- BOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - EXERCISE10videos
ELECTROSTANTICS
- BOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - MATRIX MATCH TYPE1videos
ELECTROSTANTICS
- BOOK - FIITJEECHAPTER - ELECTROMAGNETIC WAVE & WAVE OPTICSEXERCISE - ASSIGNMENT PROBLEMS Objective : Level-II (MULTI CHOICE SINGLE CORRECT)21videos
ELECTROMAGNETIC WAVE & WAVE OPTICS
- BOOK - FIITJEECHAPTER - ELECTROSTATICSEXERCISE - Example14videos
ELECTROSTATICS
Similar Questions
Knowledge Check
- Question 1 - Select One
A solid non-conducting sphere of radius R is charged with a uniform volume charge density ρ. Inside the sphere a cavity of radius r is made as shown in the figure. The distance between the centres of the sphere and the cavity is a. An electron of charge 'e' and mass 'm' is kept at point P inside the cavity at angle θ=45∘ as shown. If at t = 0 this electron is released from point P, calculate the time it will take to touch the sphere on inner wall of cavity again.
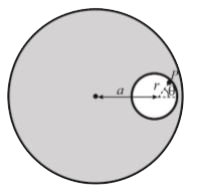 A√3Rmε0reρaB√6mε0reρaC√6√3mε0ReρaD√6√2mε0reρa
A√3Rmε0reρaB√6mε0reρaC√6√3mε0ReρaD√6√2mε0reρa
A solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.
 View Solution
View SolutionA solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.
 View Solution
View SolutionA Uniformly charged solid non-conducting sphere of uniform volume charge density ρ and radius R is having a concentric spherical cavity of radius r. Find out electric field intensity at following points, as shown in the figure :

(i) Point A (ii) Point B
(iii) Point C (iv) Centre of the sphereView SolutionA Uniformly charged solid non-conducting sphere of uniform volume charge density ρ and radius R is having a concentric spherical cavity of radius r. Find out electric field intensity at following points, as shown in the figure :

(i) Point A (ii) Point B
(iii) Point C (iv) Centre of the sphereView SolutionPositive charge is uniformly distrubuted with volume charge density ρ of sphere of radius R. A spherical cavity is created in the sphere as shown in figure. This electric field intensity inside the cavity at point P is(where CP =R/5 , C0C = 2R/3 , radius of cavity is R/4, C0 & C are centre of sphere & cavity respectively)
View SolutionA thick shell with inner radius R and outer radius 3R has a uniform charge density rho.It has a spherical cavity of radius R as shown in figure.The electric field at the centre of the cavity is nρR12ɛ0. Find n.
View SolutionA spherical cavity of radius r is made in a conducting sphere of radius 2 r.A charge q is kept at the centre of cavity as shown in the figure.Find the magnitude of the total electric field at (4r 0) .
View Solution

