Two concentric shells of radii d and 2d respectively are placed far away from a parallel plate capacitor. Each plate of the capacitor is a square of side d and the separation between the plates is d/4π. The charge on the plates are q and -q. Then the keys K1andK2 are closed, find the charges on the shells and electric potential left in the parallel plate capacitor in equilibrium.

Let the new charge on the parallel plate capacitor be +q1 and that on the concentric shells be (q−q1), such that the potential differences across the shells would be same as the potential difference across the plates.
ϕinnershell=(q−q1)4πε0(2d)+−(q−q1)4πε0d=−(q−q1)4πε0(2d)
ϕoutershell=q−q14πε0(2d)+−(q−q1)4πε0(2d)=0
Potential difference, Vshells=ϕouter−ϕinner=(q−q1)4πε0(2d)
For parallel plate, Vplates=q14πε0d
Vshells=Vplates
(q−q1)4πε0(2d)=q14πε0d
⇒(q−q1)=2q1
q1=q/3
∴ Charge on the outer shell = (q−q1)=23q
Charge on the inner shell = −2q/3
Energy left in the parallel plate capacitor = 12q21C=q272πε0d

Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - SOLVED PROBLEMS (OBJECTIVE)15videos
ELECTROSTANTICS
- BOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - EXERCISE10videos
ELECTROSTANTICS
- BOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - MATRIX MATCH TYPE1videos
ELECTROSTANTICS
- BOOK - FIITJEECHAPTER - ELECTROMAGNETIC WAVE & WAVE OPTICSEXERCISE - ASSIGNMENT PROBLEMS Objective : Level-II (MULTI CHOICE SINGLE CORRECT)21videos
ELECTROMAGNETIC WAVE & WAVE OPTICS
- BOOK - FIITJEECHAPTER - ELECTROSTATICSEXERCISE - Example14videos
ELECTROSTATICS
Similar Questions
Imagine a light planet revolving around a very massive star in a circular orbit of radius r with direction T. On what power of r, will the square of time period depends if the gravitational force of attraction between the planet and the star is proportional to r−5/2 .
View SolutionA parallel plate capacitor having plate area A and separation between the plates d is charged to potential V.The energy stored in capacitor is ....???
View Solution
Knowledge Check
- Question 1 - Select One or More
In a parallel-plate capacitor of plate area A, plate separation d and charge Q the force of attraction between the plates is F.
AF∝Q2BF∝1ACF∝dDF∝1d - Question 2 - Select One
A air filled parallel plate capacitor having circular plates of diameter D is given a charge Q.The magnitude of the force acting between plates is
AQ22ε0BQ22πD2ε0CQ2πD2ε0D2Q2πε0D2 - Question 3 - Select One
A parallel plate capacitor has area of each plate A, the separation between the plates is d. It is charged to a potential V and then disconnected from the battery. The amount of work done in the filling the capacitor Completely with a dielectric constant k is.
A12ε0AV2d[1−1k2]B12V2ε0AkdC12V2ε0Ak2dD12ε0AV2d[1−1K]
A air filled parallel plate capacitor having circular plates of diameter D is given a charge Q.The magnitude of the force acting between plates is
View SolutionThe distance between the plates of a parallel plate capacitor is 'd'. The capacitance of the capacitor gets doubled when a metal plate of thicknessd2 is placed between the plates.
View SolutionIn a parallel plate capacitor of capacitor 1μF two plates are given charges 2μC and 4μC the potential difference between the plates of the capacitor is
_2019_CBT2_E01_002_Q01.png) View Solution
View SolutionIn a parallel plate capacitor of capacitor 1μF two plates are given charges 2μC and 4μC the potential difference between the plates of the capacitor is
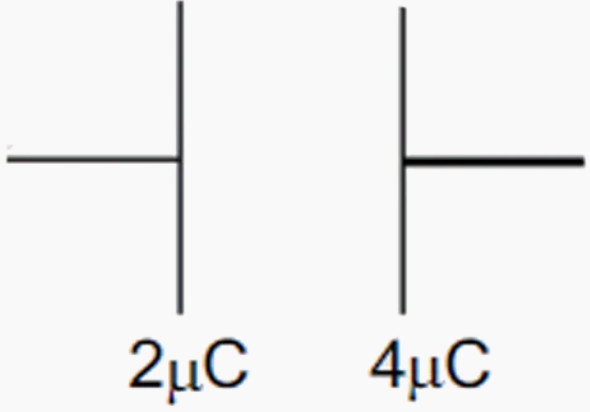 View Solution
View SolutionIn an isolated parallel plate capacitor of capacitance C, the plates have charge Q1 and Q2. The potential difference between the plates is
View Solution
