A ball of mass m with a charge q can rotate in a vertical plane at the end of a string of length l in a uniform electrostatic field whose lines of force are directed upwards. What horizontal velocity must be imparted to the ball in the upper position so that the tension in the string in the lower position of the ball is 1.5 times than the weight of the ball?
Gain in Kinetic Energy = Work done by external forces
implies gain in KE = Work done by gravity + work done by electrostatic force
⇒12m(v22−v21)=(mg)(2l)−(qE)(2l) ...(1)
For the ball at the lowermost position Q :
qE+T−mg=mv22l ...(2)
Putting T = Tension = 15 mg,
qE+15mg−mg=mv22l ...(3)
From (1) and (3) :
⇒12m(v22−v21)=2mgl−2qEl
⇒mv22−mv21=4mgl−4qEl
⇒mv22l=mv21l+4mg−4qE
Hence, 15mg+qE−mg=mv21l+4m−4qE
v1=√lm(10mg+5qE).

Topper's Solved these Questions
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - SOLVED PROBLEMS (OBJECTIVE)
15 Videos
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - EXERCISE
10 Videos
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - MATRIX MATCH TYPE
1 Videos
- ELECTROMAGNETIC WAVE & WAVE OPTICSBOOK - FIITJEECHAPTER - ELECTROMAGNETIC WAVE & WAVE OPTICSEXERCISE - ASSIGNMENT PROBLEMS Objective : Level-II (MULTI CHOICE SINGLE CORRECT)
21 Videos
- ELECTROSTATICSBOOK - FIITJEECHAPTER - ELECTROSTATICSEXERCISE - Example
14 Videos
Similar Questions
A light rod of length l is pivoted at the upper end. Two masses (each m), are attached to the rod, one at the middle and the other at the free end. What horizontal velocity must be imparted to the lower end mass, so that the rod may just take up the horizontal position ?
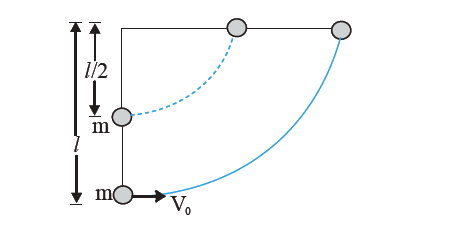
View SolutionA small ball of mass m having charge q is suspended by a string of length L. Another identical ball having the same charge is kept at the point of suspension. Determine the minimum horizontal velocity which should be imparted to ball at lowest point so that it can make complete revolution.
View Solution
Knowledge Check
A particle of mass m is suspended from a string of length l fixed to the point O. What velocity should be imparted to the particle in its lowermost position so that the string is just able to reach the horizontal diameter of the circle?
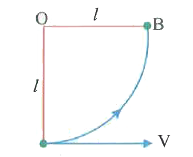 Av=√2glBv=√3glCv=√glDv=2gl
Av=√2glBv=√3glCv=√glDv=2glA particle of mass m and charge Q is attached to a string of length l. It is whirled in a vertical circle in the region of an electric field E as shown in the figure-5.105.What is the speed given to the particle at the point B,so that tension in the string when the particle is at A is ten times the weight of the particle?
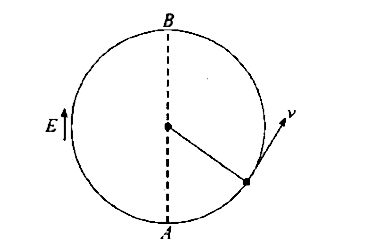 A√5glB√5(g−QEm)lC√QElmD√5(g+QEm)l
A√5glB√5(g−QEm)lC√QElmD√5(g+QEm)lA light rod of length l is pivoted at the upper end. Two masses (each m), are attached to the rod, one at the middle and the other at the free end. What horizontal velocity must be imparted to the lower end mass, so that the rod may just take up the horizontal position?
 A√6lg/5B√lg/5C√12lg/5D√2lg/5
A√6lg/5B√lg/5C√12lg/5D√2lg/5
A small ball having charge +q and mass m is suspended at one end of a light string of length and can rotate in vertical plane.A uniform electric field E exists in the region in vertically upward direction (mg>qE) .The minimum velocity required to be imparted to the ball at the lowest position in order to successfully negotiate the circular loop is √x(g−qEmy) then find x+y .x&y are lowest possible integer.
View Solutiona ball of mass 240g is attached to the verticle rod by means of two strings. When the ball rotates about the axis of rod, the strings are extended as shown in the figure.
(a) find the angular speed of the ball if tension in lower string is 16N.
(b) What is tension in the upper string?

View SolutionA body of mass m is tied to a string of length l and whirled in a verticle cirlce. The velocity of the body at the lowest position is u. Then the tension in the string at a position when the string makes an angle θ with the vertical is
View SolutionA body of mass m hangs at one end of a string of length l , the other end of which is fixed. It is given a horizontal velocity so that the string would just reach where it makes an angle of 60∘ with the vertical. The tension in the string at mean position is
View SolutionA ball of mass M is rotating in a conical pendulum by a string of length L. If radius of circular path is L√2, find the velocity of mass
View Solution
