Sketch the region {(x,0):y=√4−x2} and X-axis. Find the area of the region using integration.
The correct Answer is:N/a
Given region is {(x,0):y=√4−x2} and X-axis.
We have, y=√4−x2⇒y2=4−x2⇒x2+y2=4
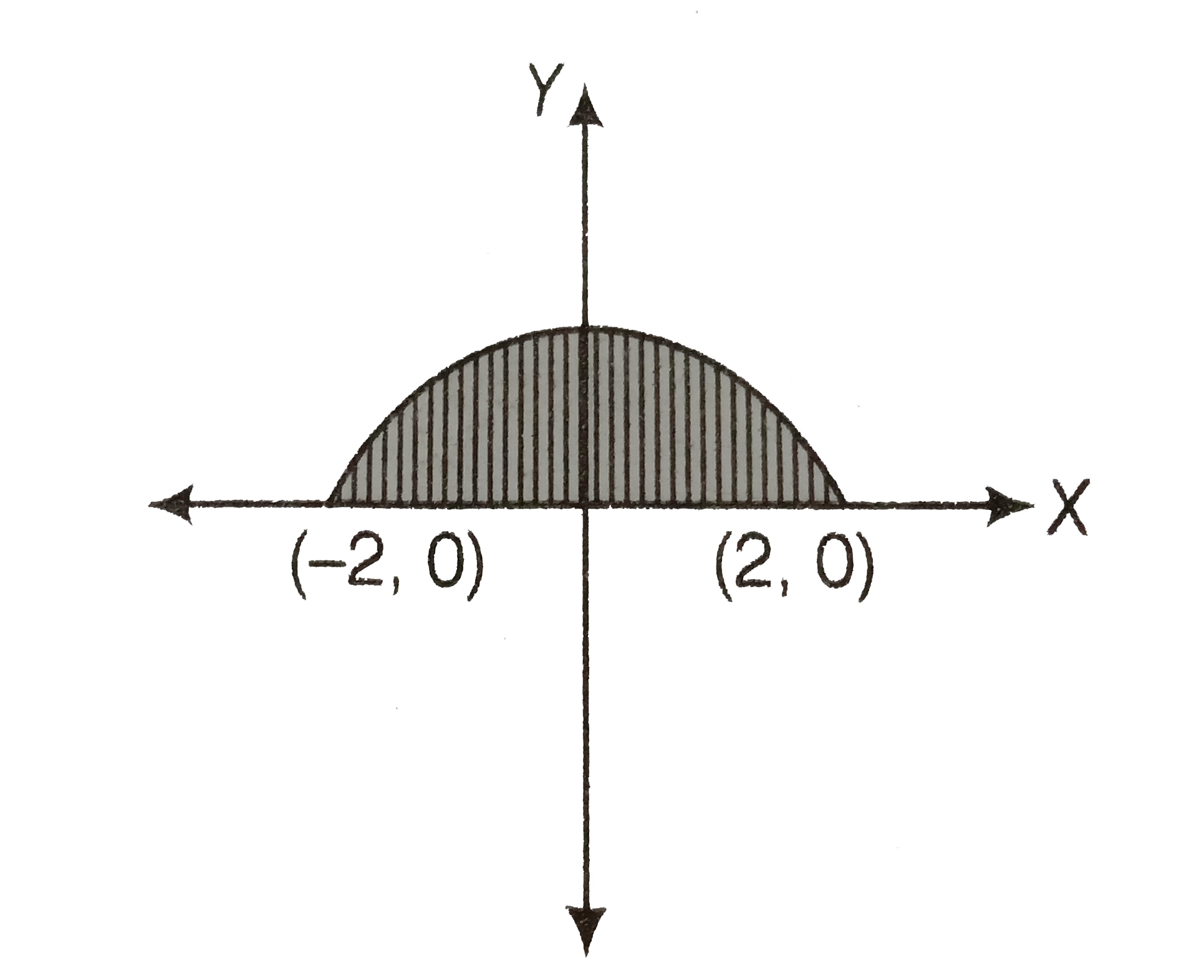
∴ Area of shaded region, A=∫2−2√4−x2dx=∫2−2√22−x2dx
=[x2√22−x2+222.sin−1(x)2]2−2
=22.0+0.π2+22.0−2sin−1(−1)=2.π2+2.π2
=2π sq units
Topper's Solved these Questions
Similar Questions
Sketch the region lying in the first quadrant and bounded by y=9x2,x=0,y=1andy=4. Find the area of the region using integration.
View SolutionSketch the region common to the cirvle x2+y2=25 and the parabola y2=8x Also find the area of the region using intergration .
View SolutionSketch the region common to the circle x2+y2=16 and the parabola x2=6y Also find the area of the region using intergration
View SolutionSketch the region lying in the first quadrant and bounded by y=4x2 ,x = 0, y = 2 and y = 4. Find the area of the region using integration.
View SolutionSketch the region {(x,y):4x2+9y2=36} and find its area, using integration.
View SolutionDraw a rough sketch of the following region and find the area enclosed by the region, using method of integration :
{(x,y):y2≤5x,5x2+5y2≤36}.View SolutionDraw a rough sketch of the region {(x,y):y2≤6 a x and x2+y2≤16a2}. Also, find the area of the region sketched using method of integration.
View SolutionSketch the region bounded by the curves y=√5−x2 and y=|x−1| and find its area.
View SolutionSketch the graph of y=√x+1in[0,4] and determine the area of the region enclosed by the curve, the axis of X and the lines x=0,x=4.
View SolutionDraw a rough sketch of the given curve y=1+|x+1|,x=−3,x≡3,y=0 and find the area of the region bounded by them, using integration.
View Solution

