Using integration, find the area of the region bounded by the line 2y=5x+7, X-axis and the line x=2 and x=8.
The correct Answer is:N/a
We have,22y=5x+7
⇒y=5x2+72
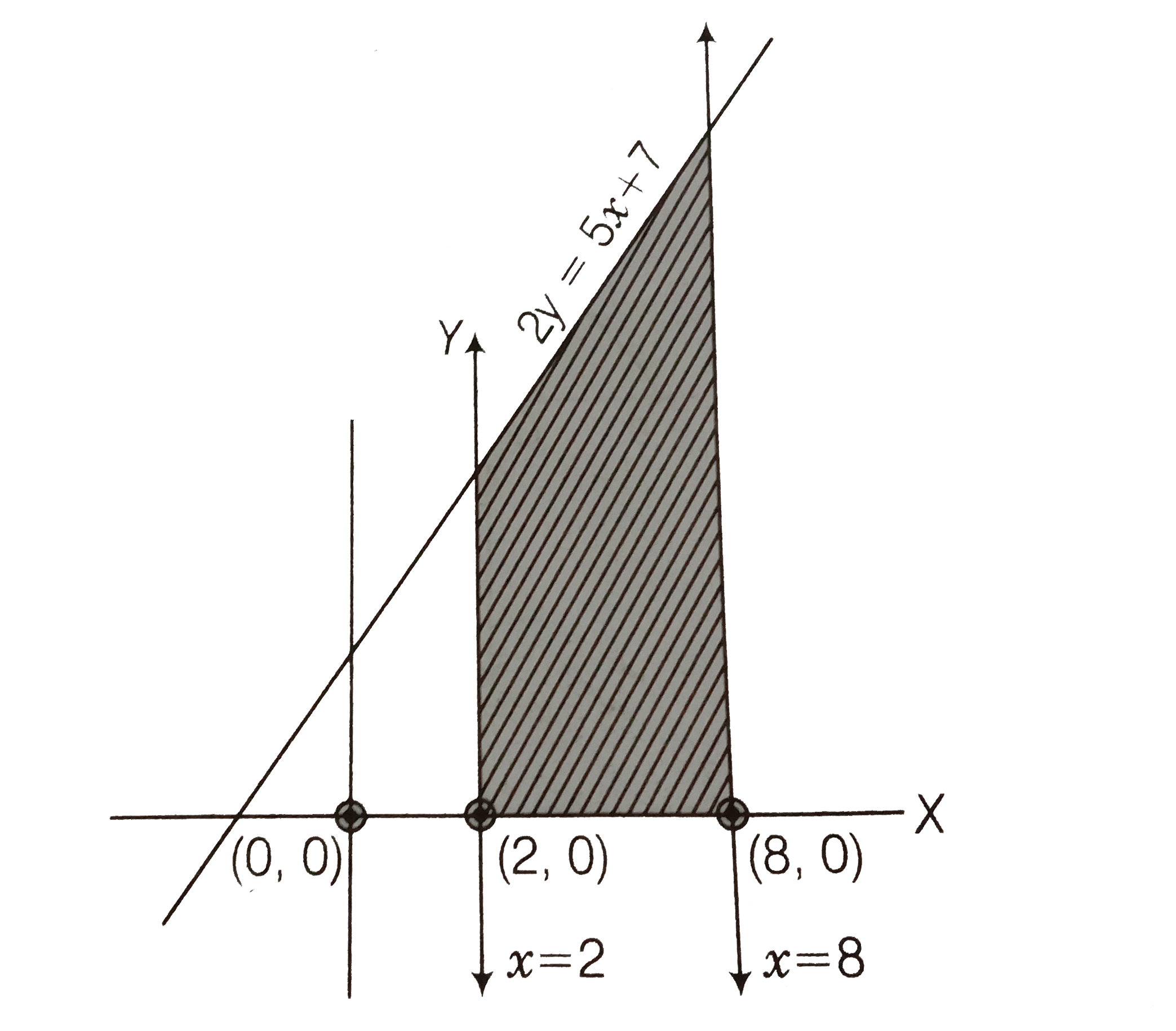
∴ Area of shaded region =12∫82(5x+7)dx=12[5.x22+7x]82
=12[5.32+7.8−10−14]12[160+56−24]
=1922=96 sq units
Topper's Solved these Questions
Similar Questions
Knowledge Check
Using integration, find the area of region bounded by the line 2x + y = 8, the y-axis and the lines y = 2 and y = 4.
A5 sq unitsB9 sq unitC6 sq unitsD2 sq units
Using integration, find the area of the region bounded by the line 2y=−x+8,x-axis is and the lines x=2 and x=4.
View SolutionUsing integration, find the area of the region bounded by the line 2y+x=8, the x-axis and the lines x=2 and x=4.
View SolutionUsing intergration find the area of the region bounded by the line 2y+x=8 x -axis and the lines x=2 and x = 4
View SolutionUsing integration, find the area of the region bounded by the line y-1 = x, the x-axis, and the ordinates x = -2 and x = 3.
View SolutionFind the area of the region bounded by the line y = 2x, X - axis and ordinate x = 2.
View SolutionUsing integration, find the area of the region bounded by the line y−1=x,thex−a xi s and the ordinates x=−2andx=3.
View SolutionFind the area of the region bounded by the curve4y=7x+9, the X-axis and the lines x=2andx=8.
View Solution
