Find the torque on M1 due to M2
Due to M2, magnetic fields at S and N of M1 are B1 and B2 respectively. The forces on −m and +m are F1 and F2 as shown in the figure.The torque (about the centre of the dipole m1) will be
F1a+F2a=(F1+F2)a
[(μ04π)M2(r−a)m+(μ04π)M2(r+a)m]a
(μ04π)M2m(1r3+1r3)a∵a<<r
μ0M2m4π2r3a=μ0M1M24π3

Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - PROBLEM
12 Videos
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-1 PART-1
81 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
Similar Questions
Knowledge Check
Two bodies of masses m1andm2 are separated by certain distance. If →F12 is the force on m1 due to m2 and →F21 is the force on m2 due to m1, then
AF12=F21B→F12=→F21C→F12=−→F21Dnone
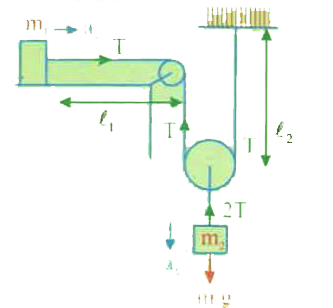
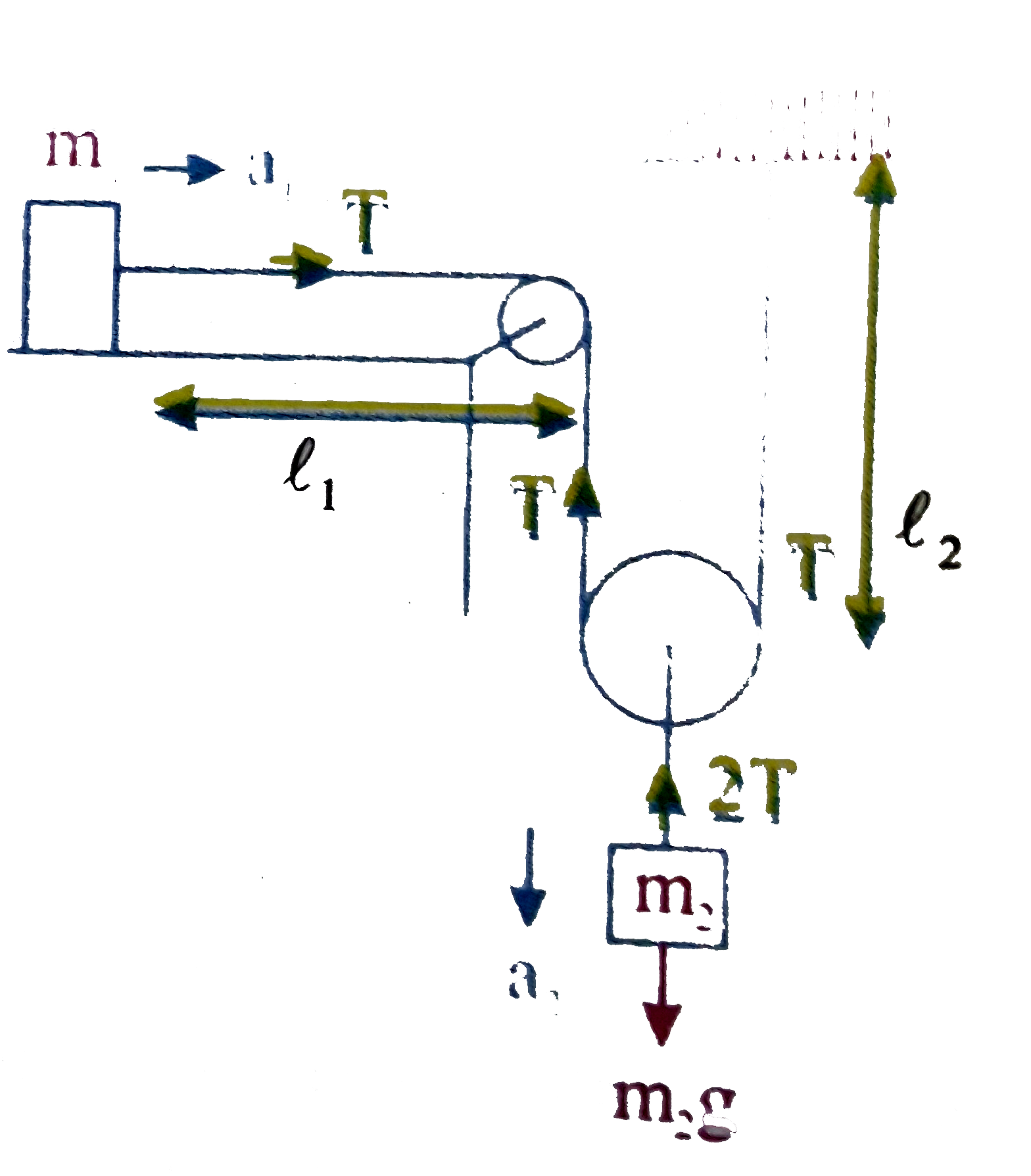
In the given diagram , find the relation between acceleration of blocks m1andm2 . (m2 remains horizontal ).
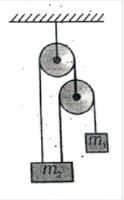
View SolutionIn the figure, m1 is at rest, find the relation among m1,m2 and m3 ? .
View SolutionA particle of mass m=1kg is projected with speed u=20√2m/s at angle θ=45∘ with horizontal find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle of mass m=1kg is projected with speed u=20√2m/s at angle θ=45∘ with horizontal find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionIf force →f=(3x→i+y2) W is acting on a body and body moves from (1m, 2m, 1m) to (2m, 3, 8m), then find the work done due to the force
View SolutionFind the magnetic force on a short magnet of magnetic dipole moment M2 due to another short magnet of magnetic dipole moment M1.
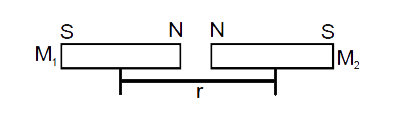
View SolutionFind the magnetic force on a short magnet of magnetic dipole moment M2 due to another short magnet of magnetic dipole moment M1.

View Solution

 .
.