A shell of relative density w.r.t water is just submerged in water. If its inner & outer radius is r and R then r/R is
The correct Answer is:A, B, C
To solve the problem, we need to find the ratio of the inner radius r to the outer radius R of a shell that is just submerged in water, given that its relative density with respect to water is 279.
1. Understanding Relative Density:
The relative density (specific gravity) is defined as the ratio of the density of a substance to the density of a reference substance (in this case, water).
Relative Density=Density of ShellDensity of Water=279=3
Therefore, the density of the shell (ρs) can be expressed as:
ρs=3⋅ρw
where ρw is the density of water.
2. Volume of the Shell:
The volume of the shell can be calculated using the formula for the volume of a hollow sphere:
V=43π(R3−r3)
3. Mass of the Shell:
The mass of the shell can be calculated using the density:
m=ρs⋅V=ρs⋅43π(R3−r3)
Substituting ρs:
m=3⋅ρw⋅43π(R3−r3)=4πρw(R3−r3)
4. Buoyant Force:
According to Archimedes' principle, the buoyant force (Fb) acting on the shell when it is submerged is equal to the weight of the water displaced by the shell:
Fb=ρw⋅Vdisplaced⋅g=ρw⋅43πR3⋅g
5. Equating Weight and Buoyant Force:
For the shell to be just submerged, the weight of the shell must equal the buoyant force:
4πρw(R3−r3)⋅g=ρw⋅43πR3⋅g
Canceling 4πg from both sides:
ρw(R3−r3)=13ρwR3
6. Simplifying the Equation:
Dividing both sides by ρw:
R3−r3=13R3
Rearranging gives:
R3−13R3=r3
23R3=r3
7. Finding the Ratio:
Taking the cube root of both sides:
r=R(23)1/3
Therefore, the ratio rR is:
rR=(23)1/3
Final Answer:
rR=(23)1/3
The relative density (specific gravity) is defined as the ratio of the density of a substance to the density of a reference substance (in this case, water).
Relative Density=Density of ShellDensity of Water=279=3
Therefore, the density of the shell (ρs) can be expressed as:
ρs=3⋅ρw
where ρw is the density of water.
The volume of the shell can be calculated using the formula for the volume of a hollow sphere:
V=43π(R3−r3)
The mass of the shell can be calculated using the density:
m=ρs⋅V=ρs⋅43π(R3−r3)
Substituting ρs:
m=3⋅ρw⋅43π(R3−r3)=4πρw(R3−r3)
According to Archimedes' principle, the buoyant force (Fb) acting on the shell when it is submerged is equal to the weight of the water displaced by the shell:
Fb=ρw⋅Vdisplaced⋅g=ρw⋅43πR3⋅g
For the shell to be just submerged, the weight of the shell must equal the buoyant force:
4πρw(R3−r3)⋅g=ρw⋅43πR3⋅g
Canceling 4πg from both sides:
ρw(R3−r3)=13ρwR3
Dividing both sides by ρw:
R3−r3=13R3
Rearranging gives:
R3−13R3=r3
23R3=r3
Taking the cube root of both sides:
r=R(23)1/3
Therefore, the ratio rR is:
rR=(23)1/3
rR=(23)1/3
Topper's Solved these Questions
Similar Questions
A sperical iron shell floats almost, completely submerged submerged in water . If its outer diameter is 0.5 m and the relative density of iron is 8 m find the inner diameter.
View SolutionWhat is the volume of the material in a spherical shell with inner radius ‘r' and outer radius 'R' ?
View Solution
Knowledge Check
- Question 1 - Select One
The relative density of SO2 gas w.r.t O2 gas is
A1B2C3D4 - Question 2 - Select One
A sphere of solid material of relative density 9 has a concentric spherical cavity and sinks in water. If te radius of the sphere be R. Then the radius of the cavity (r) will be related to R as
Ar3=89R3Br3=23R3Cr3=√83R3Dr3=√23R3 - Question 3 - Select One
A sperical ball of radius r and relative density 0.5 is floating in equilibrium in water with half of it immersed in water. The work done in pushing the ball down so that whole of it is just immersed in water is [ρ is the density of water]-
A0.25 ρrgB0.5 ρ rgC43πr3ρgD512πr4ρg
The lateral surface area of a hollow cylinder of outer radius R, inner radius r and height h is_______.
View SolutionA spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
(a) A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell ?View SolutionHeat flows radially outwards through a spherical shell of outside radius R2 and inner radius R1. The temperature of inner surface of shell is θ1 and that of outer is θ2. At what radial distance from centre of shell the temperature is just half way between θ1andθ2?
View Solution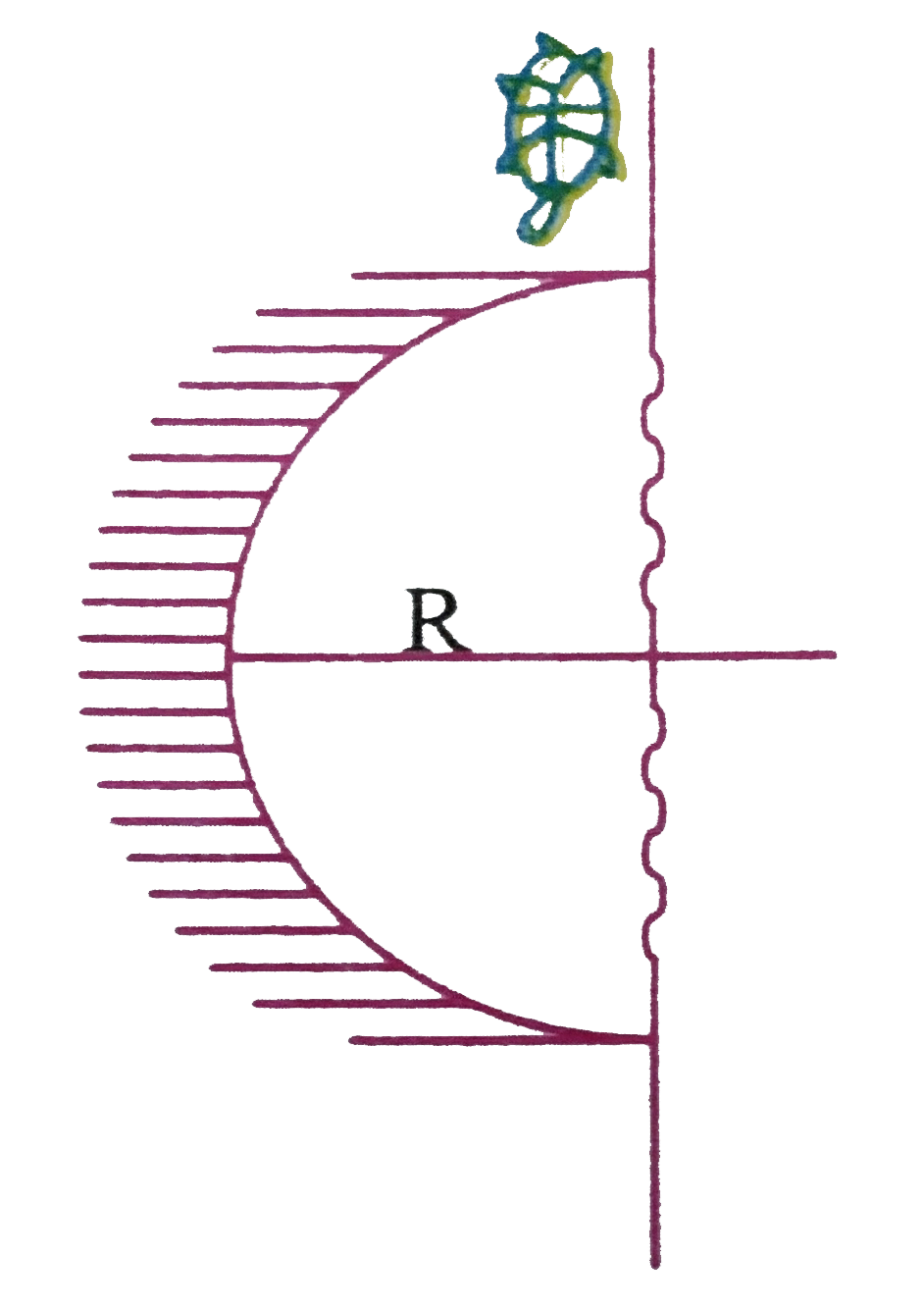
A tortoise is just sinking in water of density ρ The tortoise is assumed to be3 a hemisphere of radius R.
Find vertical thrustView SolutionConsider two concentric spherical metal shells of radii r1 and r2(r2>r1). If the outer shell has a charge q and the inner one is grounded, then the charge on the inner shell is
View Solution

