Radioactive nucleus A decays into B with half-life 10sec. A also convert into C with half-life 100sec. Find half-life of A for both emission.
6sec
9sec
3sec
2sec
The correct Answer is:B
To solve the problem of finding the half-life of radioactive nucleus A when it decays into both B and C, we can follow these steps:
1. Understand the Decay Process:
- Nucleus A decays into B with a half-life T(B)1/2=10 seconds.
- Nucleus A decays into C with a half-life T(C)1/2=100 seconds.
2. Define Decay Constants:
- The decay constant λ is related to the half-life by the formula:
λ=ln(2)T1/2
- For decay into B:
λ1=ln(2)10
- For decay into C:
λ2=ln(2)100
3. Combine Decay Constants:
- Since A decays into both B and C, the total decay constant λeq is the sum of the individual decay constants:
λeq=λ1+λ2
- Substituting the values:
λeq=ln(2)10+ln(2)100
4. Finding a Common Denominator:
- The common denominator for 10 and 100 is 100:
λeq=10ln(2)100+ln(2)100=11ln(2)100
5. Calculate the Equivalent Half-Life:
- Using the relationship between decay constant and half-life:
T(eq)1/2=ln(2)λeq=ln(2)11ln(2)100=10011
- Calculating 10011 gives approximately 9.09 seconds.
Final Answer:
The half-life of nucleus A for both emissions is approximately 9 seconds.
---
- Nucleus A decays into B with a half-life T(B)1/2=10 seconds.
- Nucleus A decays into C with a half-life T(C)1/2=100 seconds.
- The decay constant λ is related to the half-life by the formula:
λ=ln(2)T1/2
- For decay into B:
λ1=ln(2)10
- For decay into C:
λ2=ln(2)100
- Since A decays into both B and C, the total decay constant λeq is the sum of the individual decay constants:
λeq=λ1+λ2
- Substituting the values:
λeq=ln(2)10+ln(2)100
- The common denominator for 10 and 100 is 100:
λeq=10ln(2)100+ln(2)100=11ln(2)100
- Using the relationship between decay constant and half-life:
T(eq)1/2=ln(2)λeq=ln(2)11ln(2)100=10011
- Calculating 10011 gives approximately 9.09 seconds.
The half-life of nucleus A for both emissions is approximately 9 seconds.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A nucleus A (parent) decays into B (Daughter) with half life T1 and B decays into C with half life T2. Graph is drawn between number of atoms/activity versus time. Select the correct graph (s)
A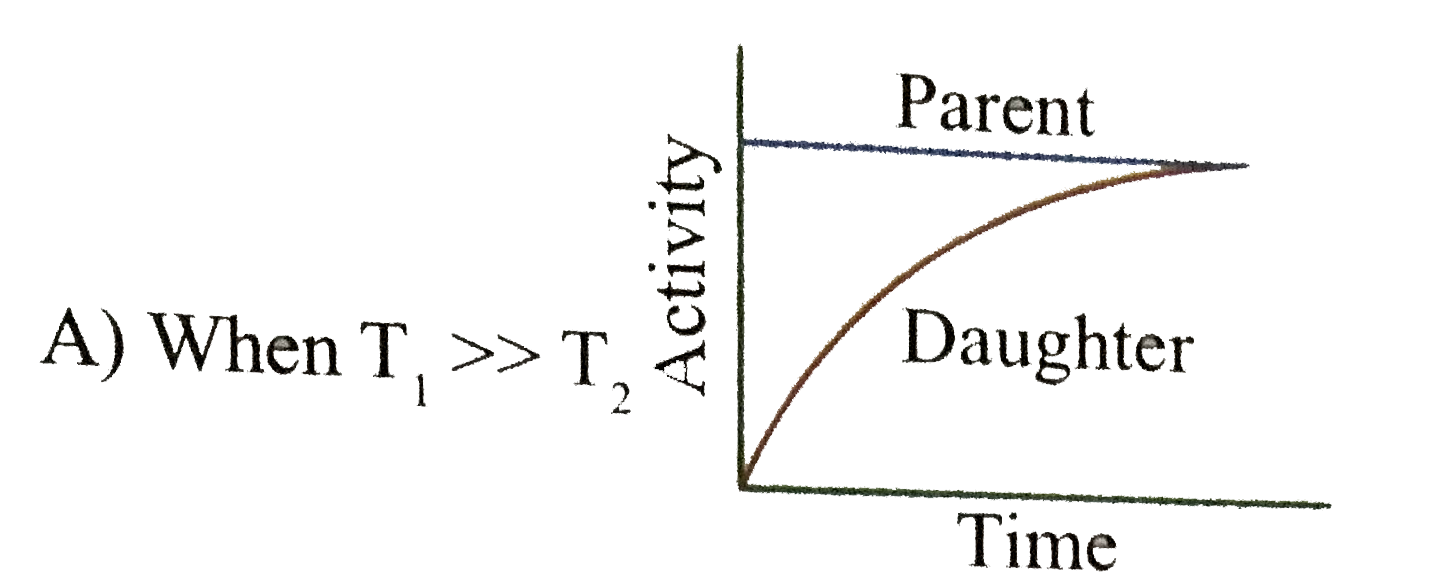 B
B C
C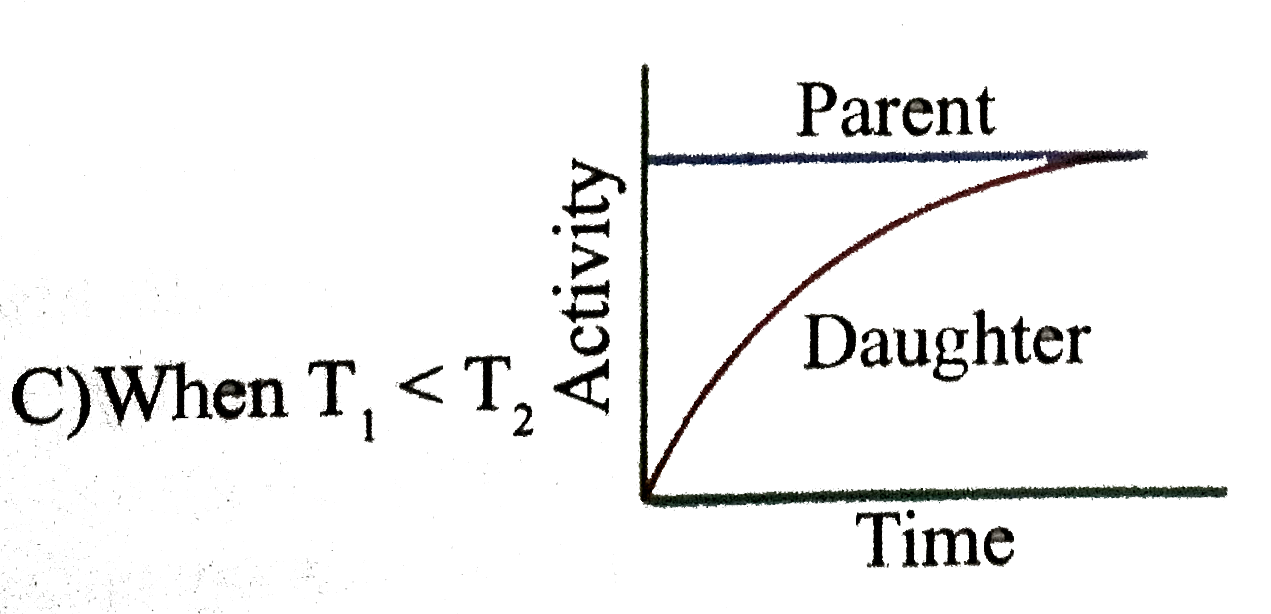 D
D
If the half-life of a radioactive sample is 10 hours its mean life is
A14.4 hB7.2 hC20 hD6.93 hHalf-life period for radioactive element is
AAlways constantBVariableCIndependent of final concentrationnDIndependent of initial concentration
A radioactive nucleus can decay by three different processes. Half life for first process is 2 hours . Effective half life of the necleus is 43 hours. Find the half for second process in hours.
View SolutionA radiocative nucleus deays by two different processes. The half life for the first process is 10 s and that for the second is 100 s. The effective half life of the nucleus is close to :
View SolutionThe decay constant of a radioactive substance is 0.693 per minute. What will be the half-life and mean life of it?
View SolutionA radioactive nucleus can decay by two different processes . The half life for the first process is t1 and that for the second process is t2. If effective half life is t, then
View SolutionThe fraction quantity of a radiactive sample will decay during half of its half-life period is
View Solution
