If a helicopter is moving upwards with acceleration g and food packet are thrown from a height h. Find time period to reach those packet to ground
The correct Answer is:A, B
To solve the problem of finding the time it takes for food packets thrown from a helicopter moving upwards with acceleration g to reach the ground from a height h, we can follow these steps:
Step 1: Determine the velocity of the helicopter at height h
The helicopter is moving upwards with an acceleration g. We can use the kinematic equation:
v2=u2+2as
Where:
- v is the final velocity,
- u is the initial velocity (0, since it starts from rest),
- a is the acceleration (g),
- s is the displacement (h).
Substituting the values:
v2=0+2gh
Thus, the final velocity v when the helicopter reaches height h is:
v=√2gh
Step 2: Analyze the motion of the food packet after it is released
When the food packet is released from the helicopter, it has an initial upward velocity u=√2gh and will be acted upon by gravity, which will decelerate it.
Step 3: Set up the equation of motion for the food packet
The food packet will first move upwards until its velocity becomes zero and then it will start falling down. We need to find the time it takes for the packet to reach the ground.
Using the kinematic equation for displacement:
s=ut+12at2
Where:
- s is the total displacement (which will be −h since it moves from height h to the ground),
- u=√2gh (initial velocity),
- a=−g (acceleration due to gravity acting downwards),
- t is the time taken.
Substituting the values:
−h=√2gh⋅t−12gt2
Step 4: Rearranging the equation
Rearranging gives us:
12gt2−√2gh⋅t−h=0
This is a quadratic equation in t of the form at2+bt+c=0, where:
- a=12g,
- b=−√2gh,
- c=−h.
Step 5: Solve the quadratic equation
Using the quadratic formula t=−b±√b2−4ac2a:
t=−(−√2gh)±√(−√2gh)2−4⋅12g⋅(−h)2⋅12g
This simplifies to:
t=√2gh±√2gh+2ghg
t=√2gh±√4ghg
t=√2gh±2√ghg
Step 6: Choose the appropriate solution
Since time cannot be negative, we take the positive root:
t=√2gh+2√ghg
Factoring out √gh:
t=√gh(√2+2)g
Final Result
Thus, the time taken for the food packets to reach the ground is:
t=(√2+2)√h√g
- v is the final velocity,
- u is the initial velocity (0, since it starts from rest),
- a is the acceleration (g),
- s is the displacement (h).
- s is the total displacement (which will be −h since it moves from height h to the ground),
- u=√2gh (initial velocity),
- a=−g (acceleration due to gravity acting downwards),
- t is the time taken.
- a=12g,
- b=−√2gh,
- c=−h.
Topper's Solved these Questions
Similar Questions
A helicopter rises from rest on the ground vertically upwards with a constant acceleration g. A food packet is dropped from the helicopter when is at a height h. The time taken by the packet to reach the ground is close to [ g is the acceeration due to gravity] :
View SolutionAn aeroplane is moving with a velocity u. It drops a packet from a height h. The time t taken by the packet in reaching the ground will be
View Solution
Knowledge Check
A balloon is going upwards with velocity 12m/sec it releases a packet when it is at a height of 65 m from the ground. How much time the packet will take to reach the ground (g=10m/sec2)
A5 secB6 secC7 secD8 secA packet is released from a balloon which is moving upward when the balloon is at a height 200 m above ground. The packet reaches the ground in 8 sec. Speed of the balloon when the packet is released, is: (Take g=10m/s2)
A18 m/sB15 m/sC12 m/sD9 m/sAn aeroplane moving horizontally with a speed of 180km/hr. drops a food packet while flying at a height of 490m. The horizontal range of the packet is:-
A180mB980mC500mD670m
A balloon starts rising upwards with constant acceleration a and afrer time t0, second, a packet is dropped from it which reaches the ground aftre t seconds of dropping . Derermine the value of t
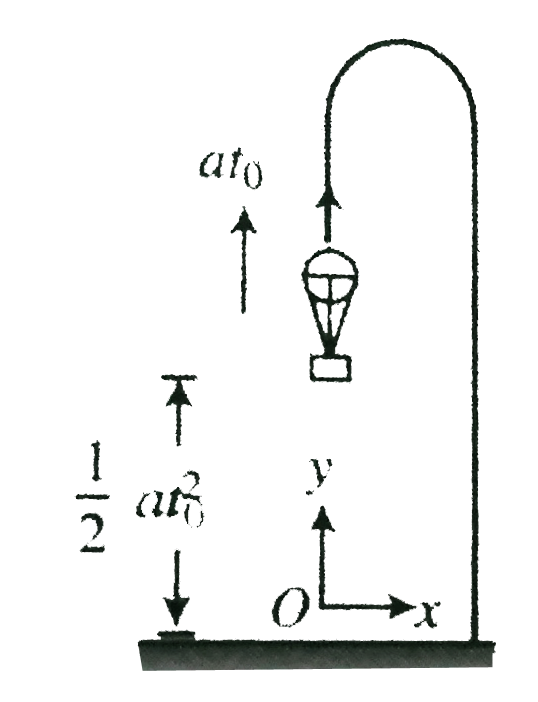 .
.
View SolutionA helicopter is moving verticallly upwards with a velocity 5ms−1. When the helicopter is at a height 10m from ground, a stone is thrown with a velocity (3ˆi+4ˆj)ms−1 from the helicopter w.r.t. the man in it. Considering the point on ground vertically below the helicopter as the origin of coordinates, and the ground below as xy plane, find the coordinates of the point where the stone will fall, its distance from origin at the instant the stone strikes the ground, assuming helicopter moves upwards with constant velocity.
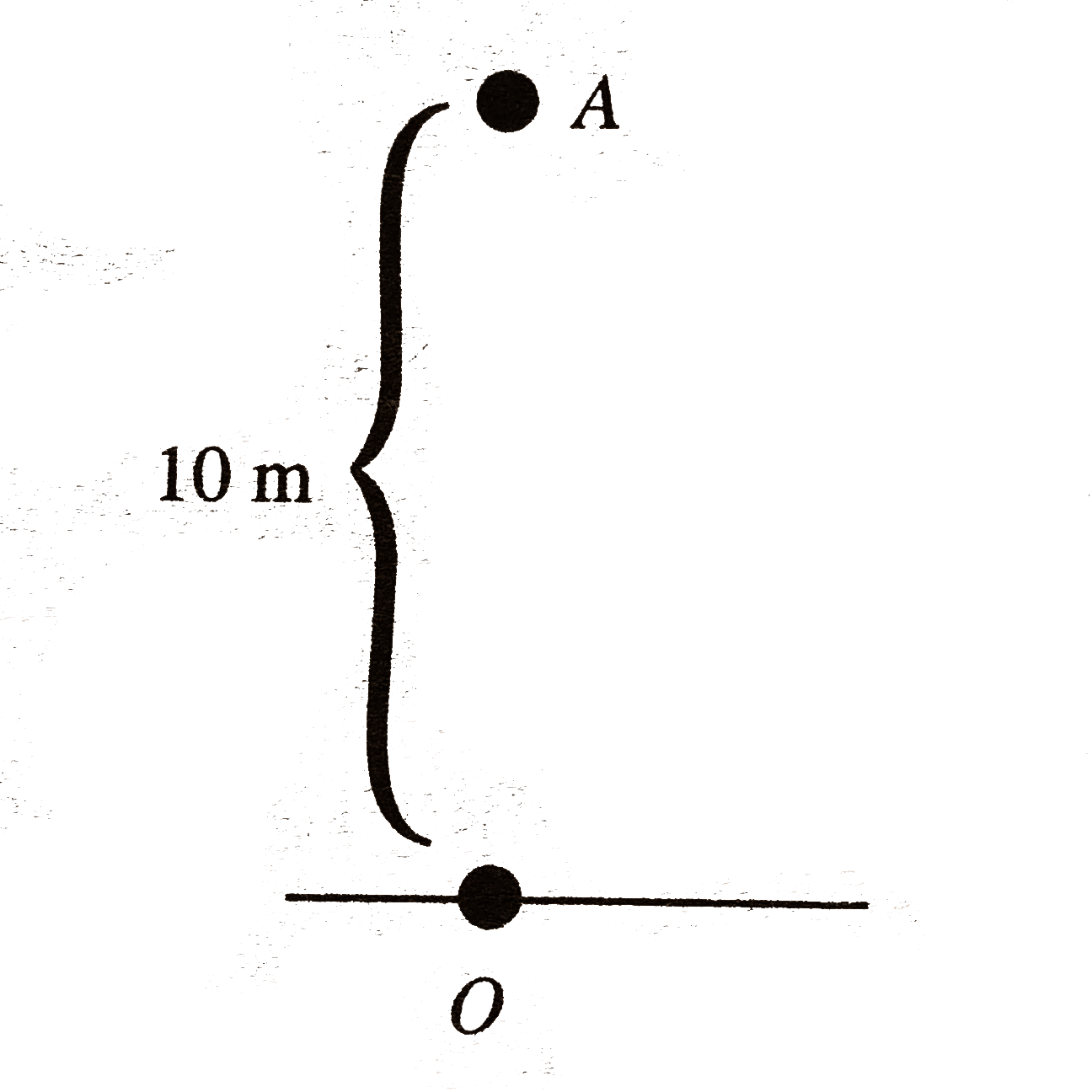 .
.
View SolutionA ball is thrown upwards with a speed u from a height h above the ground.The time taken by the ball to hit the ground is
View SolutionA stone thrown down with a seed u takes a time t1 to reach the ground , while another stone, thrown upwards from the same point with the same speed, takes time t2. The maximum height the second stone reaches from the ground is
View SolutionA helicopter, moving vertically upwards, releases a packet when it is a certain height the ground. The packet initially moves upwards for a time t1 and then falls dowanwards for a time t2 until it reaches the ground. Then
View Solution
