Given that x=(1√ε0μ0), y=EB & z=(1RC) . which of the following in correct.
dimension of x and z will be same
dimension of y and z will be same
dimension of x and y will be same
dimension of x,y and z is different
To solve the problem, we need to analyze the dimensions of the given quantities x, y, and z.
1. Identify the expressions for x, y, and z:
- x=1√ϵ0μ0
- y=EB
- z=1RC
2. Determine the dimension of x:
- The speed of light c is given by the relation c=1√ϵ0μ0.
- The dimension of speed c is (LT−1).
- Therefore, the dimension of x is also (LT−1).
3. Determine the dimension of y:
- The ratio y=EB where E is the electric field and B is the magnetic field.
- The electric field E has the dimension (MLT−3A−1) and the magnetic field B has the dimension (MT−2A−1).
- Thus, the dimension of y can be calculated as:
(y)=(E)(B)=(MLT−3A−1)(MT−2A−1)=(LT−1)
- Therefore, the dimension of y is also (LT−1).
4. Determine the dimension of z:
- The expression z=1RC where R is resistance and C is capacitance.
- The dimension of resistance R is (ML2T−3A−2) and the dimension of capacitance C is (M−1L−2T4A2).
- Thus, the dimension of z can be calculated as:
(z)=1(R)(C)=1(ML2T−3A−2)(M−1L−2T4A2)
- Simplifying this gives:
(z)=(T−1)
5. Compare the dimensions:
- From the calculations:
- (x)=(LT−1)
- (y)=(LT−1)
- (z)=(T−1)
- We see that x and y have the same dimensions, while z has a different dimension.
6. Conclusion:
- The correct statement is that x and y have the same dimensions, while z has a different dimension.
Final Answer:
The correct option is that the dimensions of x and y are the same.
- x=1√ϵ0μ0
- y=EB
- z=1RC
- The speed of light c is given by the relation c=1√ϵ0μ0.
- The dimension of speed c is (LT−1).
- Therefore, the dimension of x is also (LT−1).
- The ratio y=EB where E is the electric field and B is the magnetic field.
- The electric field E has the dimension (MLT−3A−1) and the magnetic field B has the dimension (MT−2A−1).
- Thus, the dimension of y can be calculated as:
(y)=(E)(B)=(MLT−3A−1)(MT−2A−1)=(LT−1)
- Therefore, the dimension of y is also (LT−1).
- The expression z=1RC where R is resistance and C is capacitance.
- The dimension of resistance R is (ML2T−3A−2) and the dimension of capacitance C is (M−1L−2T4A2).
- Thus, the dimension of z can be calculated as:
(z)=1(R)(C)=1(ML2T−3A−2)(M−1L−2T4A2)
- Simplifying this gives:
(z)=(T−1)
- From the calculations:
- (x)=(LT−1)
- (y)=(LT−1)
- (z)=(T−1)
- We see that x and y have the same dimensions, while z has a different dimension.
- The correct statement is that x and y have the same dimensions, while z has a different dimension.
The correct option is that the dimensions of x and y are the same.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A conducting sphere A of radius a, with charge Q, is placed concentrically inside a conducting shell B of radius b. B is earthed. C is the common center of AandB. Study the following statements.
(i) The potential at a distance r from C, where
a≤r≤b,is14πε0(qr)
(ii) The potential difference between AandB is
14πε0Q(1r−1B)
(iii) The potential at a distance r from C, where
a≤r≤b,is14πε0Q(1r−1B)
Which of the above statements are correct ?
 .AOnly (i) and (ii)BOnly (ii) and (iii)COnly (i) and (iii)DAll of these
.AOnly (i) and (ii)BOnly (ii) and (iii)COnly (i) and (iii)DAll of theseGiven the equation of the line 3x−y+z+1=0and5x−y+3z=0. Then,which of the following is correct?
ASymmetrical form of the equation of line is x2=y−18−1=z+581.BSymmetrical form of the equation of line is x+181=y−58−1=z−2CEquation of the through (2,1,4) and perpencular to the given lines is 2x−y+z−7=0.DEquation of the plane through (2,1,4) and perpendicular to the given lines is x+y−2z+5=0.For the function f(x)=e1x−1e1/x+1,x=0 , which of the following is correct .
Alimx→0f(x) does not existBlimx→0f(x)=1Climx→0f(x) exist but f(x) is not continuous at x =0Df(x) is continuous at x =0
The dimension of 1√ε0μ0 is that of
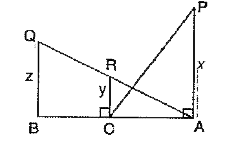
View SolutionIn the given figure, if PA = x, RC = y and QB = z, then which one of the following is correct?
View SolutionSuppose the system of equations
a1x+b1y+c1z=d1
a2x+b2y+c2z=d2
a3x+b3y+c3z=d3
has a unique solution (x0,y0,z0). If x0=0, then which one of the following is correct ?
View SolutionFor the function
f(x) = f(x)={((e^(1//x)-1)//(e^(1//x)+1),xne0),(0,x=0):} x=0, which of the following is correct :
View SolutionFor the function
f(x) = f(x)={((e^(1//x)-1)//(e^(1//x)+1),xne0),(0,x=0):} x=0, which of the following is correct :
View Solution
