Let $f (x) = x sin π x, x > 0$ . Then for all natural numbers $n, f^{'} (x)$ vanishes at A unique point in the interval $(n, n + \frac{1}{2})$ a unique point in the interval $(n + \frac{1}{2}, n + 1)$ a unique point in the interval $(n, n + 1)$ two points in the interval $(n, n + 1)$

Video Solution

Text Solution

Verified by Experts

We have $f' (x) = sin π x + π x cos π x = 0$
$\Rightarrow tan π x = - π x$
Now we draw the graphs of $y = tan π x$ and $y = - π x$ and look for their points of intersection. $y = tan π x$ has period 1.
Graphs are as shown in the following figure.

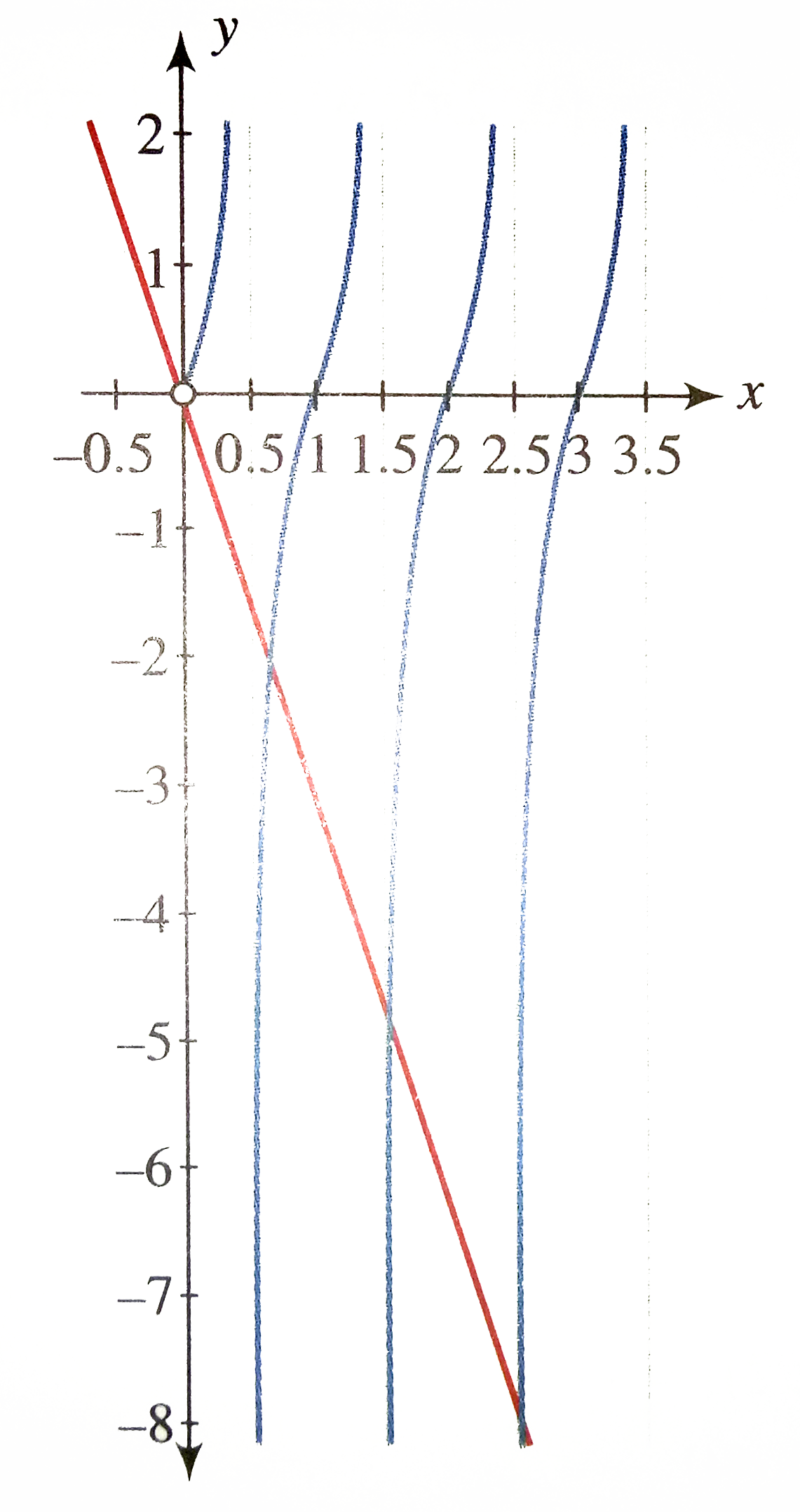
$\Rightarrow x \in (n + \frac{1}{2}, n + 1) or (n, n + 1)$
Hence (b) and (c) are correct options.

|

Updated on:21/07/2023

Class 12 MATHS GRAPHS OF TRIGONOMETRIC FUNCTIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Let $x_{n} = {(2^{n} + 3^{n})}^{1 / 2 n}$ for all natural number n.
Then
A $lim n \to \infty x_{n} = \infty$
B $lim n \to \infty x_{n} = \sqrt{3}$
C $lim n \to \infty x_{n} = \sqrt{3} + \sqrt{2}$
D $lim n \to \infty x_{n} = \sqrt{5}$
Question 2 - Select One
Suppose the function $f (x) = x^{n}, n \neq 0$ is differentiable for all x. then n can be any element of the interval
A $[1, \infty)$
B $(0, \infty)$
C $(1 / 2, \infty)$
Dnone of the above
Question 3 - Select One
Let n be a natural and let 'a' be a real number. The number of zeros of $x^{2 n + 1} - (2 n + 1) x + a = 0$ in the interval $[- 1, 1]$ is -
A2 if a gt 0
B2 if a lt 0
CAt most one for every value of a
DAt least three for every value of a

CENGAGE-GRAPHS OF TRIGONOMETRIC FUNCTIONS-Exercise

Home
Ask Doubt
Profile