Solve sinθ+√3cosθ≥1,−π<θ≤π.
Video Solution
Text Solution
The given inequation is
sinθ+√3cosθ≥1,−π<θ≤π
⇒ 12sinθ+(√3/2)cosθ≥12
⇒ cos(θ−π6)≥12
⇒ cosx≥12, where x=θ−π6
Solve the above inequality using graphs.
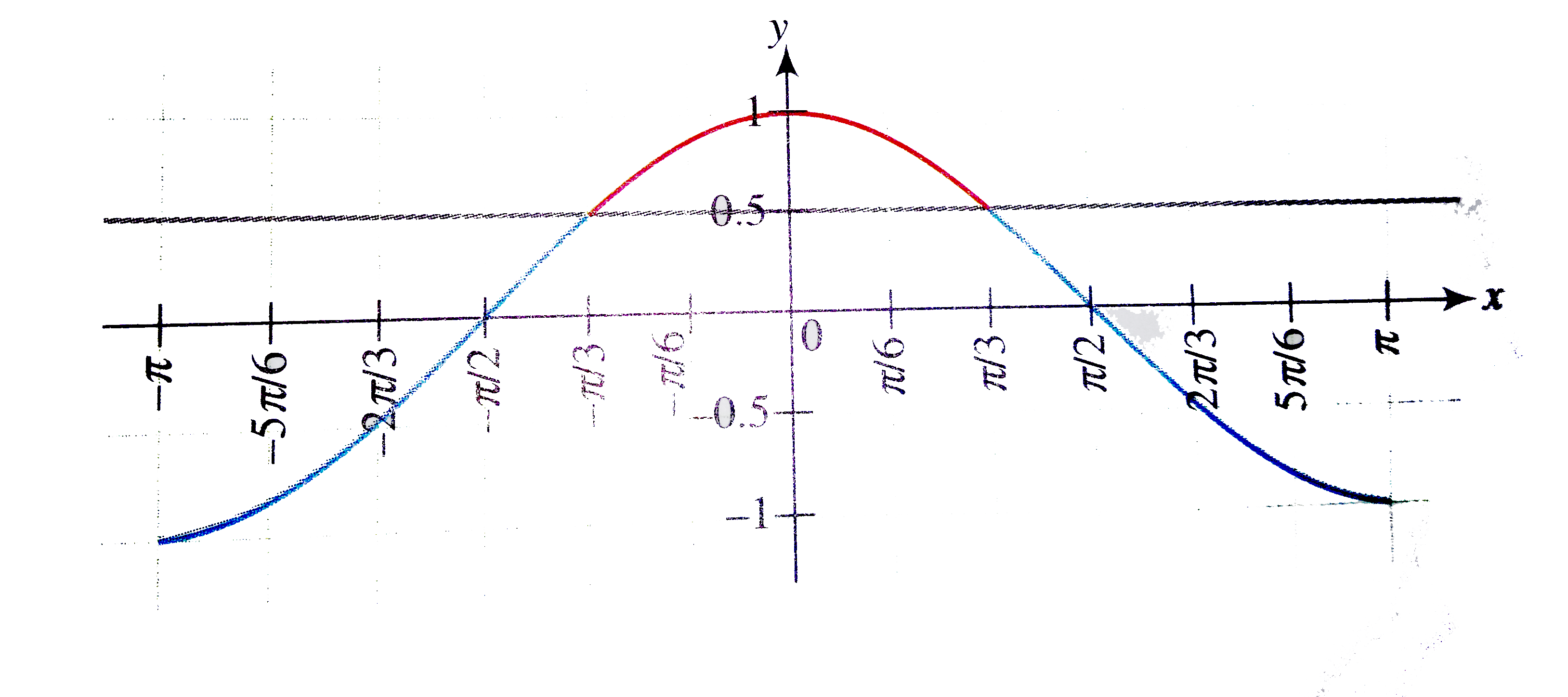 From the figure,
From the figure,
−π/3≤θ−π/6≤π/3
⇒ −π/6≤θ≤π/2
|
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
Similar Questions
Knowledge Check
The set solution satisfying inequality sinθ+√3cosθ≥1, -pi
Aθ∈[π3,π2]Bθ∈[−π6,π2]Cθ∈[π6,π2]DNone of the theseIf cosθ+sinθ=√2cosθ , then cosθ−sinθ is
A√2tanθB−√2cosθC−√2sinθD√2sinθ
Solve √√3cotθ<1
View Solution√3cosθ+sinθ=2
View SolutionIf cosθ+sinθ=√2cosθ,then find the value of cosθ−sinθsinθ.
View SolutionSolve: sin4θ=sinθ
View SolutionFind the number of solution of the equation 2sinθ−sin3θ1+cosθ+3cosθ+cos3θ1−sinθ=4√2cos(θ+π4)
in the interval (−10π,8π].
View SolutionSolve secθ+1=(2+√3)tanθ, 0<θ<2π
View Solution
