Rod of m and length l is free to rotate about point U in vertical plane. A particle having same mass m moving horizontally with velocity v0 his the rod perpendicular at distance l4 from the top end 'O' and stops. Find impulse due to hinge on the rod due to collision.
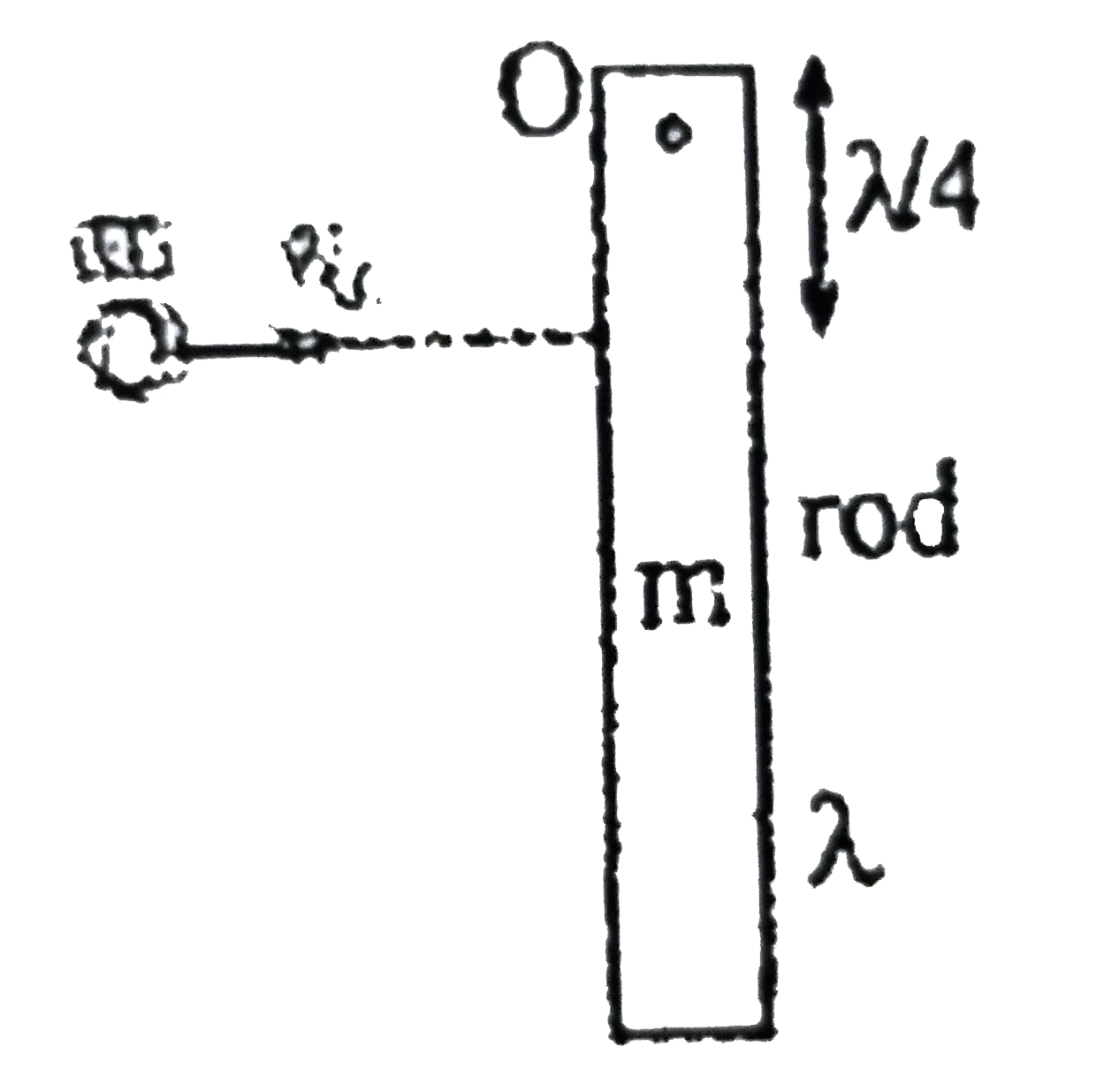
mv019
−10mv019
mv0
5mv08
mv0×l4=ml23ω
implse =mv0−m3v04l×l2
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)32videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)3videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C4videos
TEST PAPERS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
A uniform rod of mass M and length L lies on a frictionless horizontal plane. A particle of same mass M moving with speed v0 perpendicular to the length of the rod strikes the end of the rod and sticks to it. Find the velocity of the center of mass and the angular velocity about the center of mass of (rod + particle) system.
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View Solution
Knowledge Check
- Question 1 - Select One
A uniform rod of mass m and length l is hinged at upper end. Rod is free to rotate in vertical plane. A bail of mass m moving horizontally with velocity v0 collides at lower end of rod perpendicular to it and sticks to it. The minimum velocity of the ball such that combined system just completes the vertical circle will be
A2[√2gl]B√2glC2[√gl]D√gl - Question 2 - Select One
A rod of mass m and length l in placed on a smooth table. An another particle of same mass m strikes the rod with velocity v0 in a direction perpendicular to the rod at distance x(<l/2) from its centre . Particle sticks to the end. Let ω be the angular speed of system after collision , then
Find the maximum possible value of impulse (by varying x) that can be imparted to the particle during collision. Particle still sticks to the rod.Amv02B2mv03C3mv04D4mv05 - Question 3 - Select One
A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the rod with respect to C before the collisionAMvM+mBmvM+mC2mvM+mD2MvM+m

A uniform rod of mass 3 m and length l is lying on a smooth horizontal surface. Two particle of mass m and 2 m moving with speed 2v0 and v0 in the opposite directly hit the rod perpendicularly at a distance l3 and l6 from the midpoint O of the rod ad stick to it after collision. if the loss in kinetic energy of the system due to collision is n5mv20 find the value of n.View SolutionA uniform rod of mass m and length l can rotate freely on a smooth horizontal plane about a vertical axis hinged at point H. A point mass having same mass m coming with an initial speed u perpendicular to the rod, strikes the rod and sticks to it at a distance of 3l4 from hinge point. Theangular velocity of the rod just after collision is 36unl. Find the value of n.
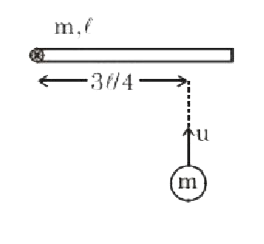 View Solution
View SolutionA rod of mass m,length l pivoted at its centre is free to rotate in a vertical plane.The rod is at rest and is in vertical position.A bullet of mass m/2 moving horizontally with speed v strikes and sticks to one end of the rod. Angular velocity of system just after collision is
View SolutionA uniform rod of mass M and length L lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance L/6 from the center and stops after the collision. Find
(a) the velocity of center of mass of rod and
(b) the angular velocity of the rod about its center just after collision.View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the particle with respect to C before the collisionView Solution

