A sphere resting in a smooth V sthaped groove and subjected to a spring force, is shown in the figure. The spring is compressed to a length of 100mm from its freelength of 150mm. If the stiffness of spring K=2N/mm. the contant reaction RL and RM at the points L andM respectively are
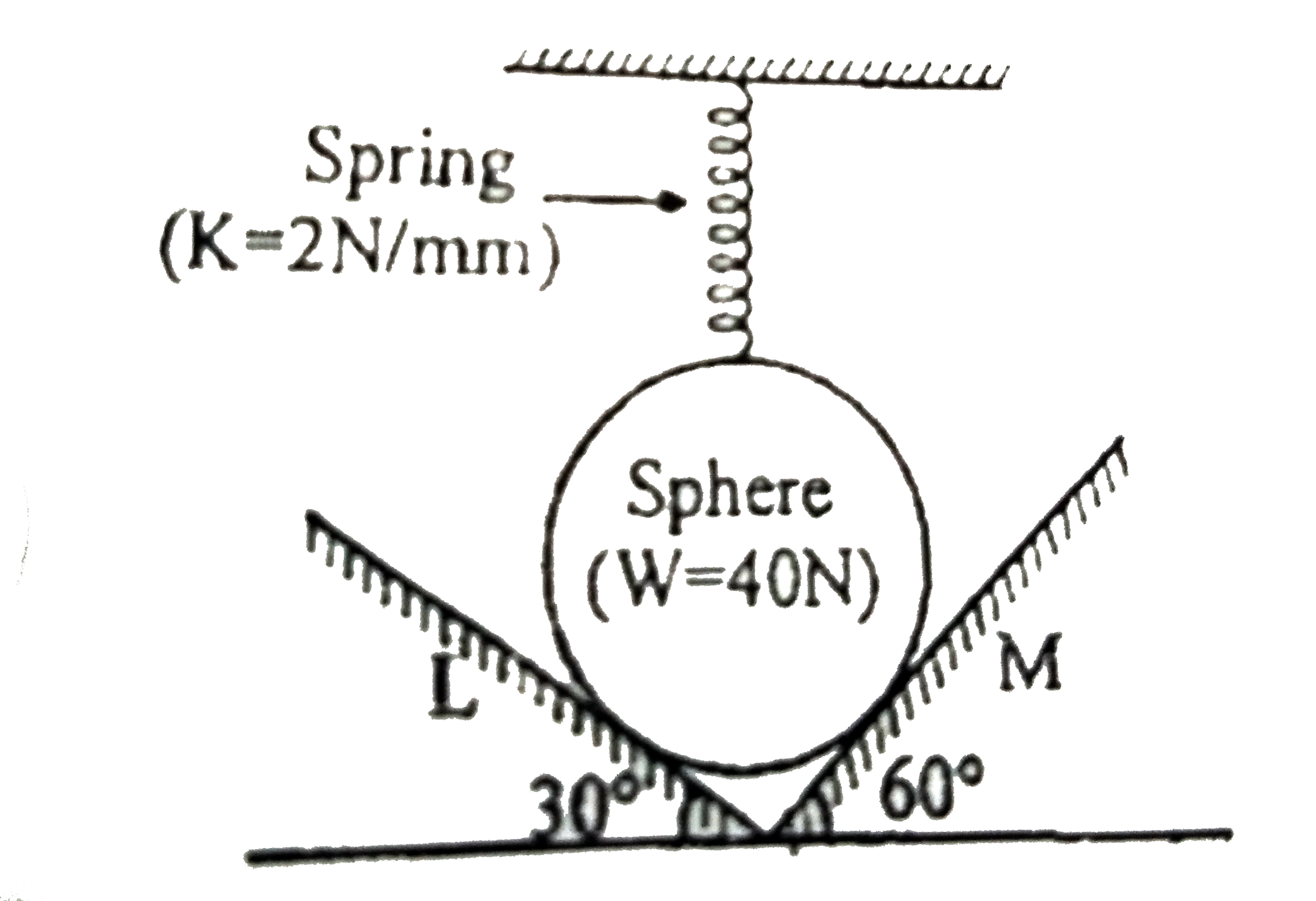
RL=121.24N and RM=80N
RL=121.24N and RM=70N
RL=131.24N and RM=60N
RL=131.24N and RM=80N
Compression of spring S=150-100=50
mm
∑P=0 (since the force are in equilibrium)
R2cos60∘−RMcos30∘=0
⇒RL=1.732RM. . . .(1)

RLsinθ−PS−W−RMsin30∘=0
RM=70NRjL=1.732=70=121.24N
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)32videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)3videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C4videos
TEST PAPERS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
A particle of mass m is moving with a constant speed v in a circular path in a smooth horizontal plate (plan of the paper ) by a spring force as shown in figure If the natural length of the spring is l0 and stiffeness of the spring is k find the elongation of the spring
 View Solution
View Solution
A block of mass 200 g is given velocity 2(m)/(s) on a horizontal surface as shown in the figure. Find the maximum compression of spring of spring constant k=100(N)/(m)View Solution
Knowledge Check
- Question 1 - Select One
A block of mass M is kept on a smooth surface and touches the two springs as shown in the figure but not attached to the springs. Initially springs are in their natural length. Now, the block is shifted (l0/2) from the given position in such a way that it compresses a spring and released. The time - period of oscillation of mass will be
 Aπ2√MkB2π√M5kC3π2√MkDπ√M2k
Aπ2√MkB2π√M5kC3π2√MkDπ√M2k - Question 2 - Select One
From the fixed pulley, masses 2kg, 1kg and 3kg are suspended as shown in the figure. Find the extension in the spring if k=100N/m. (Neglect oscillations due to spring)
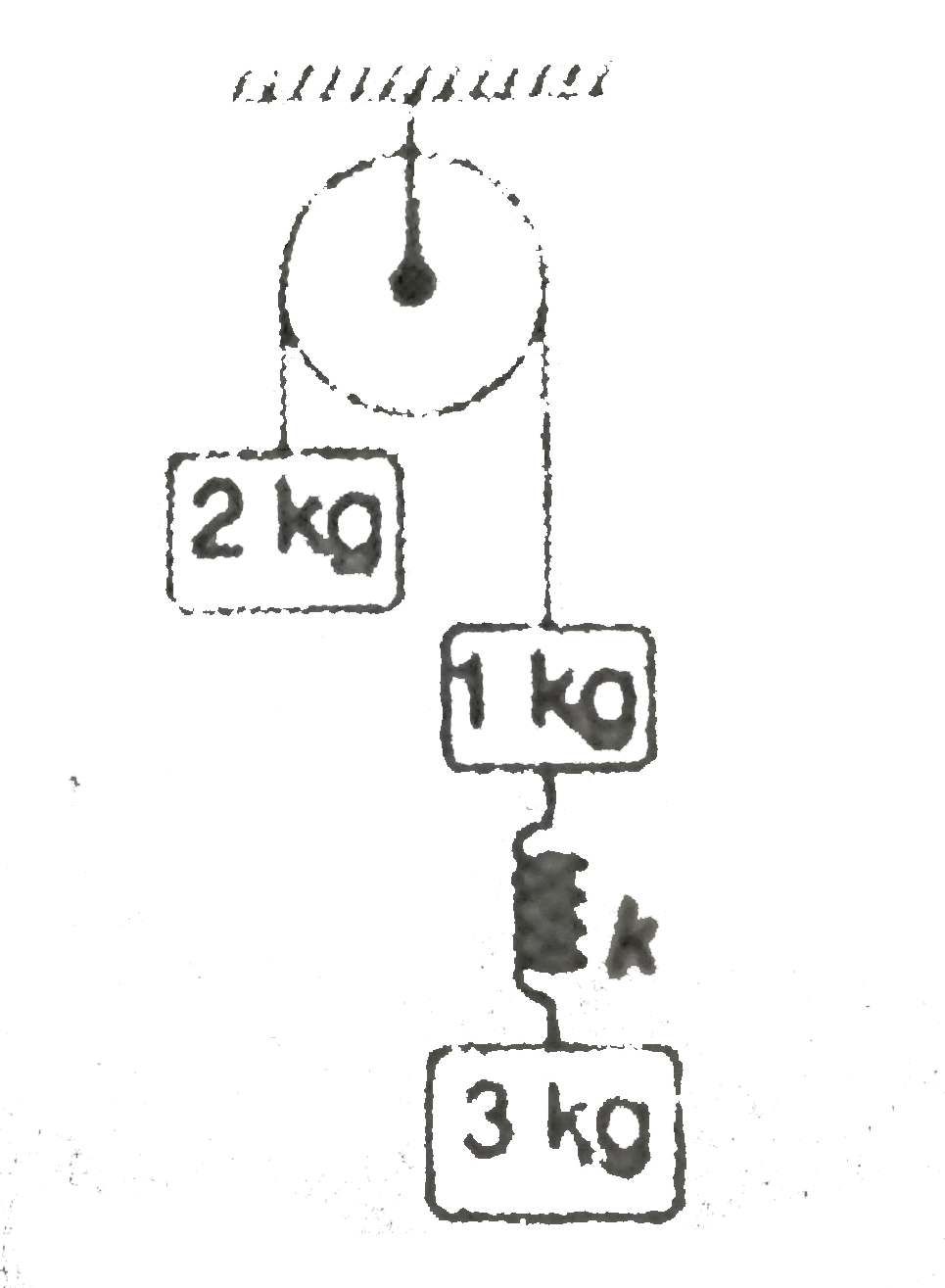 A0.1mB0.2mC0.3mD0
A0.1mB0.2mC0.3mD0 - Question 3 - Select One
A block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is
 A2π√mkB(π+4)√mkC(1+π)√mkDNone of these
A2π√mkB(π+4)√mkC(1+π)√mkDNone of these
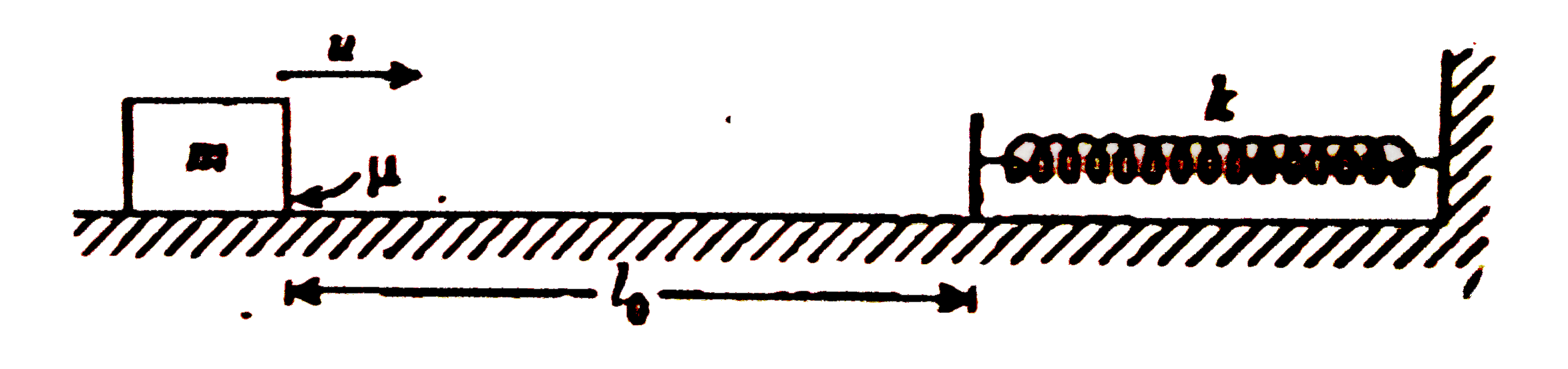
Figure. shows a rough horizontal plane which ends in a vertical wall, to which a spring is connected, having a force constant k. Initially spring is in its relaxed state. A block of mass m starts with an initial velocity u towards the spring from a distance l0 from the end of spring shown. When block strikes at the end ofthe spring, it compresses the spring and comes to rest. Find the maximum compression in the spring. The friction coefficient between the block and the floor is μ..
 View Solution
View SolutionIn figure a spring with k=168N/m is in its relaxed length and is at the top of a frictionless incline of angle θ=37∘. The lower end of the incline is at distance D = 1 m from the end of the spring. A small blcok of mass 2 kg is pushed against the spring until the spring is compressed by 0.2 m and released from rest.
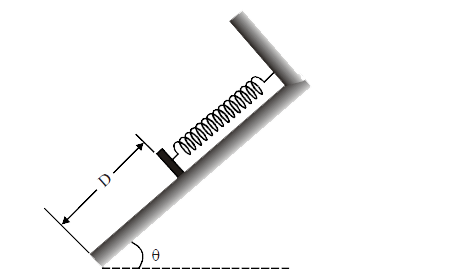
What is the speed of the block at the instant the spring returns to its relaxed length (which is when the block loses contact with the spring)?View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.

The maximum value of V0 for whic the disk will roll without slipping is-View SolutionA block of mass m=25kg on a smooth horizontal surface with a velocity →v=3ms−1 meets the spring of spring constant k=100N/m fixed at one end as shown in figure. The maximum compression of the spring and velocity of block as it returns to the original position respectively are.
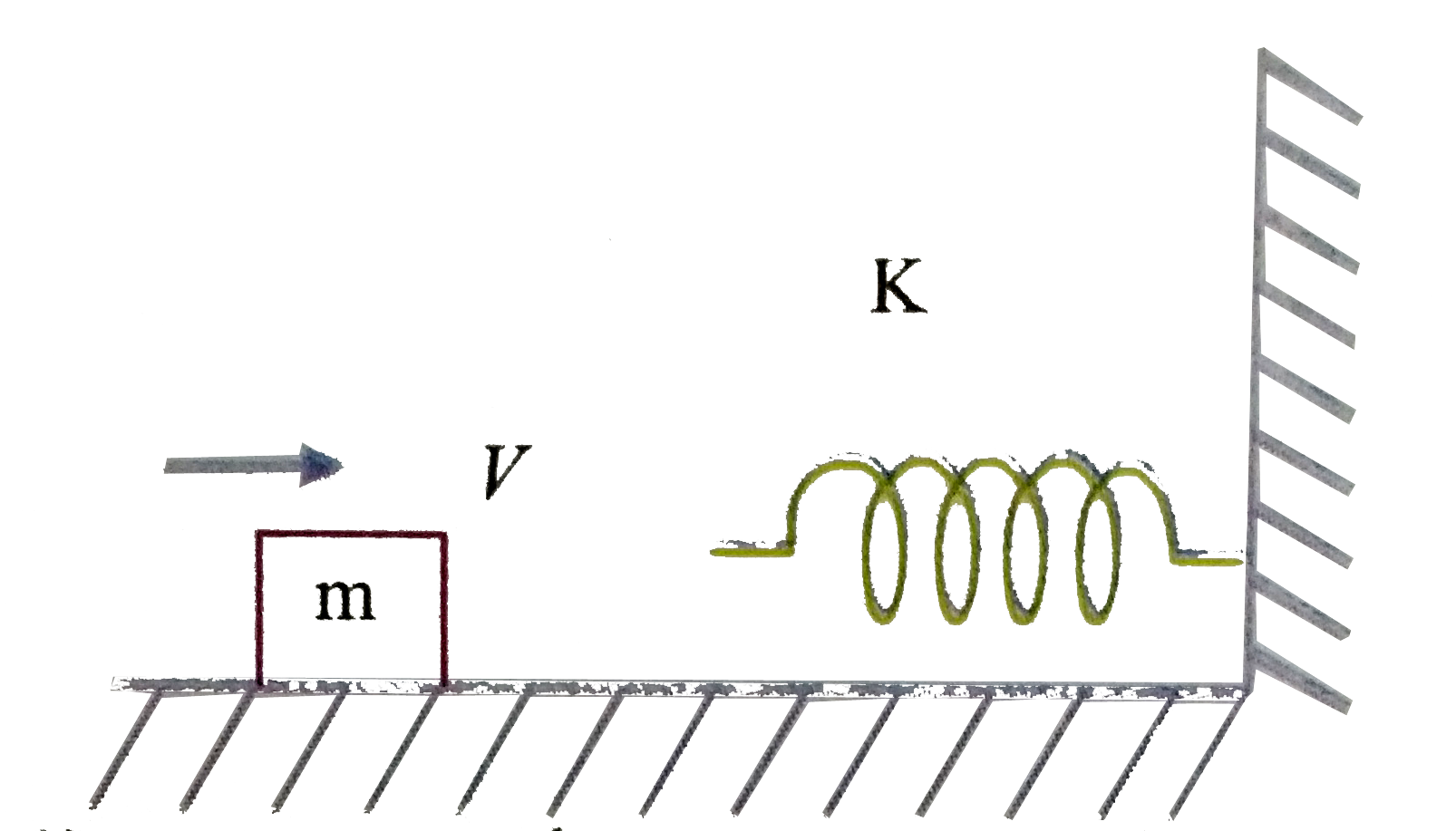 .View Solution
.View SolutionA thin uniform vertical rod of mass m and length l pivoted at point O is shown in Fig. The combined stiffness of the springs is equal to k. The mass of the springs is negligible. The angular frequency of small oscillation is
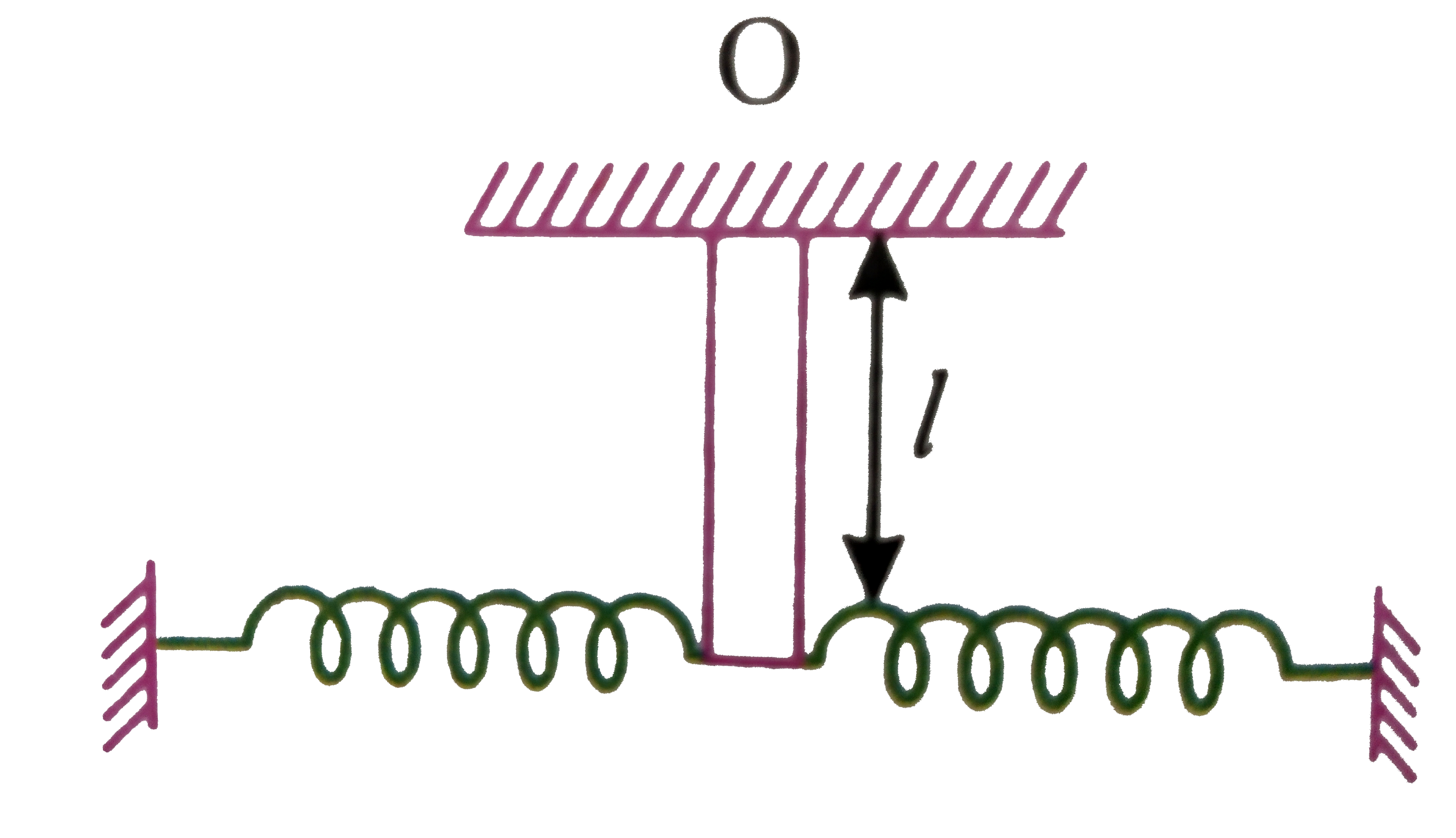 View Solution
View Solution

