Particles a and b move in opposite direction around a circle with same angular speed $ω$ , as shown. At t=0 they are both at the point $\to r = \to t \to j$ , where l is the radius of the circle. The magnitude angular velocity of 'a' w.r.t. 'b' at time t=t

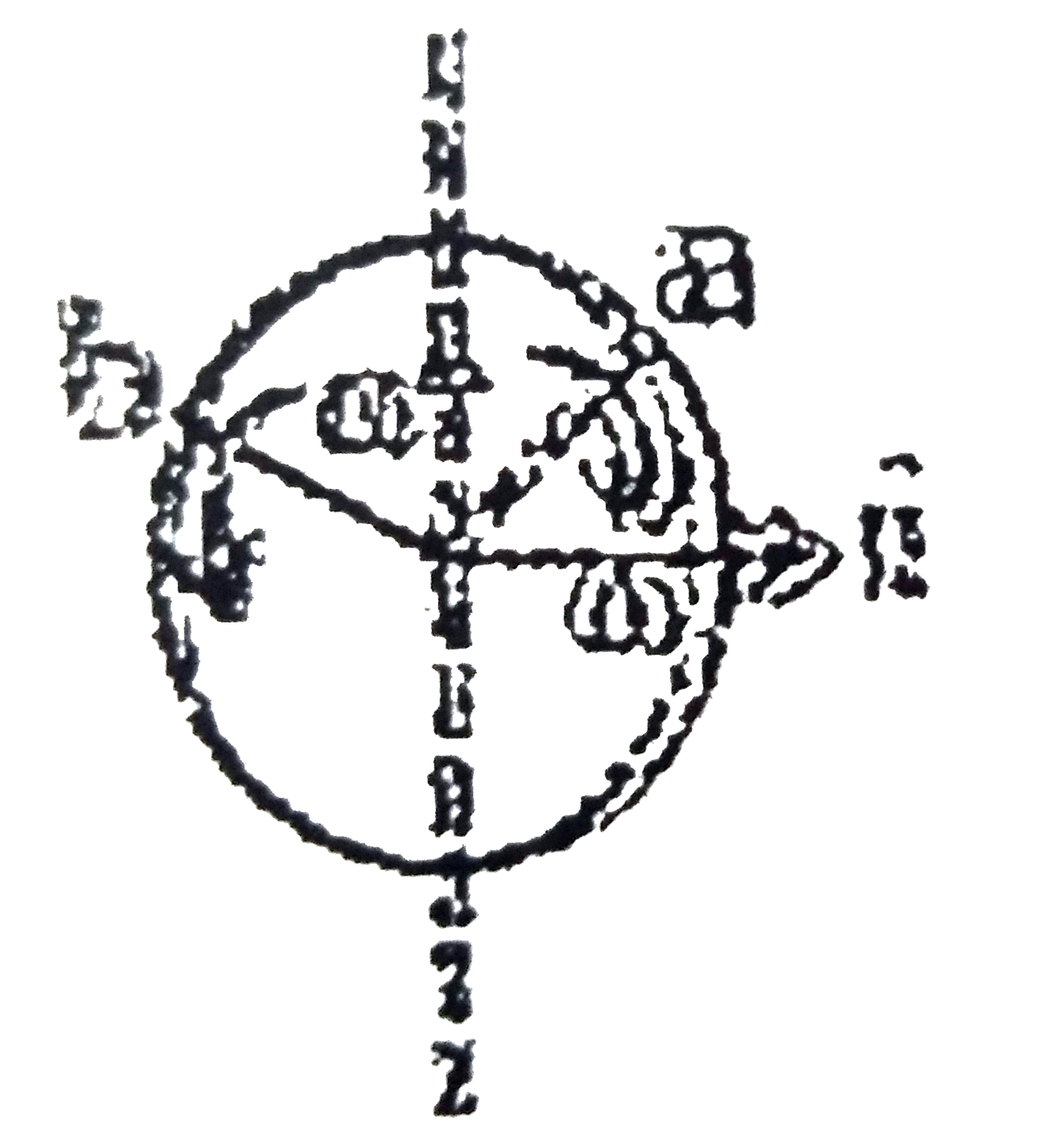
Zero

$ω cot (ω t)$

$ω sin ω t$

$2 ω$

Video Solution

Answer

Step by step video & image solution for Particles a and b move in opposite direction around a circle with same angular speed omega, as shown. At t=0 they are both at the point vecr=vect vecj, where l is the radius of the circle. The magnitude angular velocity of 'a' w.r.t. 'b' at time t=t by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Knowledge Check

Two particles P and Q are moving as shown in the figure. At this moment of time the angular speed of P w.r.t. Q is

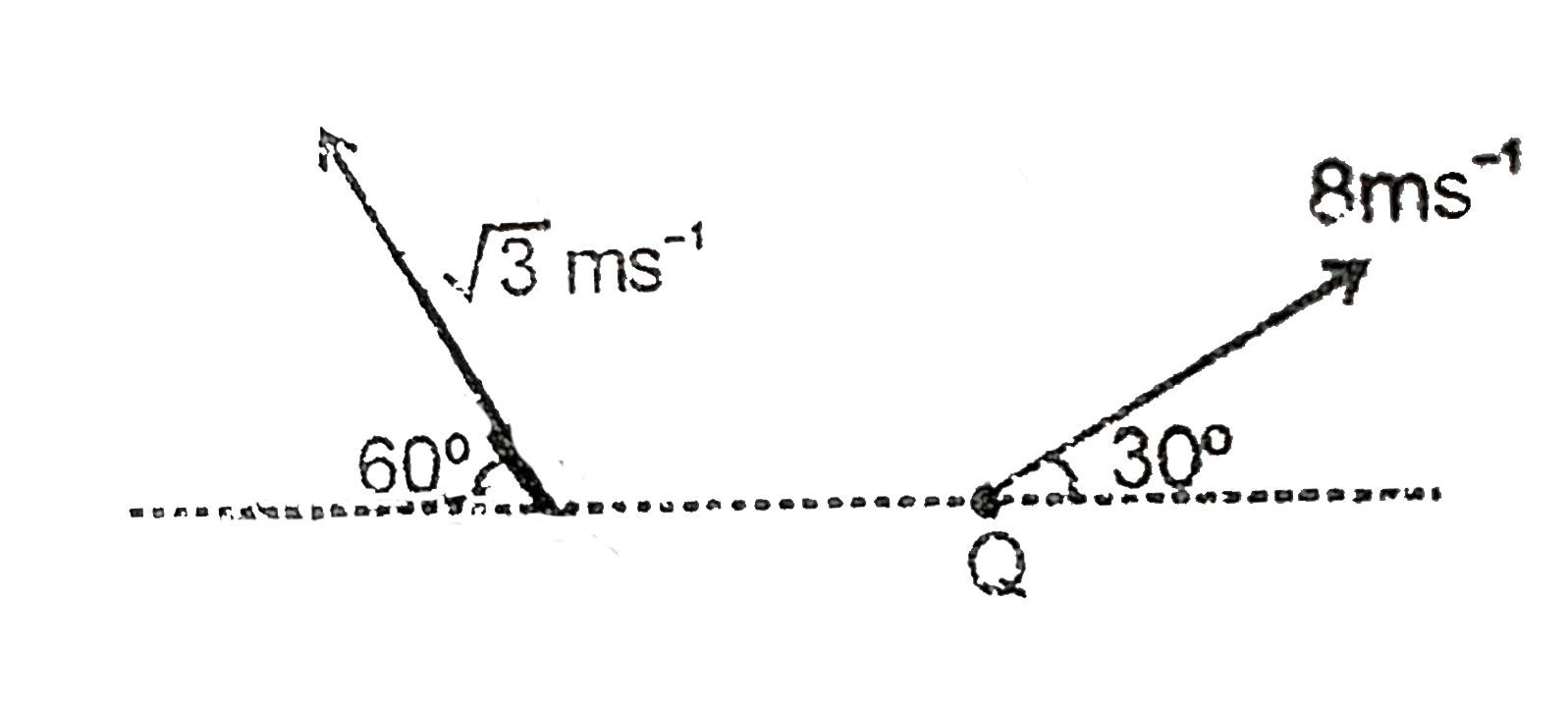A $5 {rads}^{- 1}$
B $4 {rads}^{- 1}$
C $2 {rads}^{- 1}$
D $1 {rads}^{- 1}$
Two particles A,B are moving on two concentric circles of radii $R_{1})$ and $R_{2}$ with equal angular speed $ω$ . At $t = 0$ ,their positions and direction fo motion are shown in the figure :

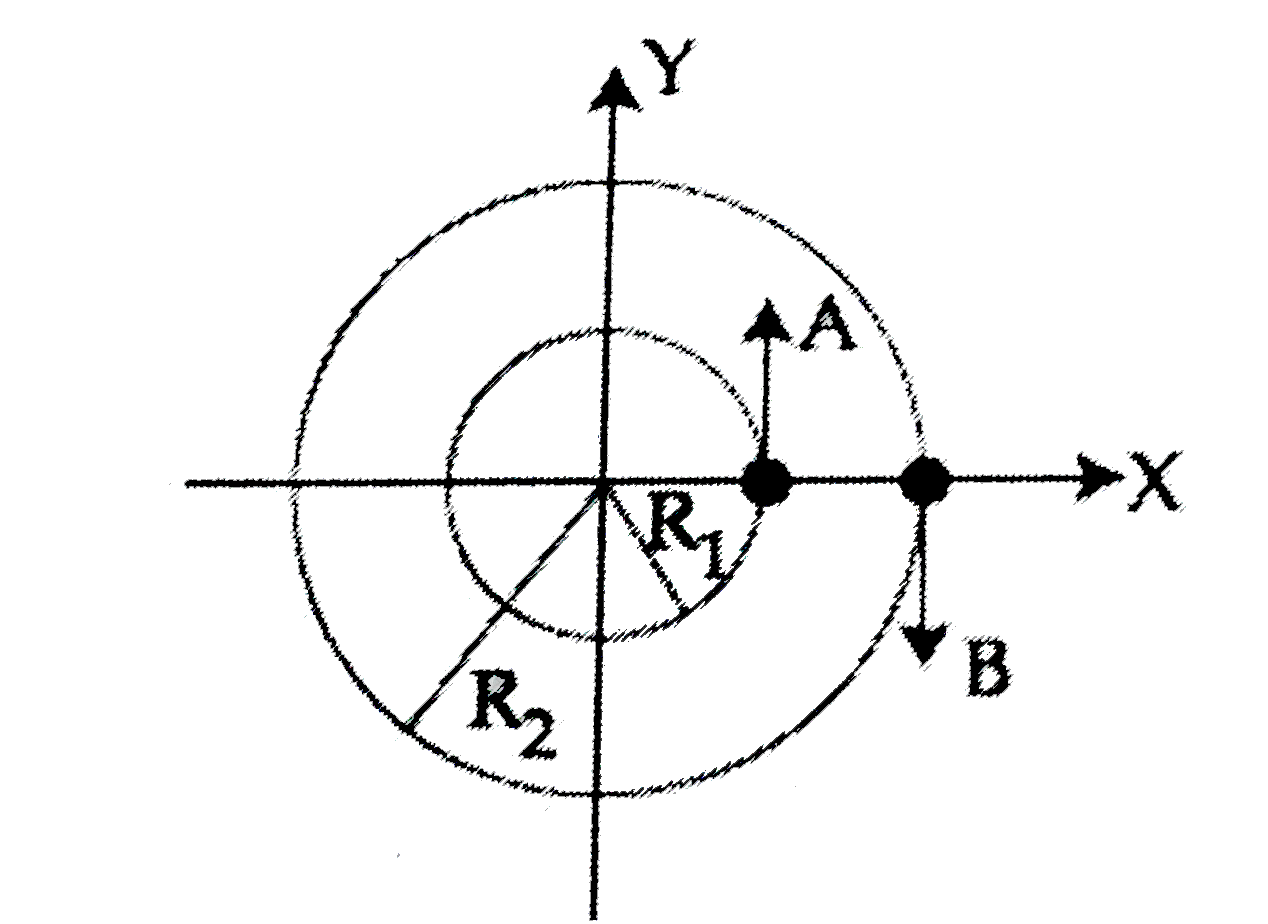A $ω (R_{1} + R_{2}) ˆ i$
B $- ω (R_{1} + R_{2}) ˆ i$
C $ω (R_{2} - R_{1}) ˆ i$
D $ω (R_{1} - R_{2}) ˆ i$
Two particles A,B are moving on two concentric circles of radii $R_{1})$ and $R_{2}$ with equal angular speed $ω$ . At $t = 0$ ,their positions and direction fo motion are shown in the figure :

A $ω (R_{1} + R_{2}) ˆ i$
B $- ω (R_{1} + R_{2}) ˆ i$
C $ω (R_{2} - R_{1}) ˆ i$
D $ω (R_{1} - R_{2}) ˆ i$

BANSAL-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile

Particles a and b move in opposite direction around a circle with same angular speed ω, as shown. At t=0 they are both at the point →r=→t→j, where l is the radius of the circle. The magnitude angular velocity of 'a' w.r.t. 'b' at time t=t

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two particles P and Q are moving as shown in the figure. At this moment of time the angular speed of P w.r.t. Q is

Two particles A,B are moving on two concentric circles of radii R1) and R2 with equal angular speed ω. Att=0,their positions and direction fo motion are shown in the figure :

Two particles A,B are moving on two concentric circles of radii R1) and R2 with equal angular speed ω. Att=0,their positions and direction fo motion are shown in the figure :

BANSAL-TEST PAPERS-PHYSICS

Particles a and b move in opposite direction around a circle with same angular speed $ω$ , as shown. At t=0 they are both at the point $\to r = \to t \to j$ , where l is the radius of the circle. The magnitude angular velocity of 'a' w.r.t. 'b' at time t=t

Two particles A,B are moving on two concentric circles of radii $R_{1})$ and $R_{2}$ with equal angular speed $ω$ . At $t = 0$ ,their positions and direction fo motion are shown in the figure :

Two particles A,B are moving on two concentric circles of radii $R_{1})$ and $R_{2}$ with equal angular speed $ω$ . At $t = 0$ ,their positions and direction fo motion are shown in the figure :