A bead of mass m is atached to a spring of natural length 3R4 with other end of it fixed at O.The bead moves in a track of which part ABC is semicircular of radius R and part CDA varies from R to R2 and then again to R. The bead is in equilibrium at position D and starts moving downward. Find the ratio of normal reaction on the bead to the cetrifugal force at the bottom most position.

2
12
1,0
13
In position D spring is in equilibrium. ltbr> N+mg−F=0. . . (1)
in bottom most position.
N+f−mg=mv22. . . .(2)
[since spring is elongated]
where F=kx and x=3R4−R2=R4in
position D
and x=R−3R4=R4 in bottom position
From 1 and 2
N+(N+mg)−mg=mv2r
2N=mv2r
Nmv2/r=12
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A bead of mass m is attached to one end of a spring of natural length R and spring constant K=(√3+1)mgR. The other end of the spring is fixed at a point A on a smooth vertical ring of radius R as shown in fig. The normal reaction at B just after it is released to move is
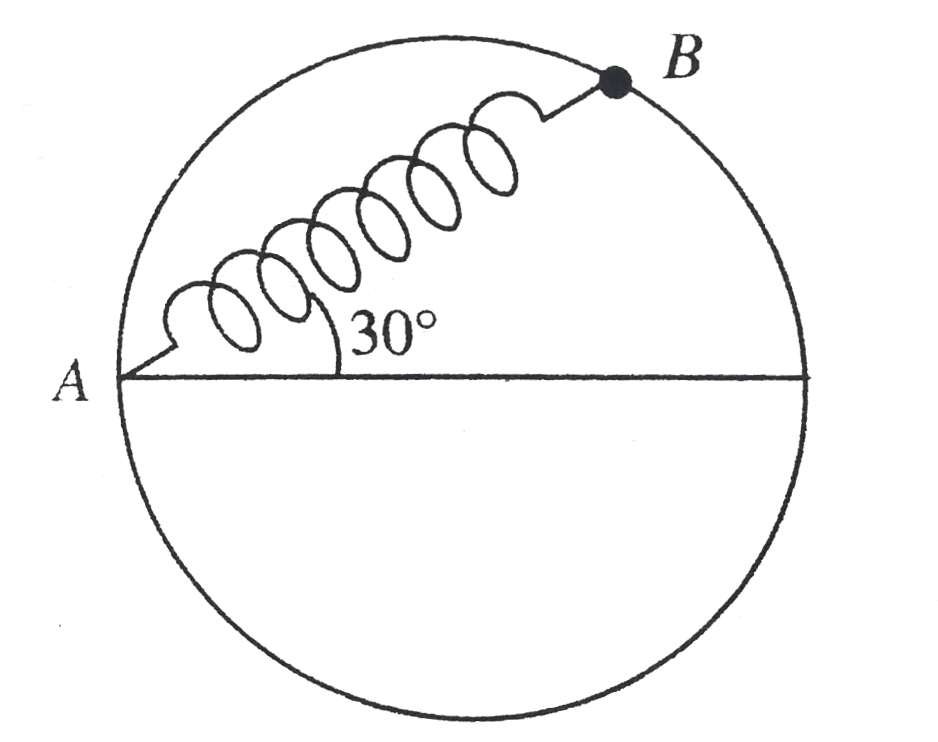
View SolutionFind the ratio of the first quantity to the second.
25 beads, 40 beads
View Solution
Knowledge Check
A Bead of mass m is attached to one end of a spring of natural length 'R' and spring cosntant 'k=(√3+1)mgR'. The other end of the spring is fixed at point 'A' on a smooth vertical ring of radius 'R' as shown
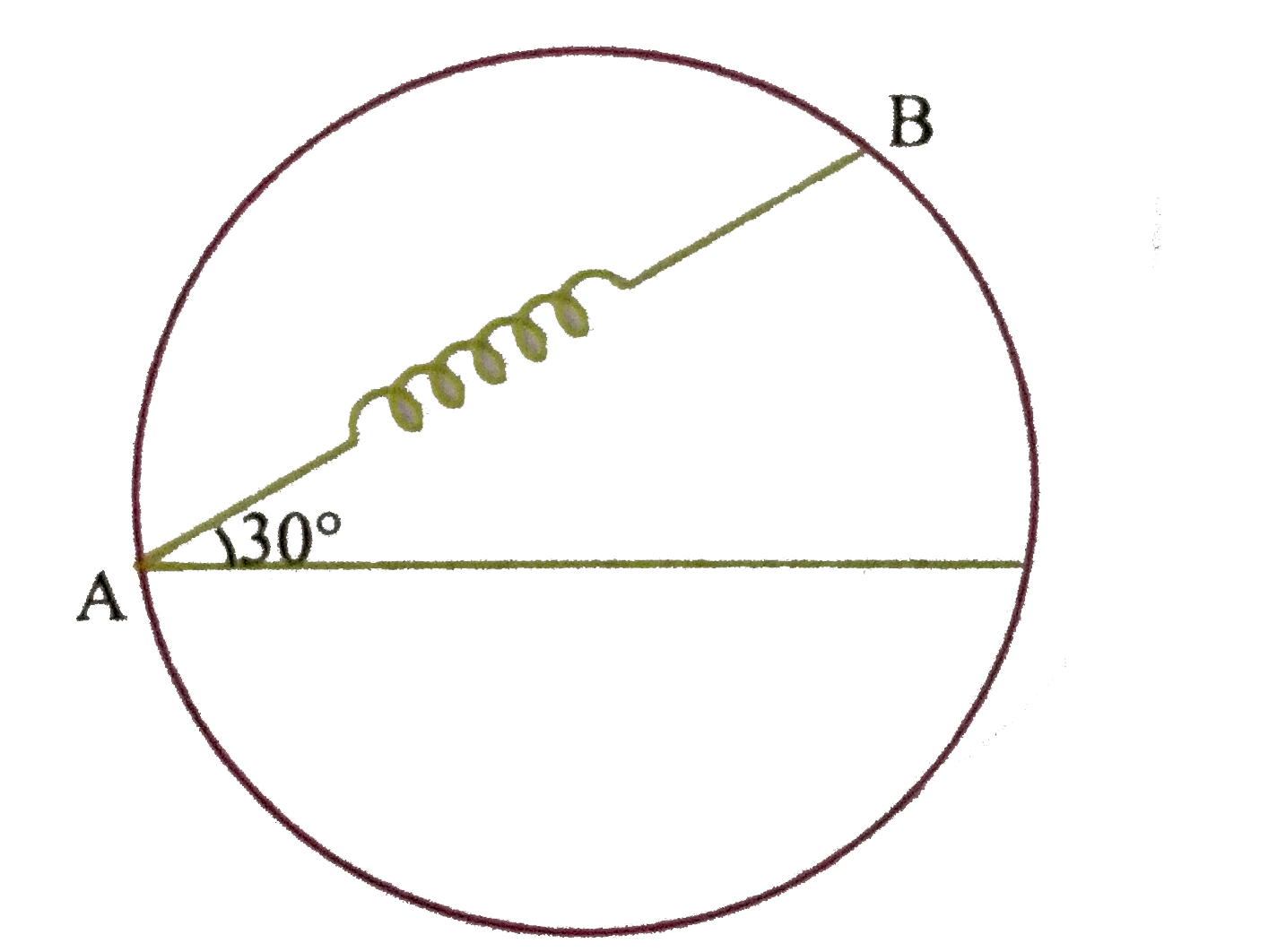 AThe normal reaction at 'B' just after the bead is released to move is:3√3mg2BThe tangential acceleration of the bead just after it is released to move is :g/2CThe normal reaction at 'B' just after the bead is released to move is :3mg2DJust after the bead is released to move the normal acceleration and Tangential acceleration are numerically equal.
AThe normal reaction at 'B' just after the bead is released to move is:3√3mg2BThe tangential acceleration of the bead just after it is released to move is :g/2CThe normal reaction at 'B' just after the bead is released to move is :3mg2DJust after the bead is released to move the normal acceleration and Tangential acceleration are numerically equal.A bead of mass 'm' is attached to one end of a spring of natural length R & spring constant k=(√3+1)R. The other end of the spring is fixed at point A on a smooth vertical ring of radius R as shown. The normal reaction at B just after it is released to move is
 A√3mgB3√3mgCmg2D3√3mg2
A√3mgB3√3mgCmg2D3√3mg2A Bead of mass m is attached to one end of a spring of natural length 'R' and spring cosntant 'k=(√3+1)mgR'. The other end of the spring is fixed at point 'A' on a smooth vertical ring of radius 'R' as shown
 Amg/2B√3mgC3√3mgD3√3mg2
Amg/2B√3mgC3√3mgD3√3mg2
A bead of mass m can slide without friction along a vertical ring of radius R. One end of a spring of force constant k=3mgR is connected to the bead and the other end is fixed at the centre of the ring. Initially, the bead is at the point A and due to a small push it starts sliding down the ring. If the bead momentarily loses contact with the ring at the instant when the spring makes an angle 60∘ with the vertical, then the natural length of the spring is
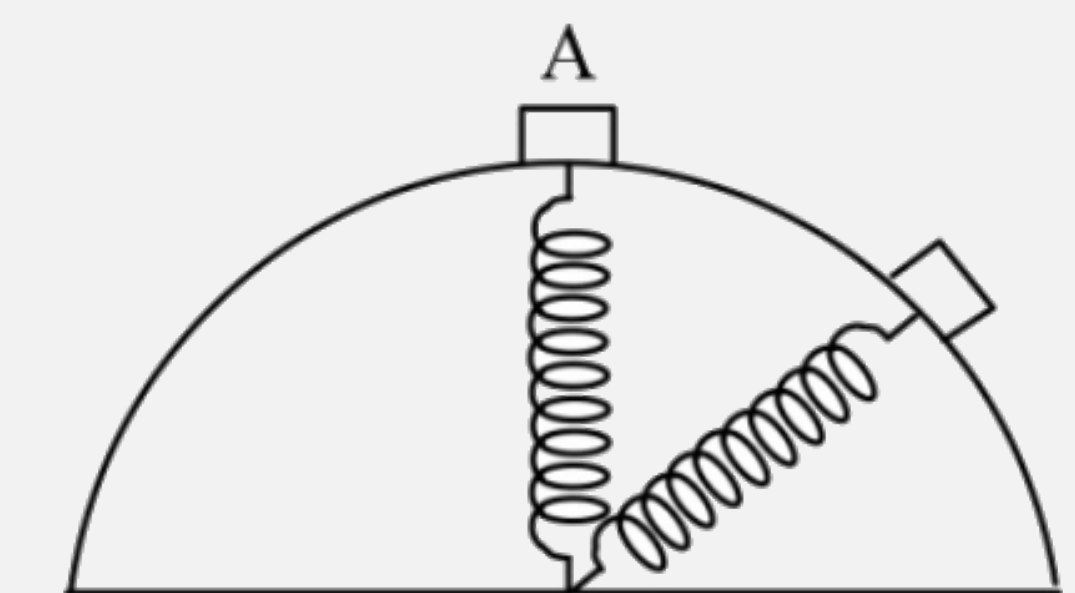
View SolutionA bead of mass m can slide without friction along a vertical ring of radius R. One end of a spring of force constant k=3mgR is connected to the bead and the other end is fixed at the centre of the ring. Initially, the bead is at the point A and due to a small push it starts sliding down the ring. If the bead momentarily loses contact with the ring at the instant when the spring makes an angle 60∘ with the vertical, then the natural length of the spring is

View SolutionTwo identical beads each have a mass m and charge q. When placed in a hemispherical bowl of radius R with frictionless, non-conducting walls, the beads move, and at equilibrium they area distance R apart (figure). Determine the charge on each bead.
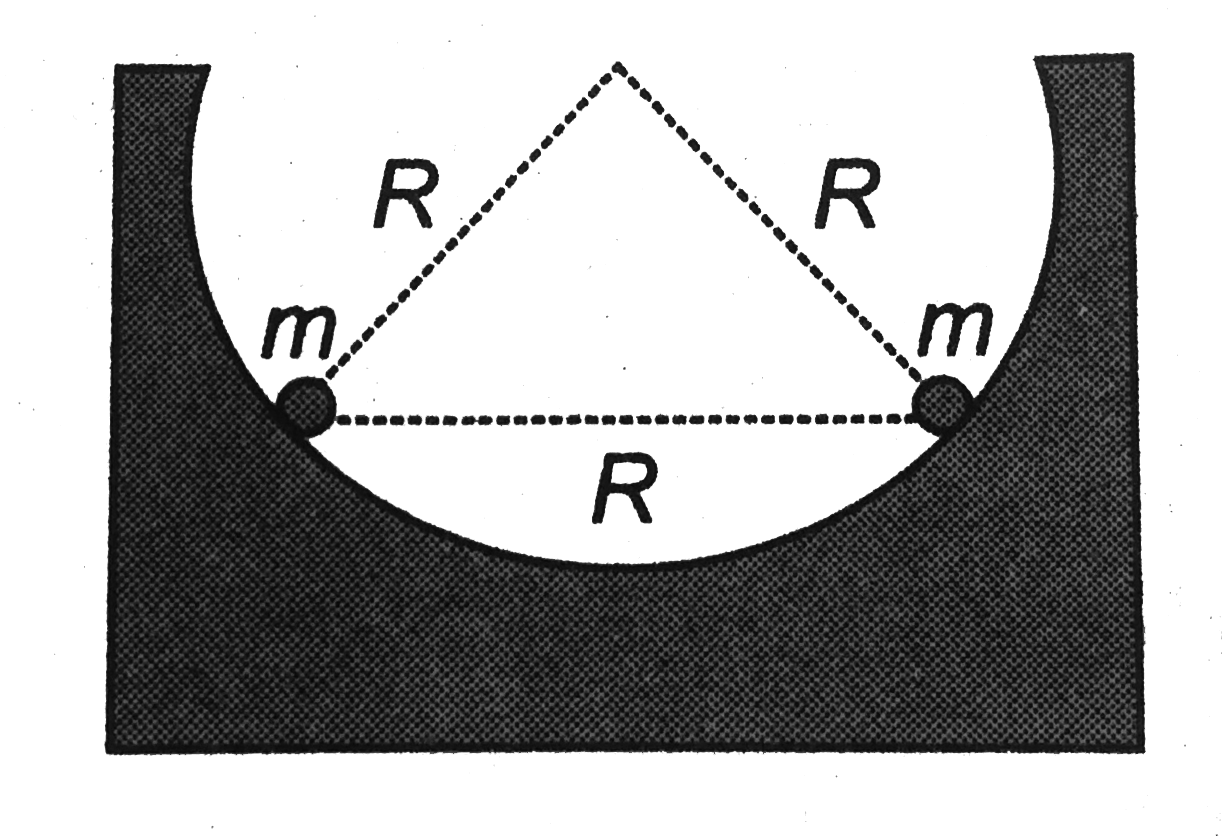
View SolutionTwo identical beads each have a mass m and charge q. When placed in a hemispherical bowl of radius R with frictionless, non-conducting walls, the beads move, and at equilibrium they area distance R apart (figure). Determine the charge on each bead.

View SolutionA rod can rotate in a horizontal plane about its one end. A bead which can move along the rod is placed at certain distance from the axis or rotation. The bead does not to friction. The rod has a constant angular acceleration
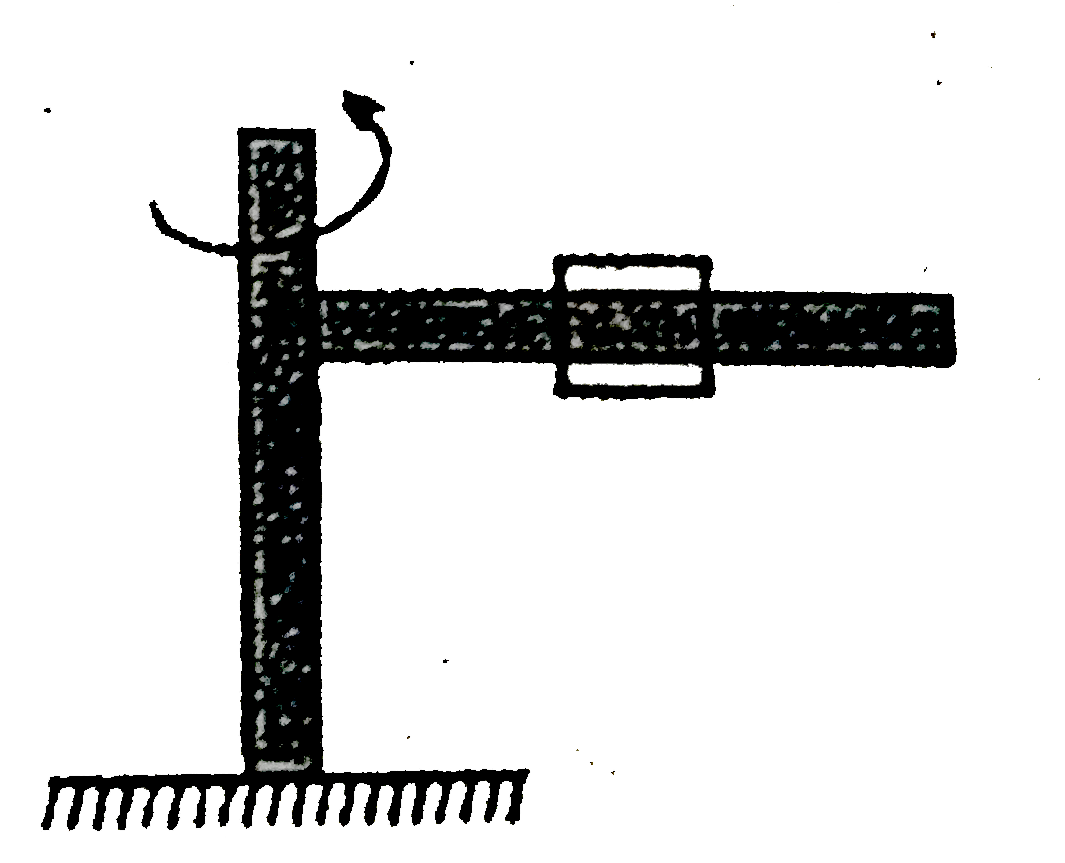
A. the normal reaction on the bead will be constant h magnitude and direction both
B. the magnitude of the normal reaction on the bead will be variable
C. the magnitude of friction force on the bead will be constant
D. the magnitude of friction force on the bead will be variable
View Solution
