On a disc of mass 10 kg and diameter 40 cm , few forces are acting as shown in diagram . Find the torque acting and initial angular accceleration α of the disc .

Torque due to the followings forces are
(i) Due to 4N force →τ1=0.2×4Nm=0.8 Nm(acw)
(ii) Due to 9N force →τ2=0.2×9Nm=1.8 Nm (cw)
(iii) Due to 6N force →τ3=0 (s it passes through 0)
(iv) Due to 8N force →τ4=0.2×8×sin30∘=0.8NM (cw)
(v) Net torque =τ=0.8−1.8+0−0.8=−1.8Nm=1.8Nm (cw)
Now
α=τ/I1.812MR2=1.8×210×0.22
=3.610×00.4=9rad/s2 (cw)
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 1
9 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EVALUATE YOURSELF - 4
11 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI
78 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)
19 Videos
Similar Questions
Two equal and opposite forces are allplied tangentially to a uniform disc of mass M and radius R as shown in the figure. If the disc is pivoted at its centre and free to rotate in its plane, the angular acceleration of the disc is :

View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View Solution
Knowledge Check
A disc of mass 2 kg and diameter 40 cm is free to rotate about an axis passing through its centre and perpendicular to its plane. If a force of 50 N is applied to the disc tangentially Its angular acceleration will be
A100rad/s2B25rad/s2C250rad/s2D500rad/s2A uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is
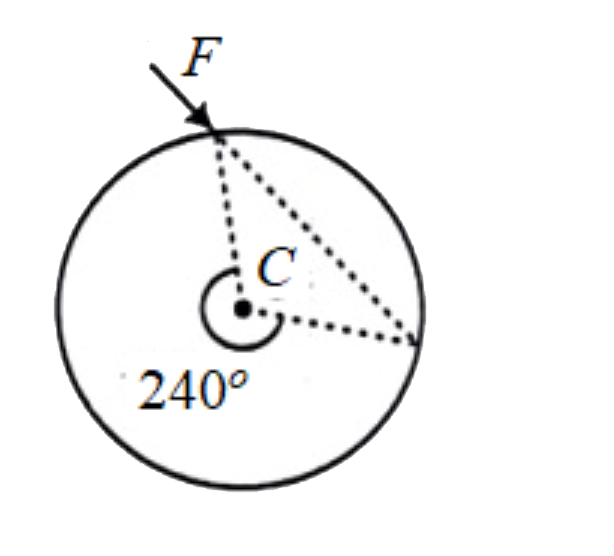 A√3FMRBFMRC2√3FMRDF2MR
A√3FMRBFMRC2√3FMRDF2MRA particle of mass M and radius of gyration K is rotating with angular acceleration α. The torque acting on the particle is
A12MK2αBMK2αCMK2αD14MK2α2
A uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View SolutionWhat constant torque should be appiled to a disc of mass 10kg and diameter 50cm so that it acquires an angular velocity of 2π rad/s in 4s ? The disc is initially at rest and rotates about an axis through the centre of the disc and in a plane perpendicular to the disc.
View SolutionConsider a disc of mass m and radius R placed on a rough plank of mass M which is turn is place on a smooth horizontal surface. Now plank is pulled by a force F and disc starts to roll on the plank.
If there is no friction any where then find
(a) Fricition force acting on the disc
(b) Angular acceleration of the disc

View SolutionConsider a disc of mass m and radius R placed on a rough plank of mass M which is turn is place on a smooth horizontal surface. Now plank is pulled by a force F and disc starts to roll on the plank.
If there is no friction any where then find
(a) Fricition force acting on the disc
(b) Angular acceleration of the disc

View SolutionA particle of mass M and radius of gyration K is rotating with angular acceleration α. The torque acting on the particle is
View Solution
