In the above figure , ¯¯¯¯¯¯ABand¯¯¯¯¯¯AC are equal chords and ¯¯¯¯¯¯OD is perpendicular to ¯¯¯¯¯¯AC . If ∠COD=60∘, then the angle between the chords is ______ .
A
30∘
B
60∘
C
90∘
D
Cannot be determined
Video Solution
Text Solution
The correct Answer is:B
(i) Triangles OAC and OAB are congruent. Triangle OAD and OCD are congruent.
(ii) Join OA and OB.
(iii) ∠AOC=2∠COD and ∠BOA=∠COA.
(iv) Use the above two results and find angles BAO and CAO.
(v) Angle between the chords =∠BAO+∠CAO.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level 220videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level 37videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Essay type Question3videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FormulaeEXERCISE - Level 37videos
Formulae
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICESEXERCISE - CONCEPT APPLICATION (Level 3)7videos
INDICES
Similar Questions
Knowledge Check
- Question 1 - Select One
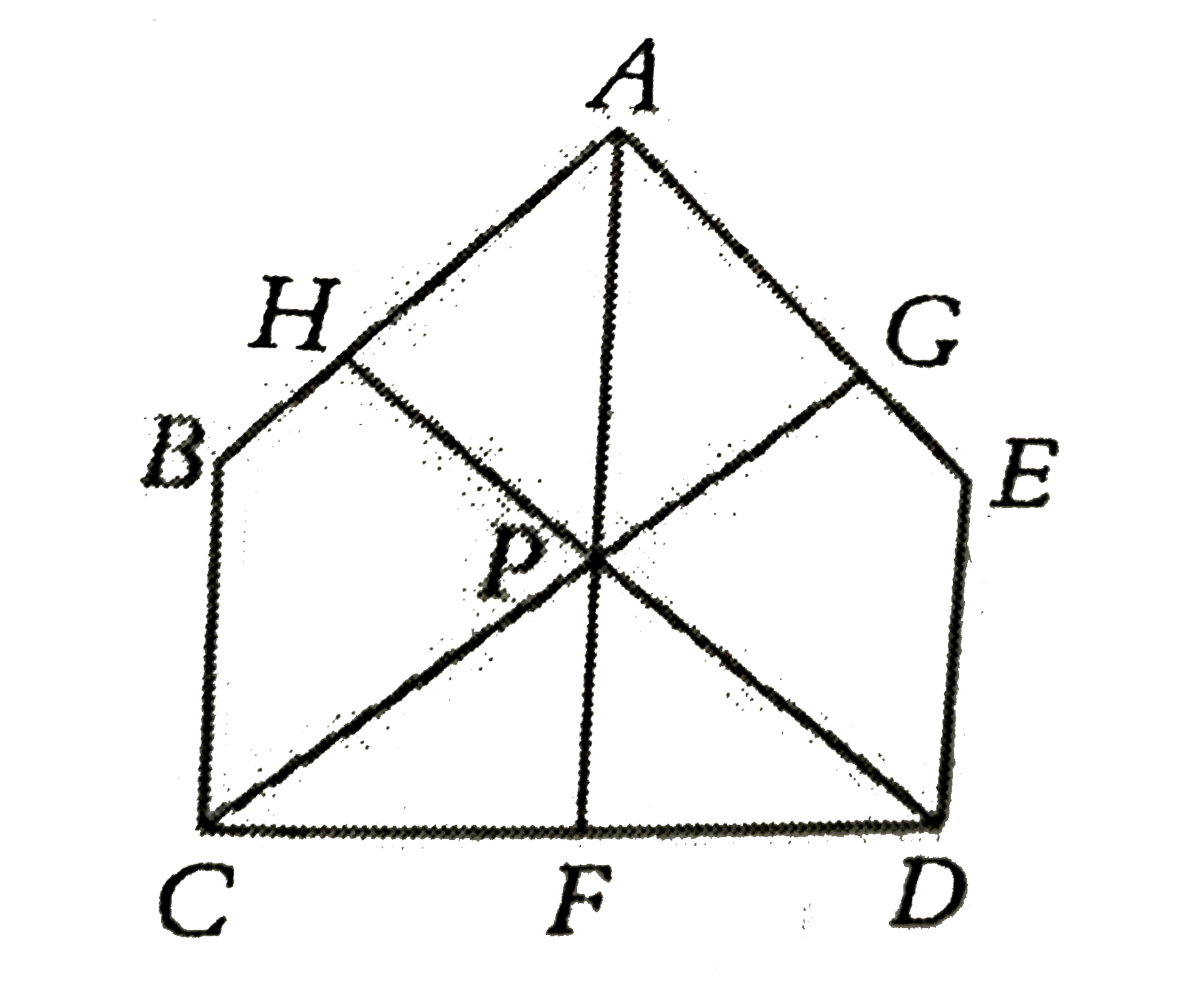
In the above figure, ¯¯¯¯¯¯AF∣∣∣∣¯¯¯¯¯¯ED,¯¯¯¯¯¯CG∣∣∣∣¯¯¯¯¯¯AB and ¯¯¯¯¯¯AE∣∣¯¯¯¯¯¯¯HD If ∠FPD=40∘, then ∠AED=A40∘B80∘C120∘D140∘ - Question 2 - Select One
In the figure given below , ¯¯¯¯¯¯ED∣∣∣∣¯¯¯¯¯¯ABand¯¯¯¯¯¯EF∣∣∣∣¯¯¯¯¯¯BC. If ∠FED=40∘and∠DEC=20∘ , then the angle made by ¯¯¯¯¯¯BC at the centre is _______.
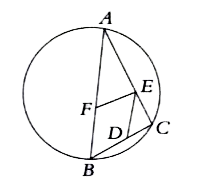 A20∘B40∘C60∘D80∘
A20∘B40∘C60∘D80∘ - Question 3 - Select One
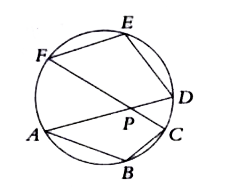
In the above figure (not to scale) ¯¯¯¯¯¯AB,¯¯¯¯¯¯BC,¯¯¯¯¯¯CF,¯¯¯¯¯¯DE,and¯¯¯¯¯¯FE are chords of the circle . If ∠ABC=100∘and∠FED=110∘ , then ∠FPA= _______.A20∘B30∘C40∘D70∘
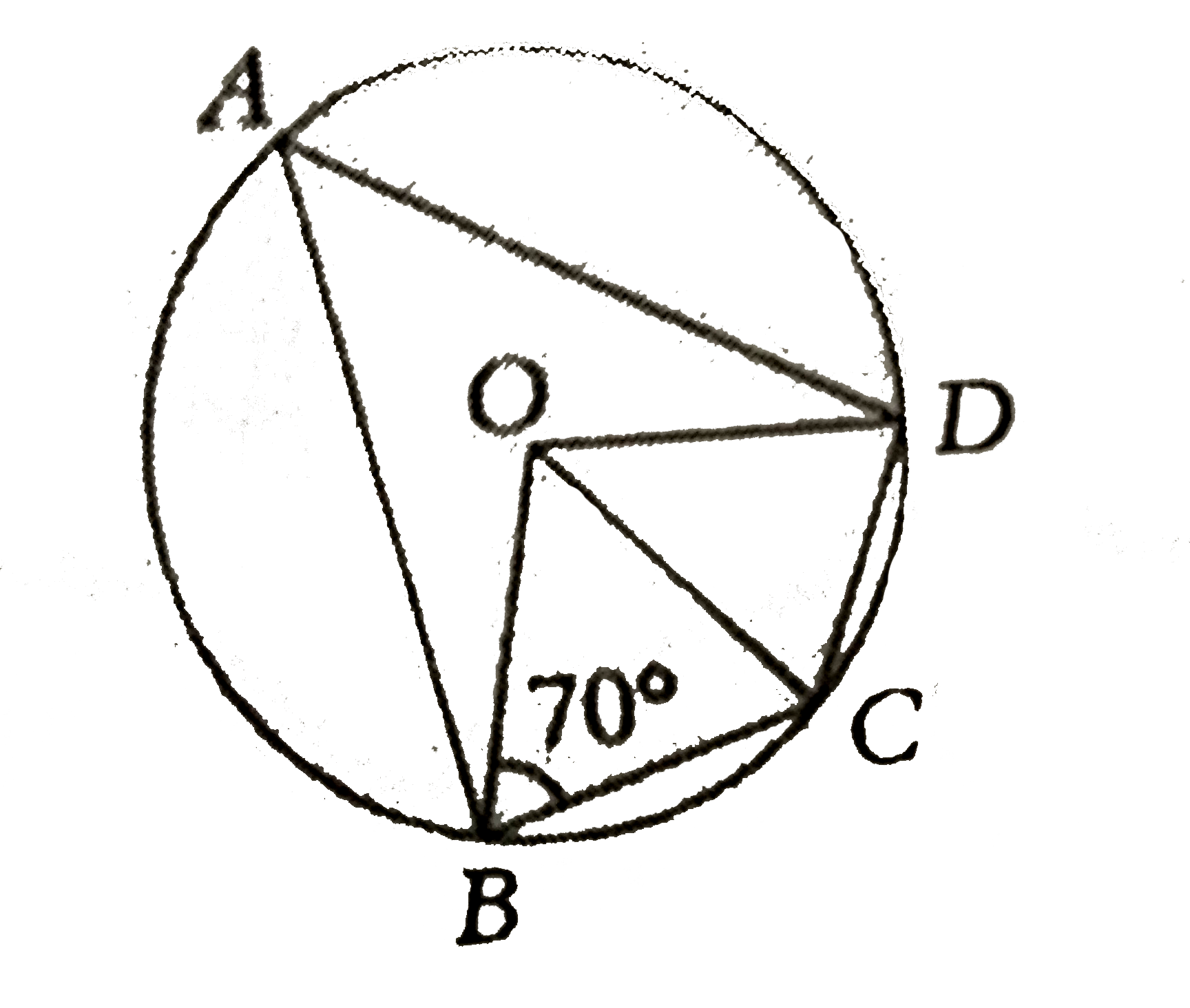
In the above figure (not to scale), O is the centre of the circle. ¯¯¯¯¯¯BC and ¯¯¯¯¯¯CD are equal chords. If ∠OBC=70∘ , then find ∠BAD.View SolutionIf |¯a|=5,∣∣¯b∣∣=3,|¯c|=4and|¯a| is perpendicular to ∣∣¯b∣∣and|¯c| such that the angle between ∣∣¯b∣∣and|¯c| is 5π6, then [¯a¯b¯c]=
View SolutionIn triangle ABC, if 2¯¯¯¯¯¯AC=3¯¯¯¯¯¯CB, then 2¯¯¯¯¯¯OA+3¯¯¯¯¯¯OB=
View Solution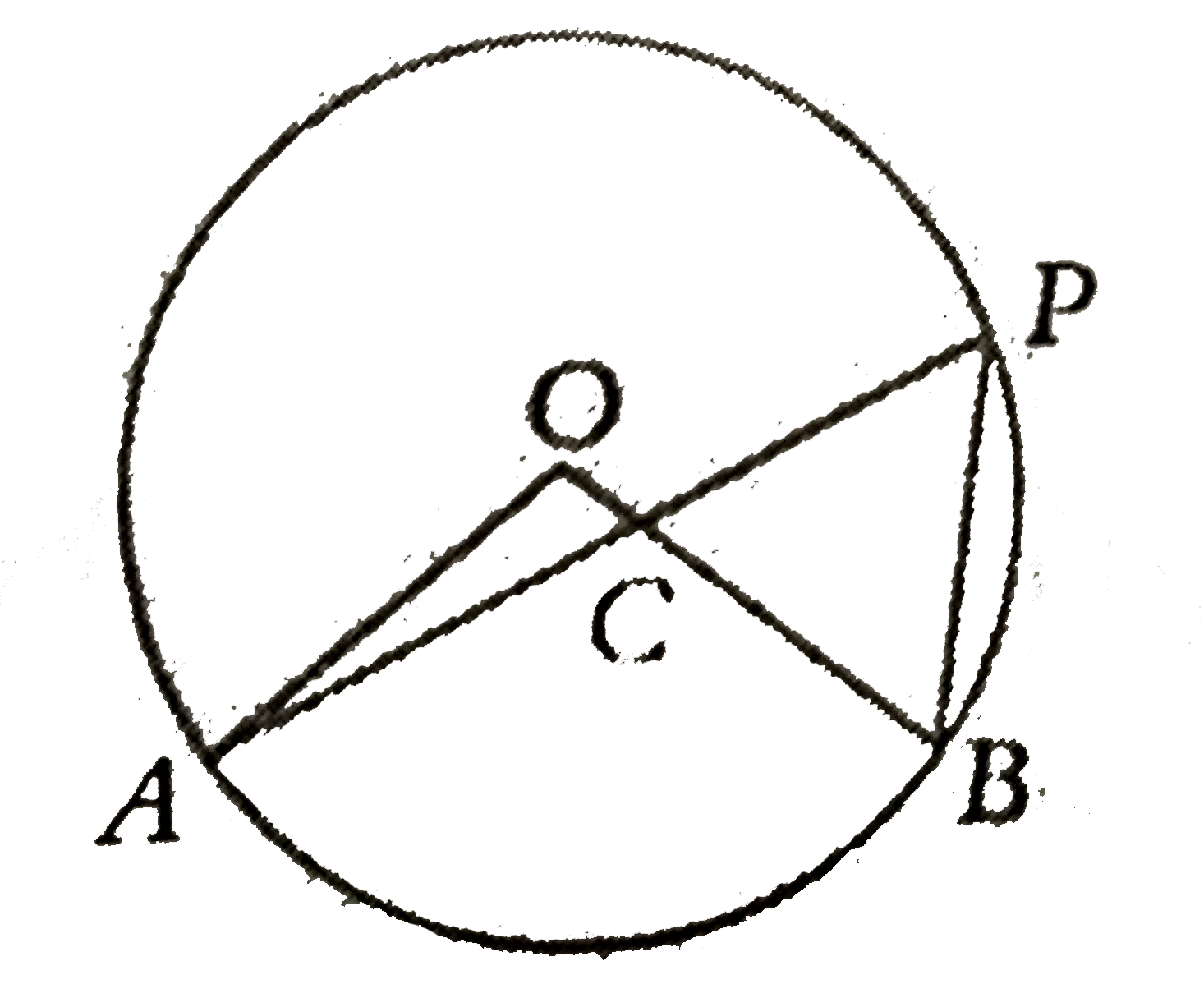
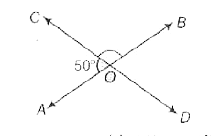
In the above figure (not to scale), O is the centre of the circle. ¯¯¯¯¯¯AP and ¯¯¯¯¯¯BP are two chords. C is the point of intersection of ¯¯¯¯¯¯AP and ¯¯¯¯¯¯OB. If ∠OAC=30∘ and ∠PBC=80∘, then ∠AOB=View SolutionTwo lines ¯¯¯¯¯¯AB and ¯¯¯¯¯¯CD cut each other at O. If ∠AOC=50∘, than ∠BOC is equal to
 View Solution
View Solution