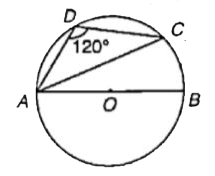
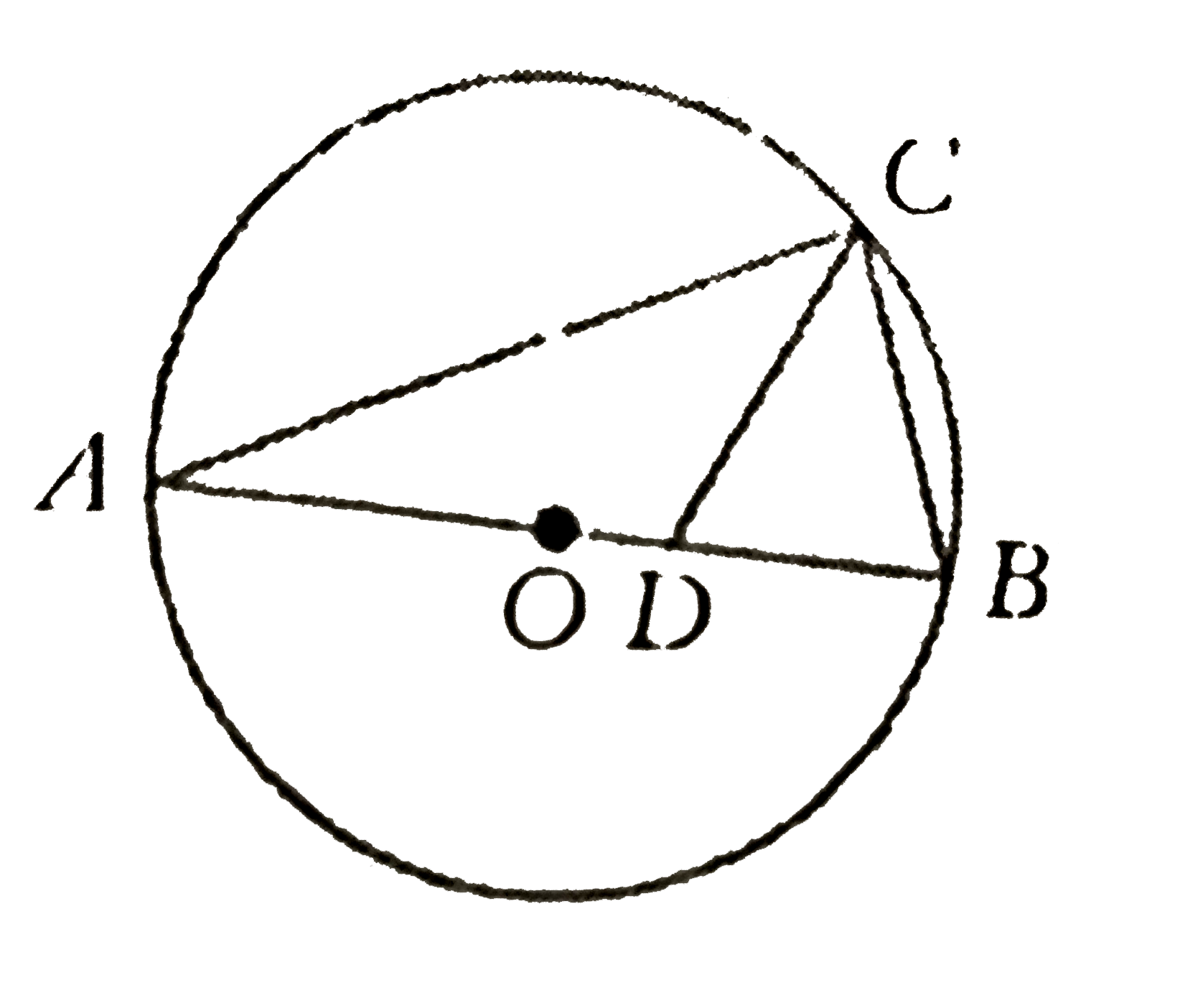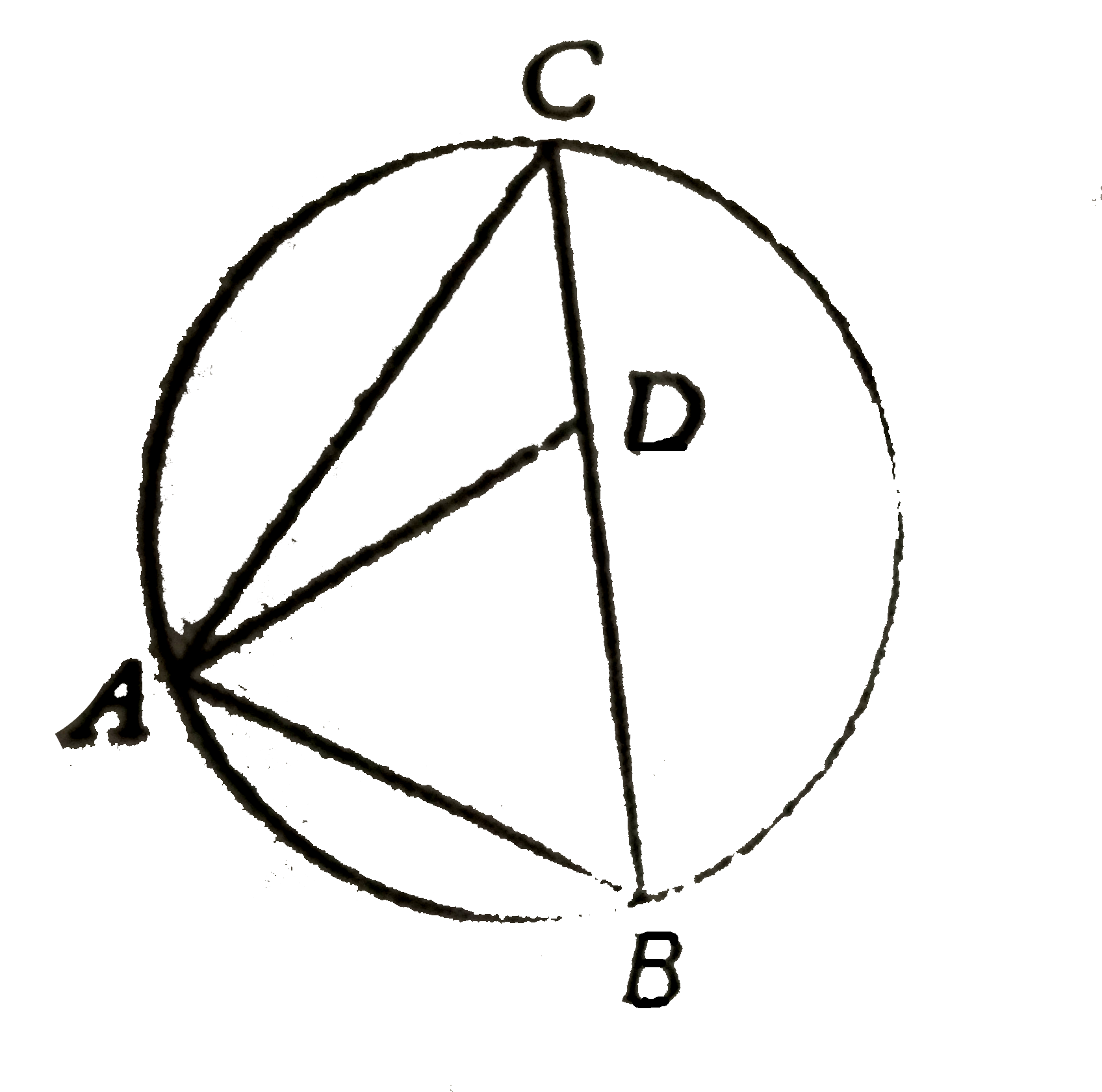 In the given figure, ∠DBA=2∠DAB=4∠CAD.
In the given figure, ∠DBA=2∠DAB=4∠CAD.
If ∠ADC=120∘ , then the angle made by AB at the centre of the circle is
A
20∘
B
40∘
C
60∘
D
80∘
Video Solution
Text Solution
The correct Answer is:d
(i) Consider ∠CAD as x, then ∠DAB=2x and ∠DBA=4x, using these angles and find ∠ACB.
(ii) Angle made by arc AB at the centre of the circle =2∠ACB.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level 220videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level 37videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Essay type Question3videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FormulaeEXERCISE - Level 37videos
Formulae
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICESEXERCISE - CONCEPT APPLICATION (Level 3)7videos
INDICES
Similar Questions
Knowledge Check
- Question 1 - Select One
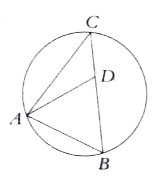
In the given figure , ∠DBA=2∠DAB=4∠CAD. If ∠ADC=120∘ , then the angle made by AB at the centre of the circle is _______.A20∘B40∘C60∘D80∘ - Question 2 - Select One

In the above figure, O is the centre of the circle and AB=CD. If ∠APB=110∘, then find the angle made by the chord CD at the centre.A220∘B110∘C120∘D140∘ - Question 3 - Select One
If O is the centre of the circle then find ∠ADC
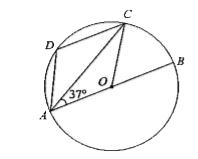 A125∘B127∘C90∘D137∘
A125∘B127∘C90∘D137∘

In the above figure, O is the centre of the circle and AB=CD. If ∠APB=110∘, then find the angle made by the chord CD at the centre.View Solution
In the above figure, ABCD is a cyclic quadrilateral and ∠BCD=2∠BAD. Find the angle made by the diagonal BD at the centre of the circle.View SolutionIn the given figure, AB is the diameter of the circle. ∠ADC=120∘. Find ∠CAB :
 View Solution
View SolutionIn the given figure, AOB is a diameter of a circle and CD||AB. If ∠BAD=30∘, then ∠CAD = ?
 View Solution
View SolutionIn the given figure, AB is the diameter of the circle, ∠ADC=120∘. Find ∠CAB:
 View Solution
View Solution