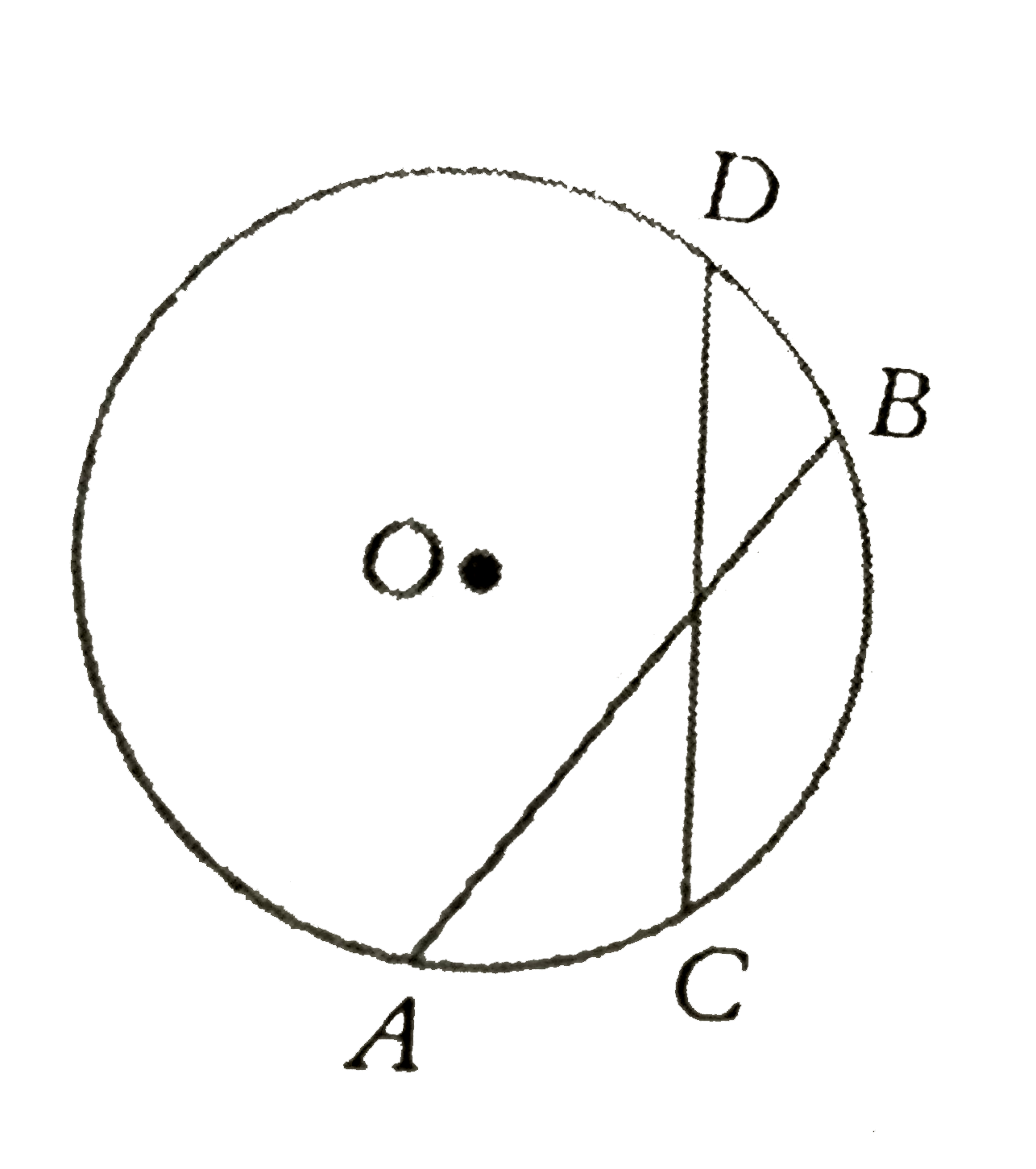
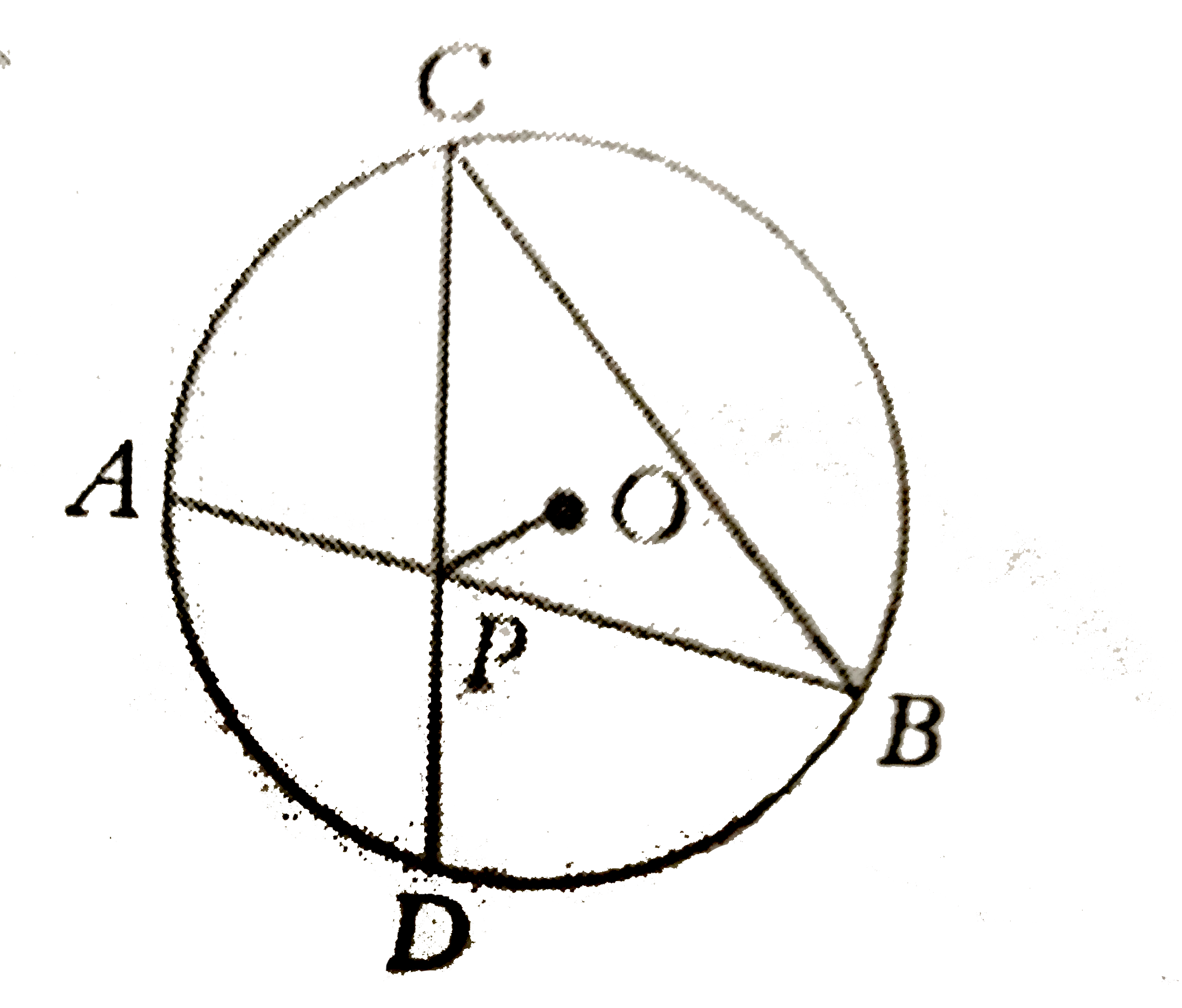 In the above figure , AB and CD are equal chords and O is the centre of the circle. If ∠OPB=50∘, then ∠PBD=____________
In the above figure , AB and CD are equal chords and O is the centre of the circle. If ∠OPB=50∘, then ∠PBD=____________
30∘
40∘
50∘
60∘
The correct Answer is:b
(i) Extend PO to cut the chord BC at sa M.
(ii) In ΔPMB=90∘ and given ∠OPB=50∘. Using this find ∠PBC
Topper's Solved these Questions
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level 2
20 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level 3
7 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Essay type Question
3 Videos
- FormulaeBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FormulaeEXERCISE - Level 3
7 Videos
- INDICESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICESEXERCISE - CONCEPT APPLICATION (Level 3)
7 Videos
Similar Questions
Knowledge Check
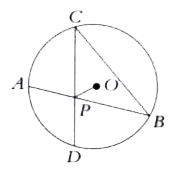
In the above figure , AB and CD are equal chords and O is the centre of the circle . If ∠OPB=50∘, then ∠PBC= ______ .A30∘B40∘C50∘D60∘
In the given figure,AB and CDare equal chords of a circle with centre O .Prove that ∠AOB≅∠COD and ∠AOB=∠COD
View Solution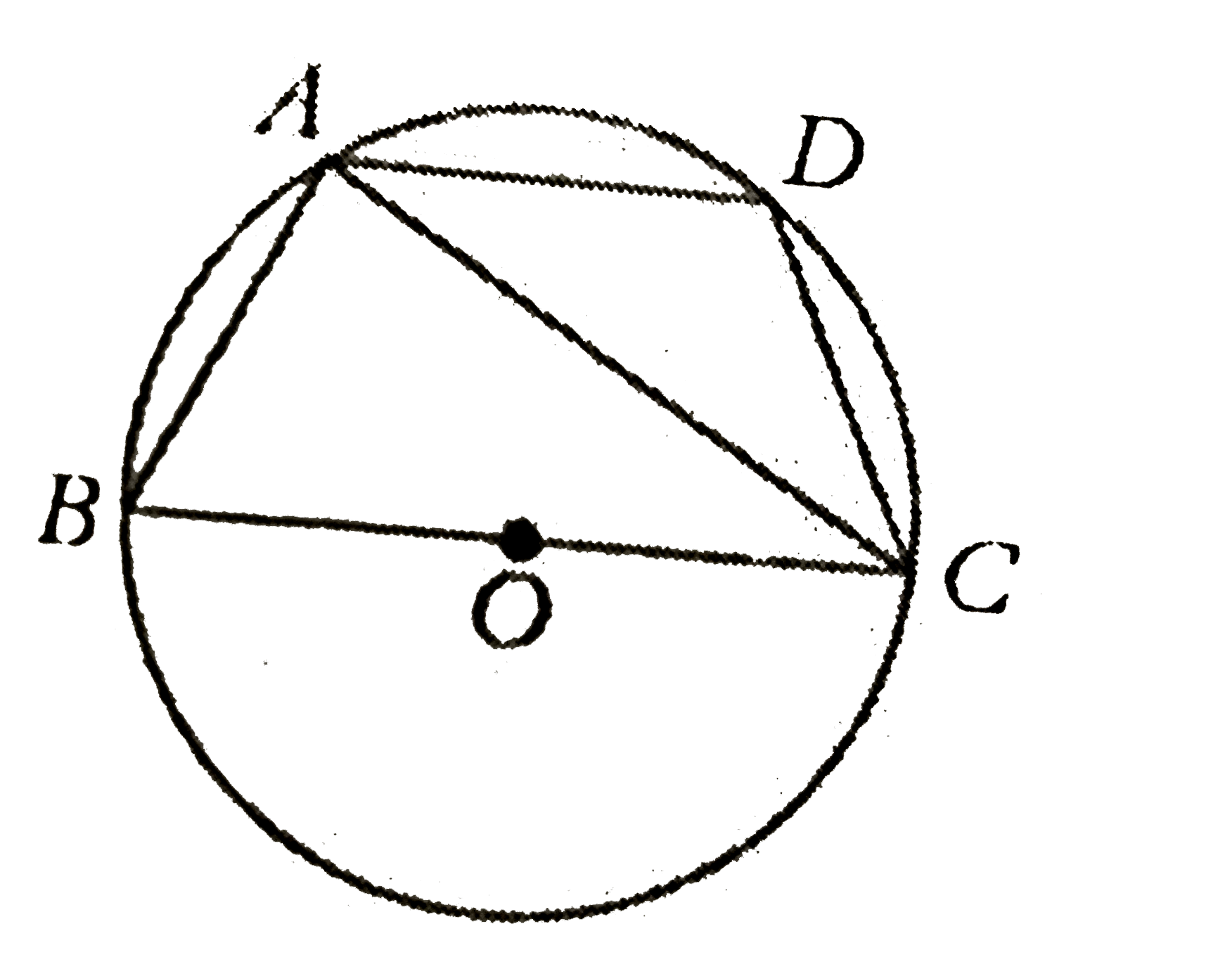
In the above figure, O is the centre of the circle AB,AD and CD are the chords . If ∠ADC=130∘ then fid ∠ACB.
View SolutionIn the adjoining figure, O is the centre of the circle. AB and CD are equal chords.
If ∠AOB=100∘, then find ∠CED.
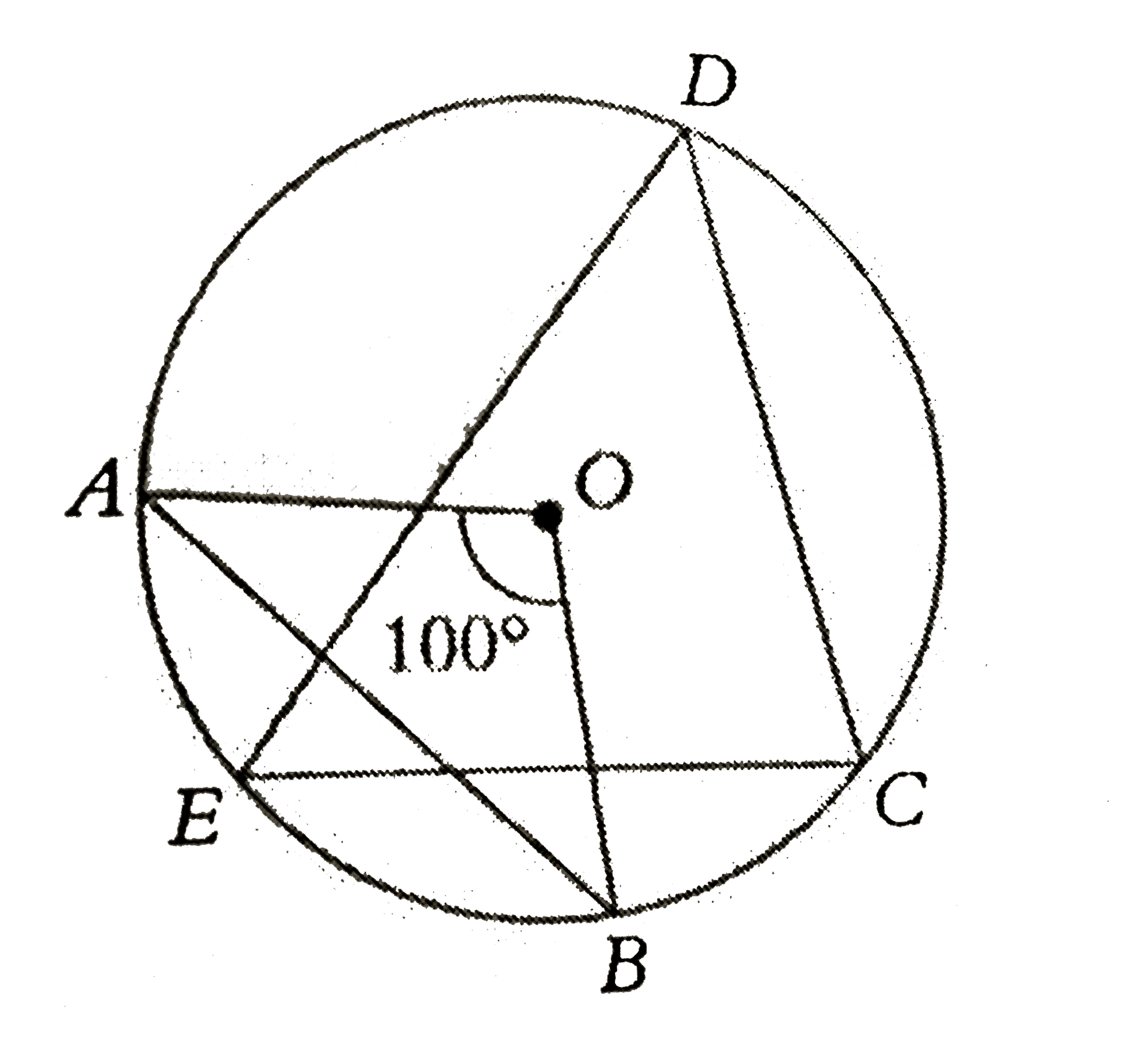
View SolutionIn the given figure,AB and BC are two chords of the circle with Centre O ,where ∠BAO=50∘,∠BCO=35∘,then ∠AOC is equal to
View SolutionIn the given figure, AB and AC are two equal chords of a circle with centre O. Show that O lies on the bisectors of ∠BAC.
View SolutionAB and CD are diameters of a circle with centre O. If ∠OBD=50∘, find ∠AOC
View Solution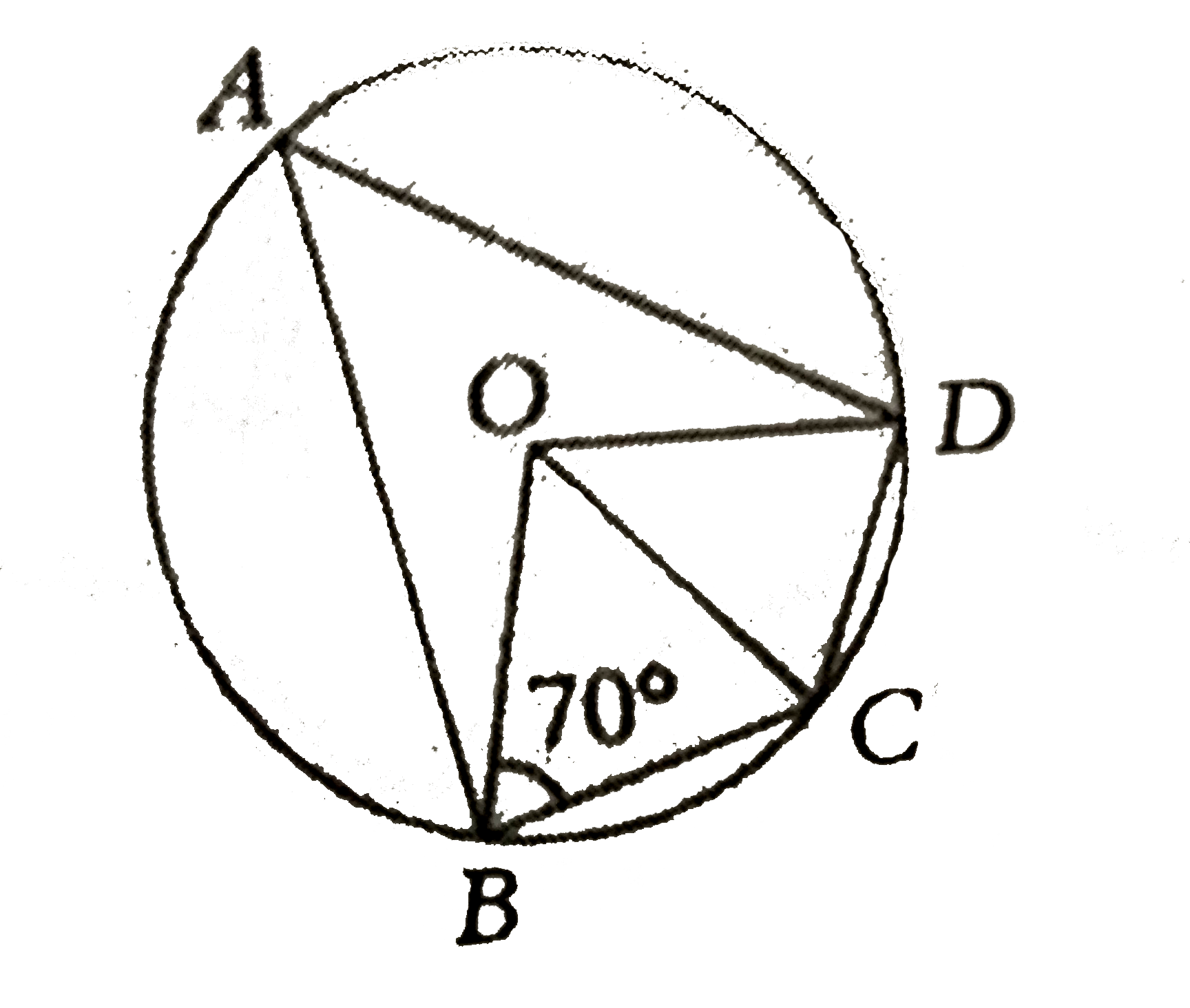
In the above figure (not to scale), O is the centre of the circle. ¯¯¯¯¯¯BC and ¯¯¯¯¯¯CD are equal chords. If ∠OBC=70∘ , then find ∠BAD.
View Solution