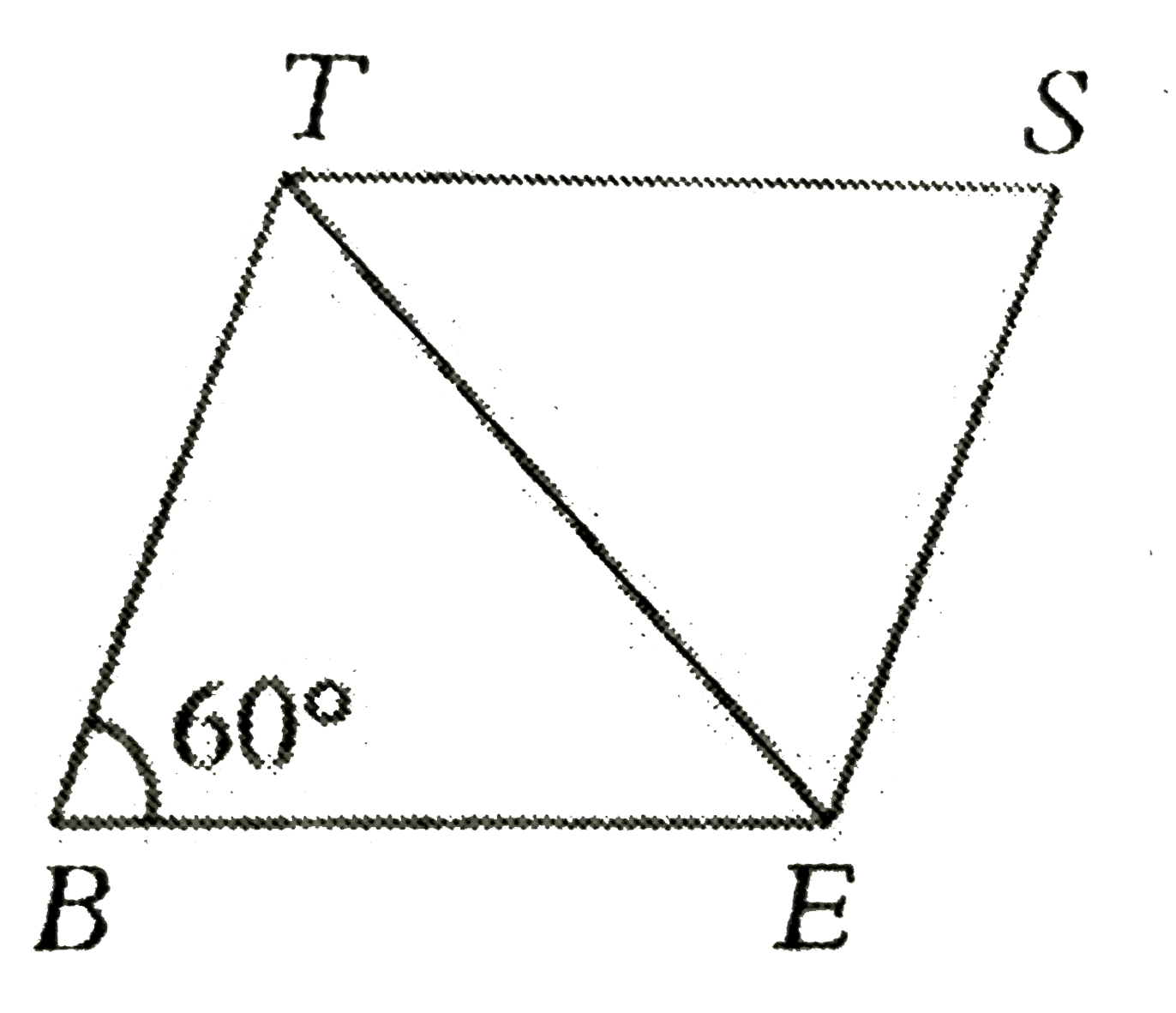
In a rhombus BEST,if / B=60^(@) and BT =6cm, then find the length of the diagonal TE. The following are the steps involved in solving the above problem. Arrange them in sequential order. (A) implies Delta BTE is an equilateral triangle. (B) Join T and E (C ) In Delta BET, BT=BE implies / BTE =/ BET =(180^(@)-60^(@))/(2)=60^(@) ( :' / B=60^(@)) . (D) TE=6 cm
In a rhombus BEST,if ∠B=60∘ and BT=6cm, then find the length of the diagonal TE.
The following are the steps involved in solving the above problem. Arrange them in sequential order.
(A) ⇒Δ BTE is an equilateral triangle.
(B) Join T and E
(C ) In ΔBET,BT=BE⇒∠BTE=∠BET=180∘−60∘2=60∘(∵∠B=60∘) .
(D) TE=6cm

A

BCAD

B

BCDA

C

BACD

D

BADC

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

(B),(C ) ,(A) and (D) is the required sequential order.

Updated on:21/07/2023
|
Class 8MATHSPRACTICAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • ocr_image
    In a rhombus BEST,if ∠B=60∘ and BT=6cm, then find the length of the diagonal TE.
    The following are the steps involved in solving the above problem. Arrange them in sequential order.
    (A) ⇒Δ BTE is an equilateral triangle.
    (B) Join T and E
    (C ) In ΔBET,BT=BE⇒∠BTE=∠BET=180∘−60∘2=60∘(∵∠B=60∘) .
    (D) TE=6cm

    ABCAD
    BBCDA
    CBACD
    DBADC

  • If 169 =b2+25 then find the value of b .The following sentences are the steps involved in solving the above problem .Arrange them in sequential order from the first to the last

    ABAC
    BBCA
    CCAB
    DACB

  • If tan(A+B)=1andA(−B)=1√2, then find A and B.
    The following are the steps involved in solving the above problem. Arrange them in sequential order.
    (A) tan(A+B)=1⇒tan(A+B)=tan45∘andsin(A−B)=1√2⇒sin(A−B)=sin45∘.
    (B) 2A=90∘⇒A=45∘.
    (C ) A+B=45∘andA−B=45∘.
    (D) ∴A=45∘andB=0∘.

    ADBCA
    BCABD
    CACDB
    DACBD