A 20 Henry inductor coil is connected to a 10 ohm resistance in series as shown in figure . The time at which rate of dissipation of energy (joul's heat ) across resistance is equal to the rate at which magnetic energy is strored in the inductor , is

2In2
In 2
12 In2
2In 2
The correct Answer is:D
(d) Energy stored in the inductor is given by
U=1Li2⇒dUdt=12L×2i×didt=Lididt
It is given that
dUdt=i2R⇒Lididt=i2R
⇒Ldidt=iR
Current in the LR circuit is given by
i=ER(1−e−RtL)⇒didt=ER×RLe−RtL=ELe−RtL
Substituting values in equation (i) we get
L×ERe−RtL=ER(1−e−RtL)R⇒e−RtL=1−e−RtL
eRtL=2⇒t=LRIn2
⇒t=2010In 2=2In2
Hence option (d) is correct.
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - COMPETITION FILE JEE (ADVANCED ) FOR IIT ENTRANCE
4 Videos
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - COMPETITION FILE C. MULTIPLE CHOICE QUESTIONS
17 Videos
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS) B. MULTIPLE CHOICE QUESTIONS
15 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
Similar Questions
A 20 Henry inductor coil is connected to a 10ohm resistance in series as shown in figure. The time at which rate of dissipation of energy (Joule's heat) across resistance is equal to the rate at which magnetic energy is stored in the inductor, is:
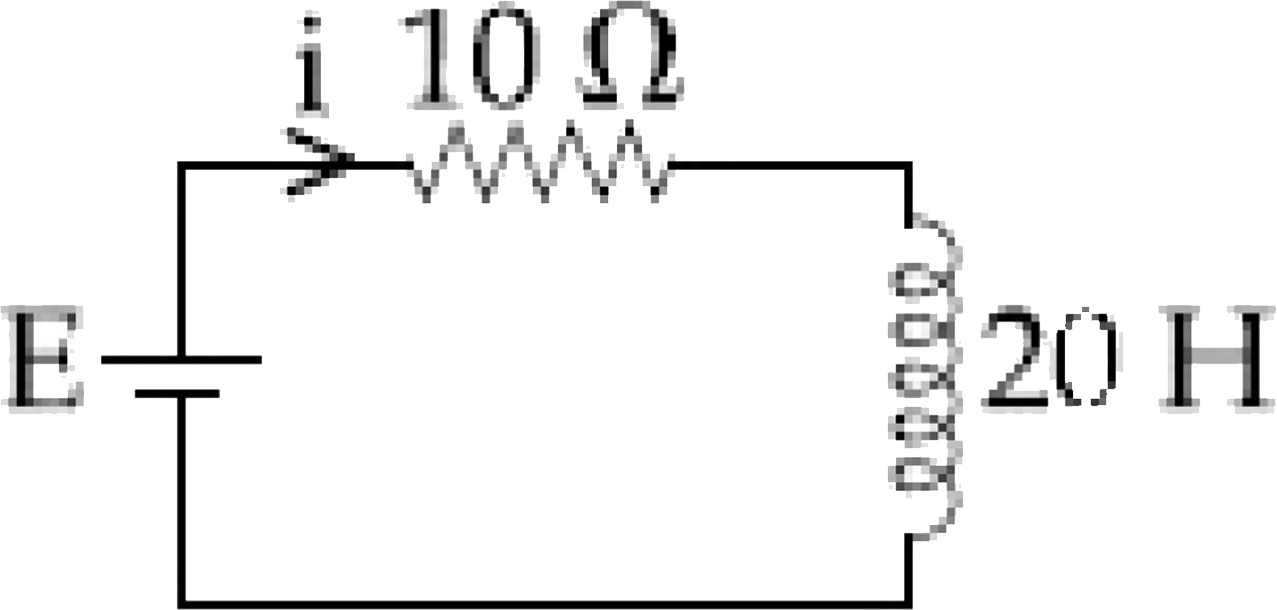
View SolutionThe switch is closed at t=0. The time after which the rate of dissipation for energy in the resistor is equal to rate at which energy is being stored in the inductor is : (A) ln2 (B) 12ln2 (C) 14ln2 (D) 2ln2
View Solution
Knowledge Check
An inductor of 5 henry and a resistance of 20 ohm are connected in series with a battery of 5 volt. The initial rate of change of current is
A1As−1B2.0As−1C2.5As−1D0.25As−1An inductor of 2 henry and a resistance of 10 ohms are connected in series with a battery of 5 volts. The initial rate of change of current is
A0.5amp/secB2.0amp/secC2.5amp/secD0.25amp/secA capacitor is connected across an inductor. At time t = 0 charge on the capacitor is equal to 1√2qmax, where qmax is the maximum charge on the capacitor. The time t, at which the energy stored in the capacitor is equal to the energy stored in the inductor is (The inductance of the inductor is L and capacitance of the capacitor is C. Resistance of the circuit is zero)
A2π√LCB12π√LCCπ√LC2D12π√LC
An inductor of self-inductance L and resistor of resistance R are connected in series to a battery of emf E and negligible resistance.Calculate the maximum rate at which energy is stored in the inductor.
View SolutionAn inductor coil is connected to an source through a 60Ω resistance in series. The source voltage, voltage across the coil and voltage across the resistance are found to be 33V, 27V and 12V respectively. The resistance of the coil is
A. 30Ω
B. 45Ω
C. 105Ω
D. 75Ω
View SolutionA coil of inductance 1H and resistance 10Ω is connected to a resistanceless battery of emf 50V at time t=0. Calculate the ratio of rthe rate which magnetic energy is stored in the coil to the rate at which energy is supplied by the battery at t=0.1s.
View SolutionA coil of inductance 1H and resistance 10Ω is connected to a resistanceless battery of emf 50V at time t=0. Calculate the ratio of rthe rate which magnetic energy is stored in the coil to the rate at which energy is supplied by the battery at t=0.1s.
View Solution5A 50 mH inductor is in series with a 10 2 resistor and a battery with an emf oj 25 V. At t = 0 the switch is closed. Find
Q(c) the rate at which energy is stored in the inductor,
View Solution
