The area bounded by y=x2,y=[x+1],0≤x≤2 and the y-axis is where [.] is greatest integer function.
A
13
B
√23
C
1
D
73
Video Solution
Text Solution
The correct Answer is:B
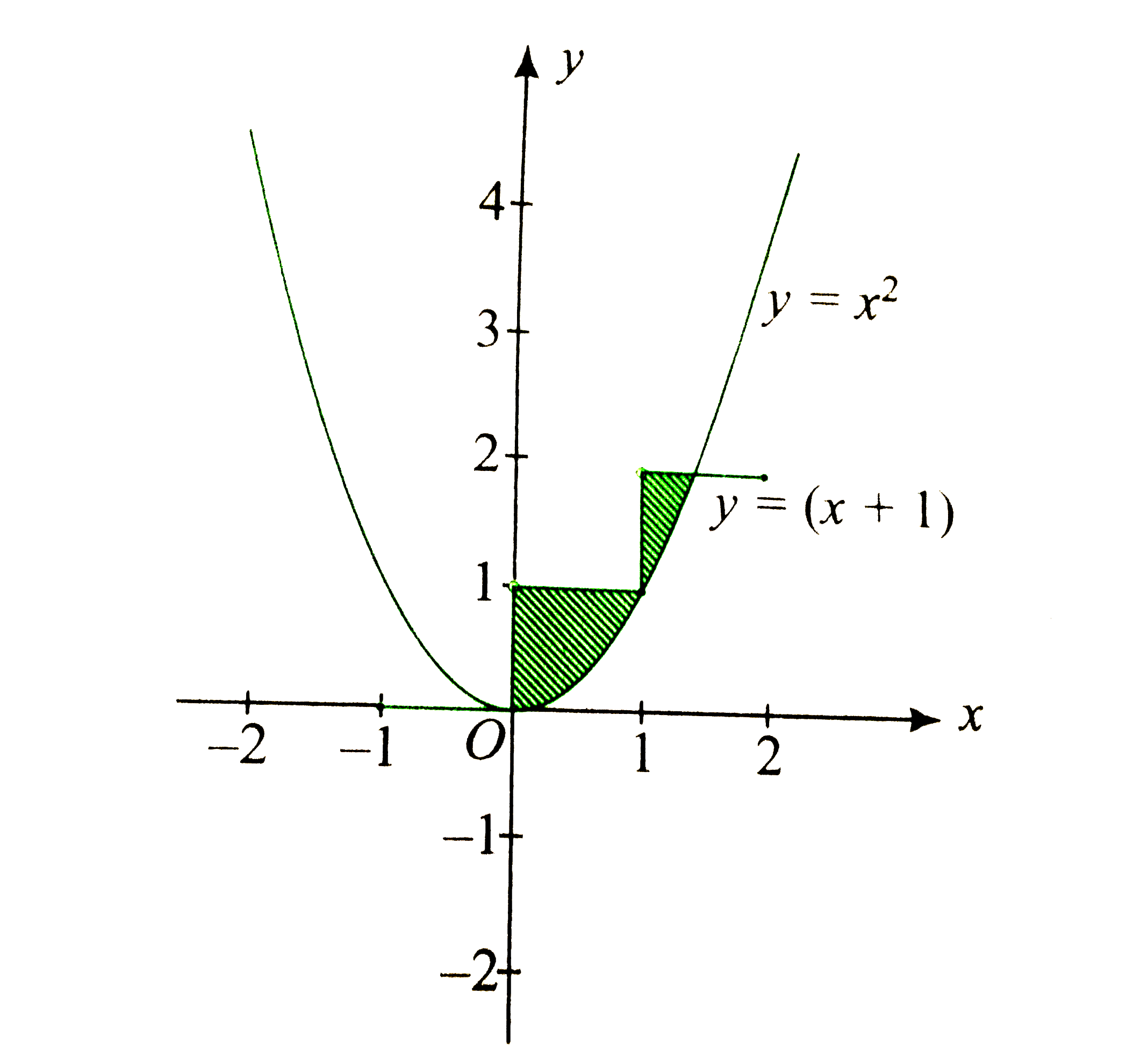
Area 1∫0(1−x2)dx+√2∫1(1−x2)dx=[x−x33]10+[x−x33]√21
=√23
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Multiple)10videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Comprehension)21videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.37videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank29videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank20videos
AREA UNDER CURVES
Similar Questions
Knowledge Check
- Question 1 - Select One
The area bounded by y=x2,y=√x,0≤x≤4 is
A203B103C10D503 - Question 2 - Select One
The area of region between y=4−x2,0≤x≤2 and the x-axis is
A43B73C163D53 - Question 3 - Select One
The area between y = x and y=x2,0≤x≤2 is
A1B23C13D43
Area of the region bounded by [x]2=[y]2 ,if x∈[1,3] (where [ .] denotes the greatest integer function),is less than
View SolutionThe area bounded by f(x)=x2,0≤x≤1,g(x)=−x+2,1≤x≤2 and x- axis is
View SolutionLet 'c' be a positive real number such that area bounded by y=0,y=[tan−1x] from x=0 to x=c is equal to area bounded by y=0,y=[cot−1x], from x=0 to x=c (where [⋆] represents greatest integer function), then
View SolutionThe area (in sq. units) bounded by [|x|]+[|y|]=2 in the first and third quardant is (where [.] is the greatest integer function).
View SolutionArea bounded by the curve y=logex,x=0,y≤0 and x-axis is:
View Solution

