Area bounded by $y = {sec}^{- 1} x$ , $y = {cot}^{- 1} x$ and line x=1 is given by

A

$log (3 + 2 \sqrt{2}) - \frac{π}{2}$ sq. units

B

$\frac{π}{2} - log (3 + 2 \sqrt{2})$ sq. units

C

$π - {log}_{e} 3$ sq. units

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

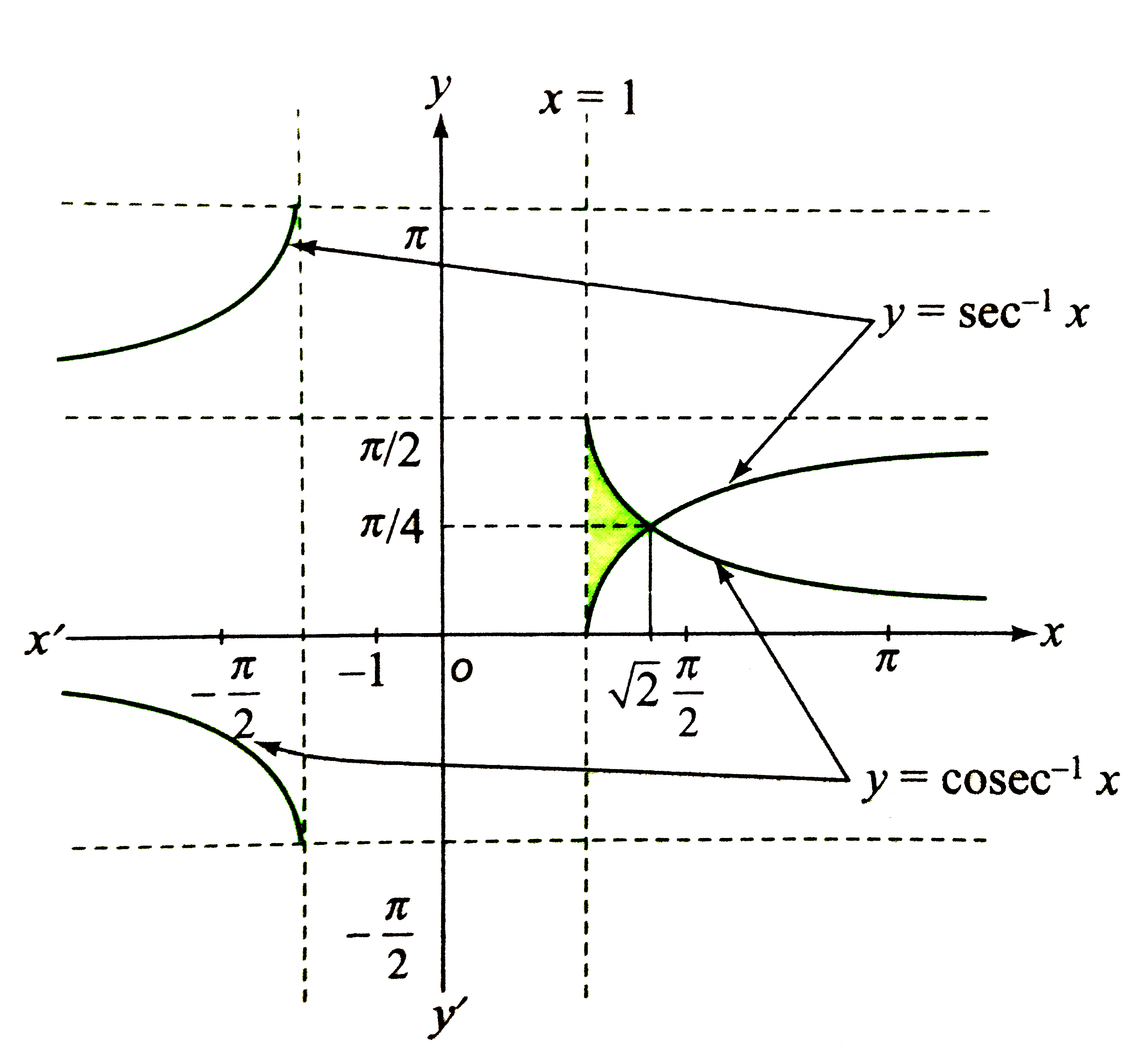
Integrating along x-axis, we get
$A = \sqrt{2} \int 1 (cos e c^{- 1} x - {sec}^{- 1} x) d x$
Integrating along y-axis, we get
$A = 2 π / 6 \int 0 (sec y - 1) d y$
$= 2 {[log | sec y + tan y | - y]}_{0}^{π / 4}$
$= 2 [log ∣ ∣ \sqrt{2} + 1 ∣ ∣ - \frac{π}{2}]$
$= log (3 + 2 \sqrt{2}) - \frac{π}{2}$ sq. units.

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The area of the closed region bounded by $y = {sec}^{- 1} x, y = {cosec}^{- 1} x$ and the line $x - 1 = 0$ is
A ${{log}_{e} (3 + 2 \sqrt{2}) - \frac{π}{2}} sq. units$
B ${\frac{π}{2} - {log}_{e} (3 + 2 \sqrt{2})} sq. units$
C $π - 3 {log}_{e} 3 sq. units$
DNone of these
Question 2 - Select One
Area bounded by $y = {tan}^{- 1} x, y = {cot}^{- 1} x$ and y-axis is equal to
Aln $\sqrt{2}$ sq. unit
Bln 4 sq. unit
Cln 8 sq. unit
Dln 2 sq. unit
Question 3 - Select One
The area bounded by the curve $| x | + | y | = 1$ and axis of x, is given by
A2sq unit
B1 sq unit
C4 sq unit
DNone of these

CENGAGE-AREA-Exercise (Single)

Home
Ask Doubt
Profile